Dreisatz: Probleme lösen leicht gemacht

16 Oct 2024
de
Emil

Wie berechnet man eigentlich, wie viel Mehl man für ein doppelt so großes Rezept benötigt? Oder wie lange braucht man für eine Strecke, wenn man die Geschwindigkeit ändert? Die Antwort auf diese und viele ähnliche Fragen liefert der Dreisatz.

Der Dreisatz, auch bekannt als "regra de 3 com 3 elementos" im Portugiesischen, ist eine einfache, aber effektive Methode, um Proportionalitätsprobleme zu lösen. Er basiert auf der Logik, dass sich bei Änderung einer Größe eine andere Größe im gleichen Verhältnis ändert.

Im Alltag begegnen uns ständig Situationen, in denen der Dreisatz hilfreich ist. Vom Kochen und Backen über die Berechnung von Fahrtzeiten und -kosten bis hin zur Dosierung von Medikamenten – die Anwendungsmöglichkeiten sind vielfältig.

Die Methode des Dreisatzes ist nicht nur im Alltag nützlich, sondern auch in vielen Berufsfeldern unverzichtbar. Ingenieure, Wissenschaftler, Kaufleute und viele andere nutzen ihn regelmäßig, um komplexe Berechnungen durchzuführen.

Dieses Wissen über den Dreisatz, dieses praktische Werkzeug, das uns im Alltag und im Beruf so viele Vorteile bietet, ist leicht zu erlernen und anzuwenden. Im Folgenden werden wir die Grundlagen, Anwendungsmöglichkeiten und Beispiele des Dreisatzes genauer betrachten.

Die Geschichte des Dreisatzes reicht weit zurück. Bereits in alten Kulturen wurde er zur Lösung von Proportionalitätsproblemen verwendet. Die genaue Herkunft ist schwer zu bestimmen, aber es ist bekannt, dass er schon in der Antike Anwendung fand. Ein zentrales Problem im Zusammenhang mit dem Dreisatz ist die korrekte Identifizierung der proportionalen Beziehungen. Es ist wichtig zu verstehen, welche Größen direkt und welche indirekt proportional zueinander sind.

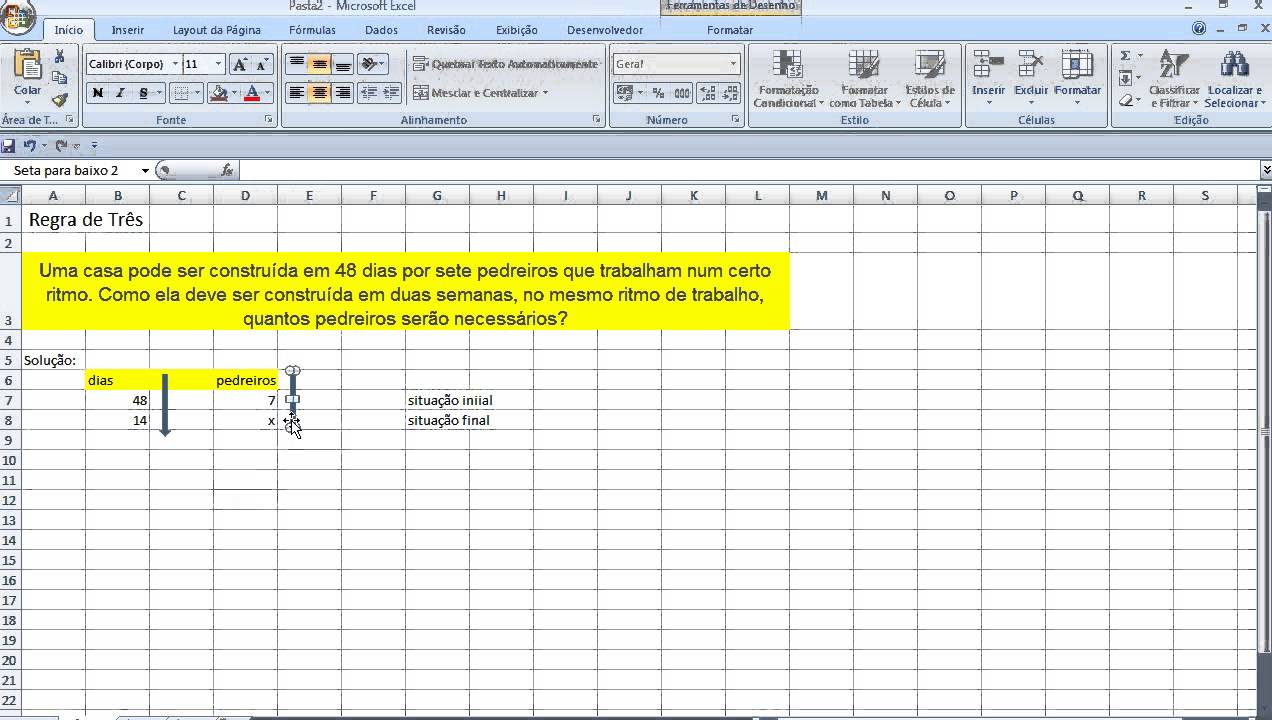
Der Dreisatz basiert auf der Beziehung zwischen drei gegebenen Werten und einem gesuchten Wert. Man stellt die Werte in einer Tabelle dar und berechnet den gesuchten Wert durch Kreuzmultiplikation und Division. Ein einfaches Beispiel: Wenn 3 Äpfel 2 Euro kosten, wie viel kosten 6 Äpfel? Die Lösung: (6 Äpfel * 2 Euro) / 3 Äpfel = 4 Euro.

Vorteile des Dreisatzes:

1. Einfachheit: Die Methode ist leicht zu verstehen und anzuwenden.

2. Effizienz: Der Dreisatz ermöglicht eine schnelle Lösung von Proportionalitätsproblemen.

3. Vielseitigkeit: Er ist in vielen Bereichen des Alltags und Berufslebens anwendbar.

Aktionsplan: 1. Identifizieren Sie die drei gegebenen Werte und den gesuchten Wert. 2. Stellen Sie die Werte in einer Tabelle dar. 3. Berechnen Sie den gesuchten Wert durch Kreuzmultiplikation und Division.

Häufig gestellte Fragen:

1. Was ist der Dreisatz? 2. Wie funktioniert der Dreisatz? 3. Wann kann man den Dreisatz anwenden? 4. Was ist der Unterschied zwischen direkter und indirekter Proportionalität? 5. Gibt es Online-Rechner für den Dreisatz? 6. Wo finde ich Übungsaufgaben zum Dreisatz? 7. Wie kann ich den Dreisatz im Alltag nutzen? 8. Welche Fehler sollte man beim Dreisatz vermeiden?

Tipps und Tricks: Achten Sie auf die Einheiten der Größen. Stellen Sie sicher, dass die proportionalen Beziehungen korrekt identifiziert sind. Üben Sie den Dreisatz mit verschiedenen Beispielen.

Zusammenfassend lässt sich sagen, dass der Dreisatz ein mächtiges Werkzeug zur Lösung von Proportionalitätsproblemen ist. Er ist einfach zu erlernen, effizient in der Anwendung und vielseitig einsetzbar. Von alltäglichen Berechnungen bis hin zu komplexen Aufgaben im Berufsleben – der Dreisatz bietet eine effektive Methode, um schnell und präzise Ergebnisse zu erzielen. Nutzen Sie die Vorteile des Dreisatzes und vereinfachen Sie Ihre Berechnungen. Die Fähigkeit, den Dreisatz anzuwenden, ist eine wertvolle Kompetenz, die in vielen Lebensbereichen von Nutzen sein kann. Machen Sie sich mit dieser Methode vertraut und profitieren Sie von ihrer Einfachheit und Effizienz. Durch Übung und Anwendung werden Sie schnell die verschiedenen Möglichkeiten des Dreisatzes meistern und ihn zu Ihrem Vorteil nutzen können.