Stell dir vor, du könntest gleichzeitig die genaue Position und Geschwindigkeit eines winzigen Elektrons bestimmen. Klingt einfach, oder? In der Welt der Quantenphysik ist dies jedoch unmöglich – dank der Heisenbergschen Unschärferelation. Aber was genau bedeutet diese Theorie, die unser klassisches Weltbild auf den Kopf stellt?
Die Heisenbergsche Unschärferelation, formuliert von Werner Heisenberg im Jahr 1927, besagt, dass wir bestimmte Paare von physikalischen Eigenschaften eines Teilchens, wie beispielsweise seinen Ort und seinen Impuls (Masse mal Geschwindigkeit), nicht gleichzeitig beliebig genau messen können. Je genauer wir den einen Wert bestimmen, desto ungenauer wird die Messung des anderen Wertes.
Diese Unschärfe liegt nicht an unseren Messinstrumenten, sondern ist eine fundamentale Eigenschaft der Quantenwelt. Das bedeutet, dass die Teilchen nicht gleichzeitig einen definierten Ort und Impuls besitzen, wie wir es aus unserer makroskopischen Welt gewohnt sind. Vielmehr existieren sie in einem Zustand der Wahrscheinlichkeit, in dem Ort und Impuls "verschmiert" sind.
Ein anschauliches Beispiel dafür ist das Elektron in einem Atom. Wir können nicht sagen, wo sich das Elektron zu einem bestimmten Zeitpunkt genau befindet, sondern nur, mit welcher Wahrscheinlichkeit es sich an einem bestimmten Ort aufhält. Diese Wahrscheinlichkeit wird durch Orbitale beschrieben, die Bereiche um den Atomkern darstellen, in denen sich das Elektron mit hoher Wahrscheinlichkeit aufhält.
Die Heisenbergsche Unschärferelation hat weitreichende Konsequenzen für unser Verständnis der Welt. Sie zeigt uns die Grenzen unserer klassischen Vorstellungskraft auf und zwingt uns, die Welt der Quantenmechanik mit ihren ungewohnten Gesetzmäßigkeiten zu akzeptieren. Sie ist zudem die Grundlage für viele technologische Entwicklungen, wie z.B. den Laser oder die moderne Elektronik.
Vorteile der Heisenbergschen Unschärferelation
Obwohl die Unschärferelation zunächst unsere klassischen Intuitionen herausfordert, bietet sie auch einige interessante Vorteile:
- Existenz von Atomen: Ohne die Unschärferelation würden Atome kollabieren. Da Elektronen nicht gleichzeitig einen definierten Ort und Impuls haben können, fallen sie nicht in den Kern, sondern bewegen sich in einem bestimmten Abstand darum herum.
- Tunneleffekt: Die Unschärfe erlaubt es Teilchen, scheinbar unüberwindbare Energiebarrieren zu durchtunneln. Dies ist beispielsweise die Grundlage für den radioaktiven Zerfall und für die Funktionsweise von Transistoren.
- Quantencomputer: Die Prinzipien der Quantenmechanik, einschließlich der Unschärferelation, ermöglichen die Entwicklung von Quantencomputern. Diese neuartigen Computer könnten bestimmte Aufgaben um ein Vielfaches schneller lösen als klassische Computer.
Häufige Fragen zur Heisenbergschen Unschärferelation
Hier sind einige der häufigsten Fragen und Antworten zur Heisenbergschen Unschärferelation:
- Gilt die Unschärferelation nur für Quantenobjekte?
Ja, die Unschärferelation spielt in der makroskopischen Welt keine Rolle. Die Unschärfe ist so gering, dass sie im Alltag nicht messbar ist. - Widerspricht die Unschärferelation dem Determinismus?
Ja, die Unschärferelation stellt die klassische Vorstellung in Frage, dass alle Ereignisse durch vorherige Zustände eindeutig bestimmt sind. In der Quantenwelt regiert der Zufall. - Kann man die Unschärferelation umgehen?
Nein, die Unschärferelation ist eine fundamentale Eigenschaft der Natur. Es gibt keine Möglichkeit, sie zu umgehen oder zu überlisten.
Fazit
Die Heisenbergsche Unschärferelation mag zunächst verwirrend erscheinen, doch sie ist ein Schlüssel zum Verständnis der Quantenwelt. Sie zeigt uns die Grenzen unseres klassischen Weltbildes auf und zwingt uns, die Welt mit anderen Augen zu betrachten. Obwohl sie die präzise Vorhersage von Ereignissen auf Quantenebene unmöglich macht, eröffnet sie gleichzeitig neue Möglichkeiten und technologische Innovationen. Die Erforschung und Anwendung der Quantenmechanik, die auf dieser fundamentalen Theorie basiert, birgt ein enormes Potenzial für die Zukunft.
Heisenberg principle for dummies - Trees By Bike
Heisenberg uncertainty principle fourier transform - Trees By Bike
Heisenberg Uncertainty Principle Formula Sheet - Trees By Bike
heisenberg's uncertainty principle definition - Trees By Bike
heisenberg's uncertainty principle definition - Trees By Bike
heisenberg's uncertainty principle definition - Trees By Bike
heisenberg's uncertainty principle definition - Trees By Bike
Heisenberg uncertainty principle equation - Trees By Bike
heisenberg's uncertainty principle definition - Trees By Bike
heisenberg's uncertainty principle definition - Trees By Bike
Heisenberg's Uncertainty Principle And Borns Equation Presentation - Trees By Bike
Heisenberg principle for dummies - Trees By Bike
The Heisenberg Uncertainty Principle[1] - Trees By Bike
Heisenberg uncertainty principle definition - Trees By Bike
heisenberg's uncertainty principle definition - Trees By Bike


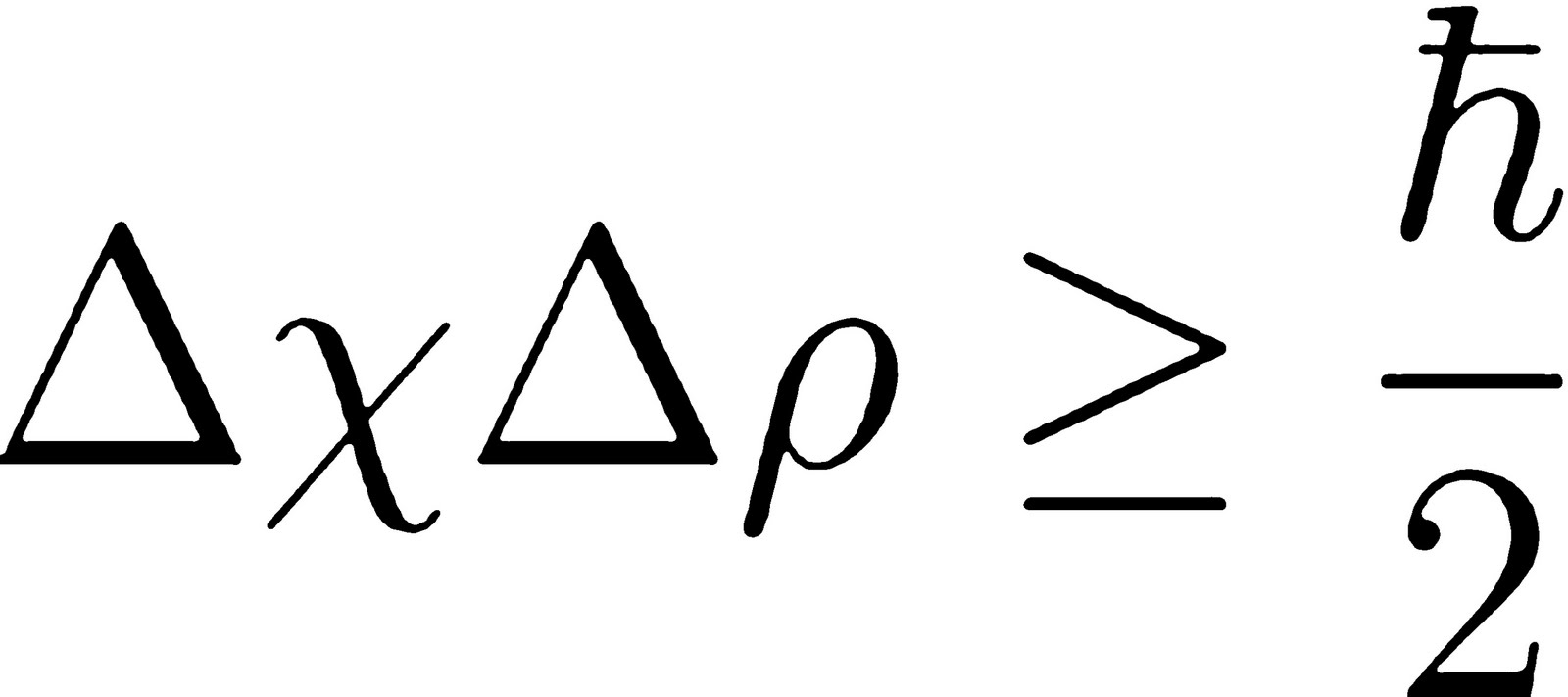









![The Heisenberg Uncertainty Principle[1]](https://i2.wp.com/image.slidesharecdn.com/theheisenberguncertaintyprinciple1-091020215730-phpapp01/95/the-heisenberg-uncertainty-principle1-2-1024.jpg?cb=1256075867)

