Heisenbergs Unschärferelation Formel: Die Grenzen der Gewissheit

25 Mar 2024
de
Emil

heisenberg's uncertainty principle formula

Stellen Sie sich vor, Sie versuchen, einen winzigen, sich schnell bewegenden Tennisball im Dunkeln zu orten. Sie benutzen eine Taschenlampe, um ihn zu finden, aber sobald das Licht auf den Ball trifft, verändert es seine Richtung und Geschwindigkeit. Dies ist eine Analogie zu dem, was in der Quantenwelt passiert, und es ist der Kern von Heisenbergs Unschärferelation.

Heisenbergs Unschärferelation, formuliert vom deutschen Physiker Werner Heisenberg im Jahr 1927, ist ein Grundprinzip der Quantenmechanik. Es besagt, dass wir niemals gleichzeitig den Ort und den Impuls (Masse mal Geschwindigkeit) eines Teilchens mit absoluter Genauigkeit kennen können. Je genauer wir den Ort messen, desto ungenauer wird unsere Messung seines Impulses und umgekehrt.

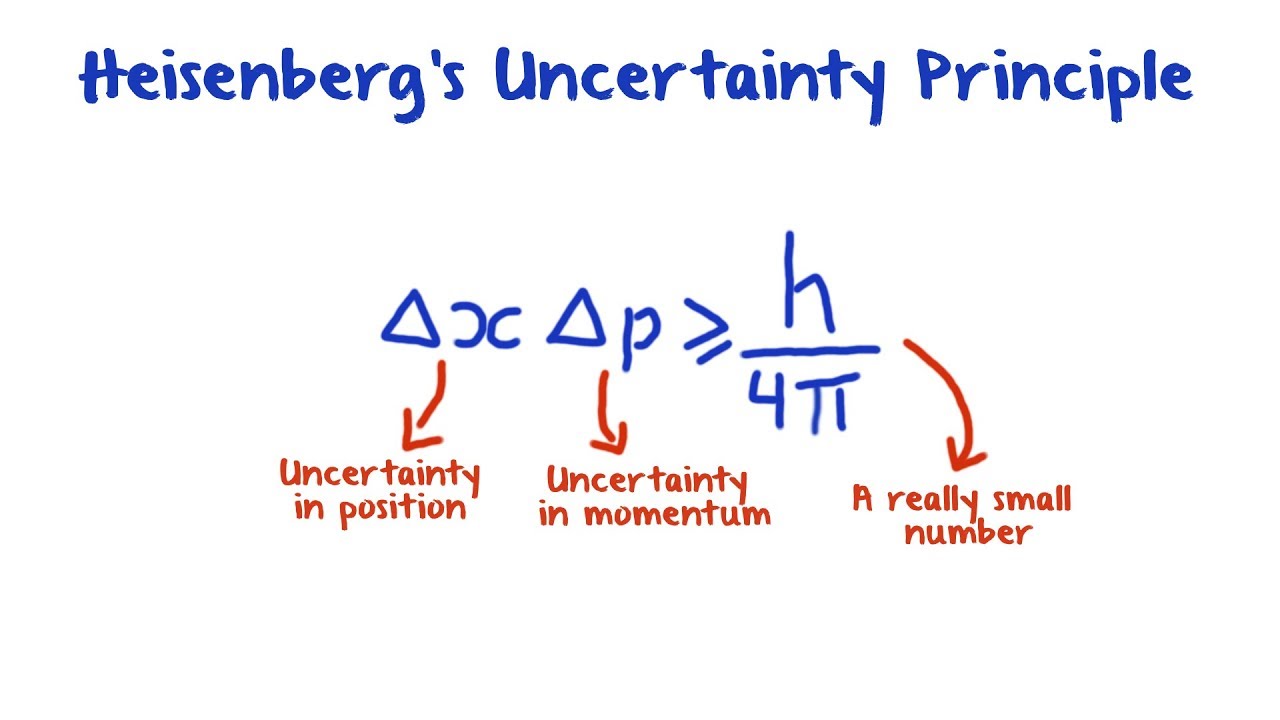
Die Unschärferelation wird oft durch die folgende Formel dargestellt: Δx * Δp ≥ h/4π. In dieser Formel steht Δx für die Unschärfe des Ortes, Δp für die Unschärfe des Impulses und h ist das Plancksche Wirkungsquantum, eine fundamentale Konstante in der Quantenmechanik. Die Formel zeigt, dass das Produkt der Unschärfen immer größer oder gleich einem bestimmten Wert sein muss, was bedeutet, dass es eine fundamentale Grenze für die Genauigkeit unserer Messungen gibt.

Diese Unschärfe ist nicht auf technische Einschränkungen unserer Messgeräte zurückzuführen, sondern eine inhärente Eigenschaft der Quantenwelt. Teilchen existieren nicht an einem bestimmten Ort mit einer bestimmten Geschwindigkeit, bis sie gemessen werden. Stattdessen werden sie durch eine Wellenfunktion beschrieben, die eine Wahrscheinlichkeitsverteilung ihrer möglichen Orte und Impulse angibt.

Heisenbergs Unschärferelation hat tiefgreifende Auswirkungen auf unser Verständnis der Welt. Sie stellt den Determinismus der klassischen Physik in Frage und führt das Konzept der Wahrscheinlichkeit in die Physik ein. Anstatt von Teilchen, die sich auf vorhersagbaren Bahnen bewegen, haben wir es in der Quantenwelt mit Wahrscheinlichkeitswellen und Unschärfe zu tun.

Vorteile der Unschärferelation

Obwohl die Unschärferelation oft als Einschränkung angesehen wird, bietet sie auch einzigartige Möglichkeiten:

Existenz von Atomen: Die Unschärferelation verhindert, dass Elektronen in den Atomkern stürzen, was die Stabilität von Atomen und damit aller Materie ermöglicht.
Tunneleffekt: Teilchen können dank der Unschärfe des Impulses Energiebarrieren "durchtunneln", was in vielen Bereichen wie der Kernfusion und der Elektronik Anwendung findet.
Quantencomputer: Die Prinzipien der Quantenmechanik, einschließlich der Unschärferelation, werden genutzt, um leistungsfähigere Computer zu entwickeln.

Beispiele für die Unschärferelation

Hier sind einige konkrete Beispiele, die die Auswirkungen der Unschärferelation veranschaulichen:

Elektronenmikroskopie: Um winzige Objekte wie Viren zu beobachten, nutzen Elektronenmikroskope Elektronenstrahlen. Die hohe Auflösung erfordert jedoch eine präzise Ortsbestimmung der Elektronen, was wiederum ihre Impulse beeinflusst und zu einer gewissen Unschärfe im Bild führt.
Laserkühlung: In der Quantenoptik werden Atome mithilfe von Lasern auf extrem niedrige Temperaturen abgekühlt. Die Unschärferelation begrenzt jedoch die Genauigkeit der Kühlung, da eine immer präzisere Ortsbestimmung der Atome zu einer zunehmenden Unschärfe ihres Impulses und damit ihrer kinetischen Energie führt.

Häufige Fragen zur Unschärferelation

Hier sind einige häufig gestellte Fragen und Antworten zur Unschärferelation:

Gilt die Unschärferelation nur für kleine Teilchen?
Nein, die Unschärferelation gilt für alle Objekte, aber sie ist nur auf der Quantenebene wirklich relevant, da die Unschärfe bei makroskopischen Objekten vernachlässigbar klein ist.
Widerspricht die Unschärferelation dem Determinismus?
Ja, die Unschärferelation impliziert, dass es eine fundamentale Grenze für die Vorhersagbarkeit in der Quantenwelt gibt. Wir können den Ausgang von Quantenereignissen nur mit einer bestimmten Wahrscheinlichkeit vorhersagen.

Fazit

Heisenbergs Unschärferelation ist ein Eckpfeiler der Quantenmechanik, der unser Verständnis der Welt auf fundamentaler Ebene verändert hat. Sie zeigt uns, dass es in der Quantenwelt keine absolute Gewissheit gibt, sondern dass Wahrscheinlichkeit und Unschärfe integrale Bestandteile der Realität sind. Obwohl sie auf den ersten Blick paradox erscheinen mag, eröffnet die Unschärferelation neue Perspektiven und Möglichkeiten, von der Stabilität der Materie bis hin zu revolutionären Technologien wie dem Quantencomputer.