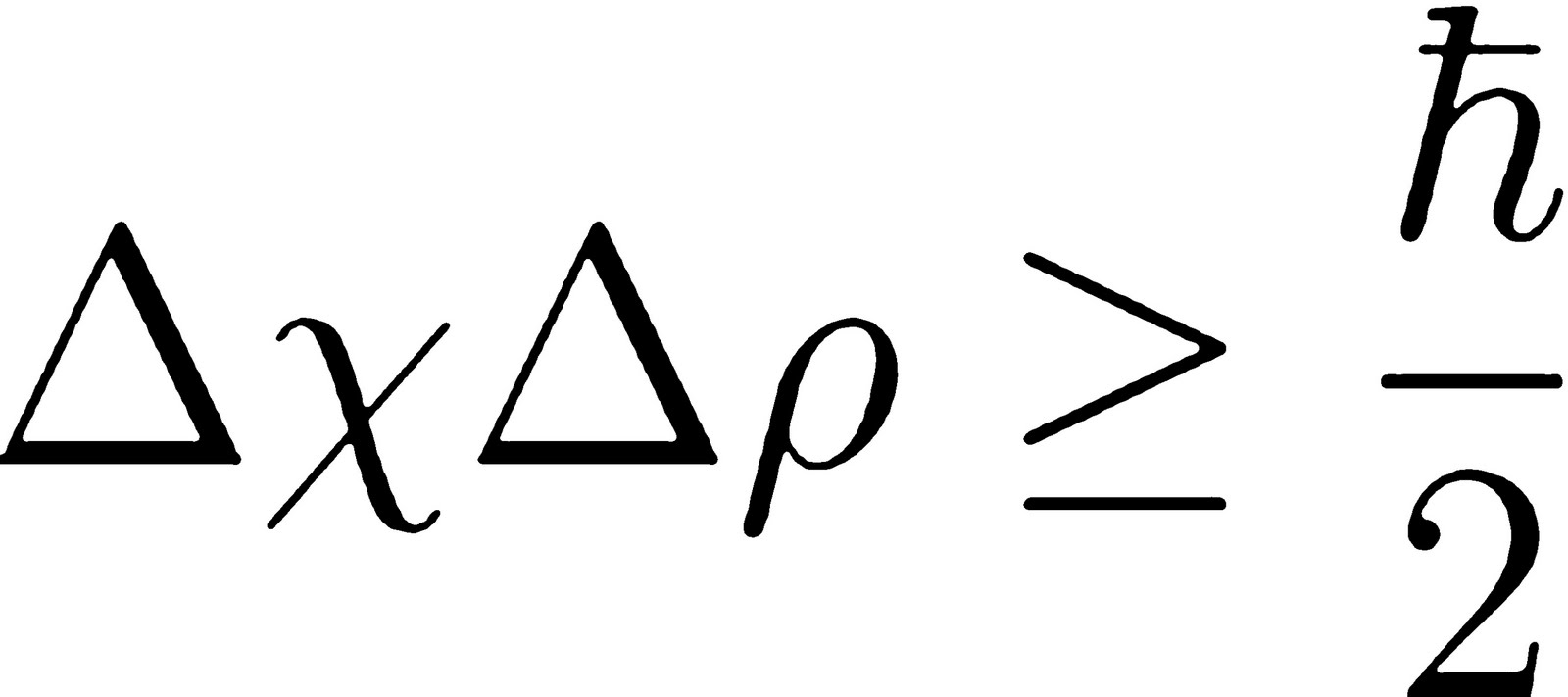Heisenbergs Unschärferelation Herleitung: Ein Einblick in die Quantenwelt

20 Mar 2024
de
Emil

heisenberg's uncertainty principle derivation

Stellen Sie sich vor, Sie versuchen, den genauen Standort und die Geschwindigkeit eines winzigen Elektrons gleichzeitig zu bestimmen. In der Welt der klassischen Physik wäre das ein Kinderspiel. Doch in der Quantenwelt stoßen wir auf eine fundamentale Grenze, die unsere Vorstellungskraft herausfordert: die Heisenberg'sche Unschärferelation.

Diese Relation, die 1927 vom deutschen Physiker Werner Heisenberg aufgestellt wurde, besagt, dass es unmöglich ist, sowohl den Ort als auch den Impuls (und damit die Geschwindigkeit) eines Teilchens gleichzeitig mit absoluter Präzision zu messen. Je genauer wir den Ort eines Teilchens bestimmen, desto ungenauer wird unsere Kenntnis seines Impulses – und umgekehrt.

Die Unschärferelation lässt sich mathematisch durch eine Ungleichung ausdrücken, die besagt, dass das Produkt der Unschärfen von Ort (Δx) und Impuls (Δp) eines Teilchens immer größer oder gleich dem reduzierten Planck'schen Wirkungsquantum (ħ) geteilt durch 2 ist: Δx * Δp ≥ ħ/2. Diese Gleichung zeigt, dass die Unschärfen nicht beliebig klein werden können.

Die Herleitung der Heisenberg'schen Unschärferelation basiert auf der Wellennatur von Teilchen, wie sie in der Quantenmechanik beschrieben wird. Demnach können Teilchen nicht nur als klassische Teilchen, sondern auch als Wellen betrachtet werden. Die Wellenfunktion eines Teilchens beschreibt die Wahrscheinlichkeit, das Teilchen an einem bestimmten Ort zu finden. Je genauer wir den Ort eines Teilchens bestimmen wollen, desto stärker müssen wir die Wellenfunktion "lokalisieren". Dies führt jedoch zu einer größeren Unschärfe im Impulsraum, da eine stark lokalisierte Welle aus einer Überlagerung vieler verschiedener Wellen mit unterschiedlichen Impulsen besteht.

Die Heisenberg'sche Unschärferelation hat tiefgreifende Auswirkungen auf unser Verständnis der Natur. Sie bedeutet, dass es eine grundlegende Grenze für unsere Fähigkeit gibt, Vorhersagen über das Verhalten von Quantensystemen zu treffen. Selbst wenn wir alle Informationen über den aktuellen Zustand eines Systems haben, können wir seinen zukünftigen Zustand nicht mit absoluter Sicherheit vorhersagen. Diese Unschärfe ist keine Folge von Unzulänglichkeiten unserer Messgeräte, sondern eine inhärente Eigenschaft der Quantenwelt.

Vorteile der Heisenberg'schen Unschärferelation

Obwohl die Heisenberg'sche Unschärferelation oft als eine Beschränkung unserer Möglichkeiten betrachtet wird, hat sie auch einige positive Seiten:

Stabilität der Materie: Die Unschärferelation verhindert, dass Elektronen in ein Atom kollabieren. Würde der Impuls eines Elektrons beliebig klein, wäre sein Aufenthaltsort so unscharf, dass es sich mit dem Kern überlappen und von diesem eingefangen werden würde. Die Unschärferelation sorgt dafür, dass die Elektronen in einem stabilen Abstand zum Kern verbleiben.
Tunneleffekt: Die Unschärferelation ermöglicht es Teilchen, Energiebarrieren zu überwinden, die sie klassisch nicht überwinden könnten. Dies ist möglich, da die Energie eines Teilchens für kurze Zeit unscharf sein kann. Der Tunneleffekt spielt eine wichtige Rolle bei vielen physikalischen Prozessen, wie z.B. beim radioaktiven Zerfall und bei der Funktionsweise von Transistoren.
Quantencomputer: Die Heisenberg'sche Unschärferelation ist eine der Grundlagen für die Entwicklung von Quantencomputern. Diese neuartigen Computer nutzen die Prinzipien der Quantenmechanik, um bestimmte Aufgaben viel schneller zu lösen als klassische Computer.

Häufige Fragen zur Heisenberg'schen Unschärferelation

Was genau besagt die Heisenberg'sche Unschärferelation?

Die Heisenberg'sche Unschärferelation besagt, dass bestimmte Paare von physikalischen Größen, wie Ort und Impuls oder Energie und Zeit, nicht gleichzeitig mit beliebiger Genauigkeit gemessen werden können.

Gilt die Unschärferelation nur für kleine Teilchen?

Nein, die Unschärferelation gilt für alle Objekte, unabhängig von ihrer Größe. Allerdings ist der Effekt bei makroskopischen Objekten so klein, dass er in der Praxis keine Rolle spielt.

Widerspricht die Unschärferelation dem Determinismus?

Ja, die Heisenberg'sche Unschärferelation stellt den klassischen Determinismus in Frage, der davon ausgeht, dass der zukünftige Zustand eines Systems eindeutig durch seinen gegenwärtigen Zustand bestimmt ist.

Ist die Unschärferelation nur eine theoretische Vorhersage?

Nein, die Heisenberg'sche Unschärferelation wurde in unzähligen Experimenten bestätigt und ist eine der am besten überprüften Theorien der Physik.

Was sind die philosophischen Implikationen der Unschärferelation? Die Heisenberg'sche Unschärferelation wirft Fragen nach der Natur der Realität, der Objektivität von Messungen und den Grenzen der menschlichen Erkenntnis auf.

Fazit

Die Heisenberg'sche Unschärferelation ist ein Eckpfeiler der Quantenmechanik und hat unser Verständnis der Welt auf fundamentaler Ebene revolutioniert. Sie zeigt uns, dass die Quantenwelt ihren eigenen Gesetzen gehorcht, die unserer Intuition oft widersprechen. Obwohl die Unschärferelation oft als eine Begrenzung unserer Möglichkeiten betrachtet wird, eröffnet sie uns auch neue Perspektiven und ermöglicht technologische Fortschritte wie die Entwicklung von Quantencomputern. Das Studium der Heisenberg'schen Unschärferelation ist daher unerlässlich für alle, die die faszinierende Welt der Quantenmechanik verstehen wollen.