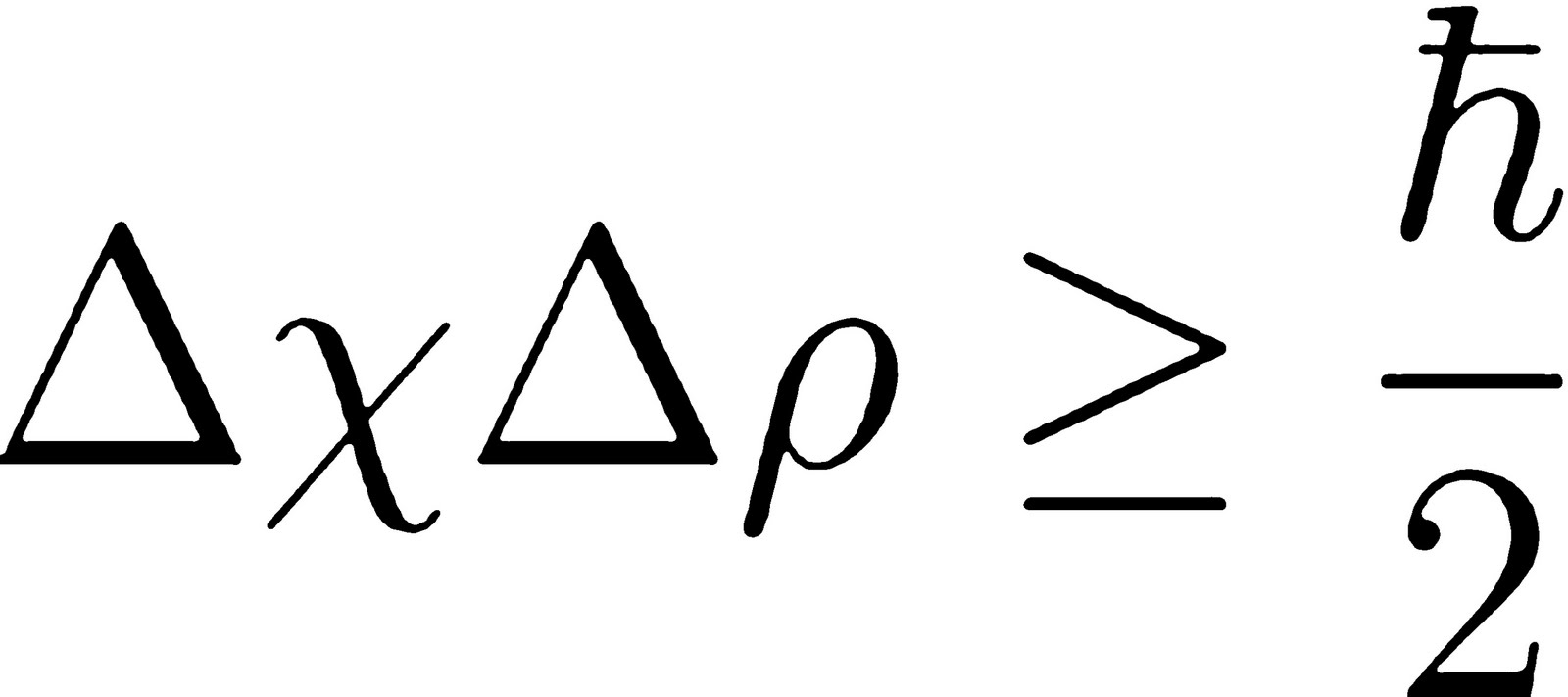Stell dir vor, du könntest gleichzeitig genau wissen, wo etwas ist und wie schnell es sich bewegt. Klingt erstmal logisch, oder? In der Welt der Quantenphysik ist das aber nicht ganz so einfach. Hier kommt die Heisenbergsche Unschärferelation ins Spiel, eines der fundamentalen Prinzipien der Quantenmechanik, das unsere Vorstellungskraft auf die Probe stellt.
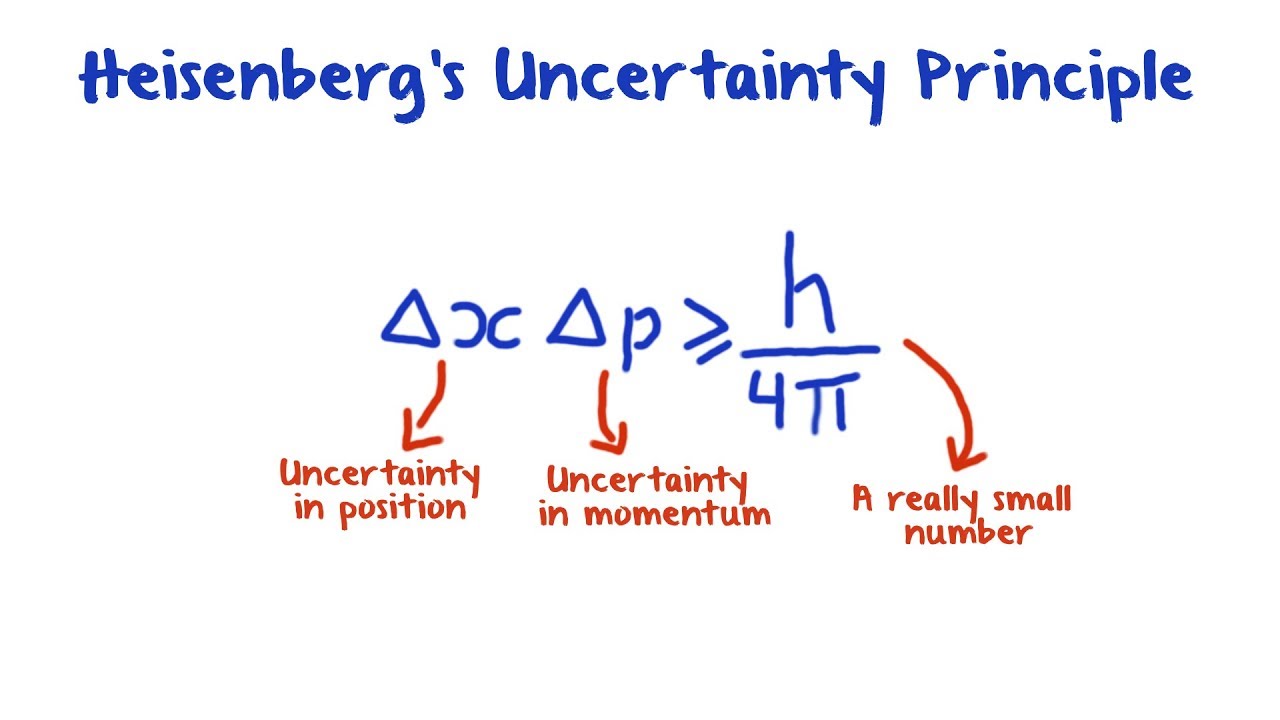
Formuliert wurde diese revolutionäre Idee erstmals 1927 vom deutschen Physiker Werner Heisenberg. Heisenberg's uncertainty principle states, dass man nicht gleichzeitig den Ort und den Impuls eines Teilchens beliebig genau bestimmen kann. Das klingt vielleicht erstmal abstrakt, hat aber enorme Auswirkungen auf unser Verständnis der Welt im Kleinsten.
Was bedeutet das jetzt genau? Der Impuls eines Teilchens beschreibt seine Bewegung, also wie schnell es sich in welche Richtung bewegt. Heisenbergs Unschärferelation besagt nun, dass je genauer wir den Ort eines Teilchens messen, desto ungenauer wird unsere Messung seines Impulses – und umgekehrt. Das liegt nicht an unseren Messinstrumenten, sondern ist ein fundamentales Prinzip der Natur!
Man kann sich das so vorstellen: Um den Ort eines Elektrons zu bestimmen, könnten wir es mit Licht "beleuchten". Je kürzer die Wellenlänge des Lichts, desto genauer können wir den Ort des Elektrons bestimmen. Kurzwelliges Licht hat aber auch eine höhere Energie und beeinflusst damit den Impuls des Elektrons stärker. Je genauer wir also den Ort messen wollen, desto stärker verändern wir den Impuls – und umgekehrt.
Die Heisenbergsche Unschärferelation hat weitreichende Konsequenzen für unser Verständnis der Welt. Sie zeigt, dass es in der Quantenwelt prinzipielle Grenzen für unsere Messungen gibt und dass wir die Natur nicht beliebig genau erfassen können. Das hat auch Auswirkungen auf unser Bild von Kausalität und Determinismus, denn wenn wir Ort und Impuls nicht gleichzeitig kennen können, können wir auch die zukünftige Bewegung eines Teilchens nicht exakt vorhersagen.
Vorteile der Heisenbergschen Unschärferelation
Die Heisenbergsche Unschärferelation mag auf den ersten Blick einschränkend wirken, doch sie ist auch die Grundlage für viele Phänomene und Technologien:
- Existenz von Atomen: Die Unschärferelation verhindert, dass Elektronen in den Atomkern stürzen. Würden wir Ort und Impuls gleichzeitig genau kennen, würden die Elektronen ihre Energie verlieren und in den Kern fallen. Die Unschärfe sorgt dafür, dass sie in einem bestimmten Abstand zum Kern verbleiben.
- Tunneleffekt: Die Unschärferelation erlaubt es Teilchen, Energiebarrieren zu "durchtunneln", die sie klassisch nicht überwinden könnten. Das ist die Grundlage für viele Phänomene, z.B. in der Kernfusion oder in Transistoren.
- Quantencomputer: Die Prinzipien der Quantenmechanik, einschließlich der Unschärferelation, ermöglichen die Entwicklung von Quantencomputern, die bestimmte Aufgaben viel schneller lösen könnten als klassische Computer.
Beispiele für die Heisenbergsche Unschärferelation
Die Unschärferelation zeigt sich in vielen Bereichen der Quantenphysik, z.B.:
- Beugung von Elektronen an einem Spalt: Lässt man Elektronen durch einen schmalen Spalt fliegen, weitet sich der Elektronenstrahl hinter dem Spalt auf. Das liegt daran, dass die Position der Elektronen am Spalt sehr genau definiert ist, wodurch ihr Impuls unscharf wird und sie sich in verschiedene Richtungen bewegen.
- Nullpunktsenergie: Die Unschärferelation verhindert, dass ein quantenmechanischer harmonischer Oszillator jemals vollständig zur Ruhe kommt. Es bleibt immer eine Restenergie, die Nullpunktsenergie.
Häufige Fragen zur Heisenbergschen Unschärferelation
Die Heisenbergsche Unschärferelation ist ein komplexes Thema, das oft zu Fragen führt. Hier sind einige der häufigsten:
- Gilt die Unschärferelation nur für Quantenobjekte? Ja, die Unschärferelation spielt nur in der Quantenwelt eine Rolle. Für makroskopische Objekte ist die Unschärfe so gering, dass sie vernachlässigt werden kann.
- Bedeutet die Unschärferelation, dass die Welt zufällig ist? Die Unschärferelation bedeutet nicht, dass die Welt zufällig ist, sondern dass wir bestimmte Größenpaare nicht gleichzeitig beliebig genau kennen können. Die Quantenmechanik ist zwar probabilistisch, aber nicht völlig unvorhersagbar.
Die Heisenbergsche Unschärferelation ist ein fundamentaler Bestandteil der Quantenmechanik und revolutionierte unser Verständnis der Welt im Kleinsten. Sie zeigt, dass es prinzipielle Grenzen für unsere Messungen gibt und dass die Natur nicht beliebig genau erfassbar ist. Gleichzeitig ist die Unschärferelation Grundlage für viele Phänomene und Technologien, die unser Leben beeinflussen. Die Erforschung der Quantenwelt und ihrer Gesetze ist noch lange nicht abgeschlossen und verspricht weiterhin spannende Erkenntnisse über die Natur unseres Universums.
heisenberg's uncertainty principle states - Trees By Bike
heisenberg's uncertainty principle states - Trees By Bike
heisenberg's uncertainty principle states - Trees By Bike
Heisenberg Uncertainty Principle Of Finance - Trees By Bike
heisenberg's uncertainty principle states - Trees By Bike
Certainly Uncertain: What's Heisenberg's Uncertainty Principle - Trees By Bike
heisenberg's uncertainty principle states - Trees By Bike
Heisenberg's Uncertainty Principle And Borns Equation Presentation - Trees By Bike
heisenberg's uncertainty principle states - Trees By Bike
Explain the Heisenberg Uncertainty Principle, and how the - Trees By Bike
Probability: The Heisenberg Uncertainty Principle - Trees By Bike
Heisenberg Uncertainty Principle Formula Sheet - Trees By Bike
Heisenberg's Uncertainty Principle And Borns Equation Presentation - Trees By Bike
Heisenberg Uncertainty Principle Definition, Equation, and Application - Trees By Bike
Quantum for Dummies (part 16). Essentials: Heisenberg - Trees By Bike