Was macht ein Quadrat eigentlich aus? Seine vier gleichen Seiten, klar. Aber was ist mit der Höhe? Ist das nicht dasselbe wie die Seitenlänge? Genau darum geht es hier! Tauchen wir ein in die faszinierende Welt des Quadrats und seiner Seitenlänge – dem Schlüssel zu seinem Wesen.
Die sogenannte "altura de un cuadrado", also die Höhe eines Quadrats, ist nichts anderes als die Länge einer seiner Seiten. Klingt einfach? Ist es auch! Doch diese simple Erkenntnis ist grundlegend für das Verständnis der Geometrie und hat weitreichende Anwendungen, von der Architektur bis zur Kunst.
Stellen Sie sich vor, Sie möchten ein quadratisches Beet anlegen. Ohne die Kenntnis der Seitenlänge, also der Höhe, wären Sie völlig verloren. Wie viel Erde brauchen Sie? Wie lang müssen die Holzbretter sein, die Sie als Umrandung verwenden möchten? Die Seitenlänge ist der Schlüssel!
Die Geschichte der Geometrie, und damit auch des Quadrats, reicht Jahrtausende zurück. Schon die alten Ägypter nutzten die Eigenschaften des Quadrats für die Landvermessung und den Bau von Pyramiden. Die "altura de un cuadrado" war für sie ein essentielles Werkzeug.
Die Bedeutung der Seitenlänge eines Quadrats liegt in ihrer direkten Verbindung zu allen anderen Eigenschaften des Quadrats. Flächeninhalt, Umfang, Diagonalen – all diese Größen lassen sich direkt aus der Seitenlänge berechnen. Sie ist der Dreh- und Angelpunkt des Quadrats.
Die Seitenlänge eines Quadrats ist definiert als die Distanz zwischen zwei benachbarten Eckpunkten. Ein Quadrat mit einer Seitenlänge von 5 cm hat also eine Höhe von 5 cm. Genauso einfach ist das.
Vorteile der Kenntnis der Seitenlänge eines Quadrats sind vielfältig. Erstens: Einfache Berechnung des Flächeninhalts. Seitenlänge mal Seitenlänge – fertig! Zweitens: Leichte Bestimmung des Umfangs. Vier mal die Seitenlänge – kinderleicht! Drittens: Schnelle Berechnung der Diagonalen. Seitenlänge mal Wurzel aus zwei – und schon haben wir das Ergebnis.
Angenommen, Sie möchten ein quadratisches Bild mit einer Seitenlänge von 20 cm rahmen. Sie benötigen also vier Leisten von jeweils 20 cm Länge. Der Flächeninhalt des Bildes beträgt 20 cm x 20 cm = 400 cm². So einfach ist das mit der Kenntnis der Seitenlänge.
Häufig gestellte Fragen:
1. Was ist die altura de un cuadrado? - Die Seitenlänge.
2. Wie berechnet man den Flächeninhalt eines Quadrats? - Seitenlänge mal Seitenlänge.
3. Wie berechnet man den Umfang eines Quadrats? - Vier mal die Seitenlänge.
4. Wie berechnet man die Diagonale eines Quadrats? - Seitenlänge mal Wurzel aus zwei.
5. Ist die Höhe eines Quadrats gleich seiner Seitenlänge? - Ja.
6. Welche Bedeutung hat die Seitenlänge eines Quadrats? - Sie ist die Grundlage für die Berechnung aller anderen Eigenschaften.
7. Wo findet die Seitenlänge eines Quadrats Anwendung? - In der Geometrie, Architektur, Kunst, etc.
8. Was ist der Unterschied zwischen Seitenlänge und Höhe eines Quadrats? - Es gibt keinen Unterschied.
Tipps und Tricks: Merken Sie sich einfach: Seitenlänge gleich Höhe! Das vereinfacht vieles.
Zusammenfassend lässt sich sagen, dass die "altura de un cuadrado", also die Seitenlänge, das Herzstück des Quadrats ist. Sie ist die Grundlage für die Berechnung aller wichtigen Eigenschaften und somit unverzichtbar für das Verständnis dieser geometrischen Figur. Von der Berechnung des Flächeninhalts eines Beetes bis zur Konstruktion komplexer architektonischer Strukturen – die Seitenlänge des Quadrats spielt eine zentrale Rolle. Vertiefen Sie Ihr Wissen über das Quadrat und seine Seitenlänge, und Sie werden die Welt der Geometrie mit neuen Augen sehen. Erkunden Sie die faszinierende Welt der Quadrate und entdecken Sie die unzähligen Möglichkeiten, die sich Ihnen durch das Verständnis der Seitenlänge eröffnen!
altura de un cuadrado - Trees By Bike
A partir de un cartón cuadrado un grupo de estudiantes piensa - Trees By Bike
altura de un cuadrado - Trees By Bike
cueva Referéndum clásico area del triangulo y perimetro sección masa - Trees By Bike
Ejercicios resueltos Perímetro y área - Trees By Bike
altura de un cuadrado - Trees By Bike
Determina el área de un cuadrado cuya fórmula es L x L En pasos por - Trees By Bike
como sacar el área del cuadrado de primaria - Trees By Bike
3 Ways to Find the Area of a Square - Trees By Bike
Cómo calcular metros cuadrados en arquitectura - Trees By Bike
Formula Para Calcular El Perimetro Y Area Del Cuadrado - Trees By Bike
frutas Despertar Paralizar cuanto mide el lado de un cuadrado cuya - Trees By Bike
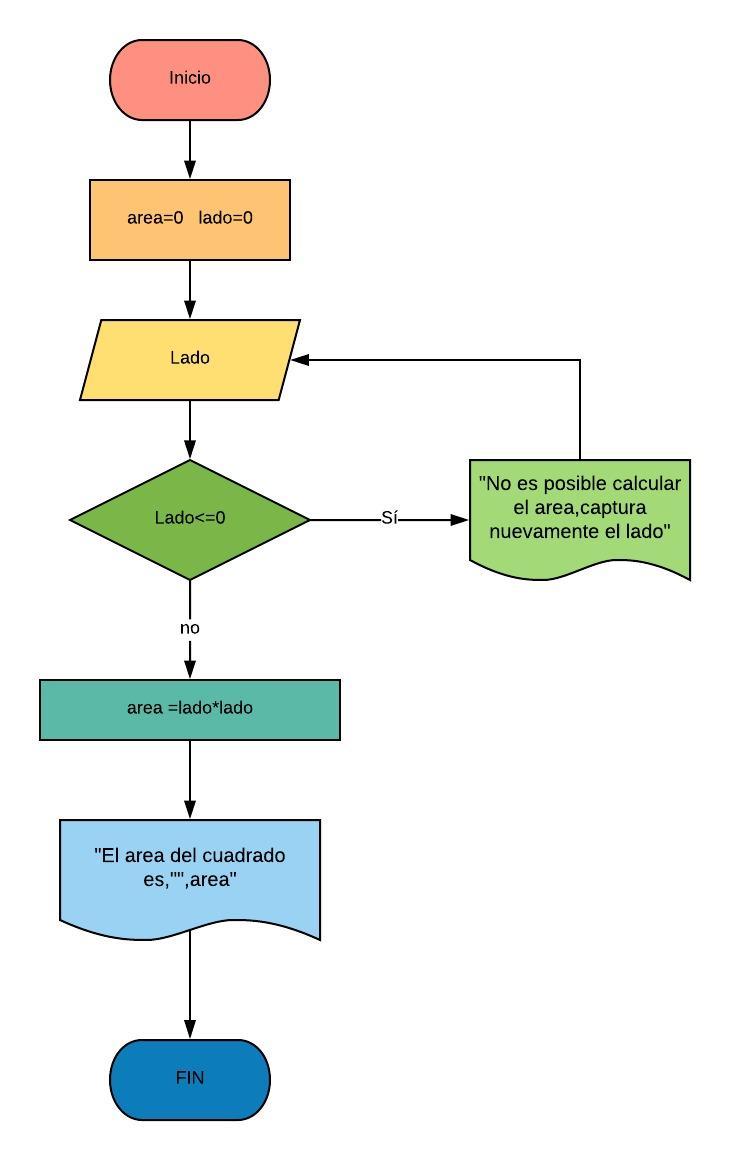
Diagrama De Flujo Para Calcular El Area De Un Cuadrado - Trees By Bike
Como Se Calcula El Area De Un Cuadrado - Trees By Bike
Ejercicios Resueltos Del Teorema De La Altura Y Razones - Trees By Bike