Stell dir vor, du könntest zwei verschiedene Dinge kombinieren und etwas völlig Neues erschaffen. In der Mathematik, genauer gesagt in der Algebra, machen wir das ständig mit Funktionen! Hier kommt die "Summe von zwei Funktionen" ins Spiel. Aber was genau bedeutet das, und wozu ist es gut?
Im Grunde ist es ganz einfach: Stell dir zwei Funktionen vor, sagen wir f(x) und g(x). Die Summe dieser beiden Funktionen, geschrieben als (f + g)(x), bedeutet nichts anderes, als dass wir für jeden x-Wert die Funktionswerte von f(x) und g(x) addieren. Klingt erstmal unspektakulär, eröffnet aber eine Welt voller Möglichkeiten, komplexe Zusammenhänge zu modellieren und zu analysieren.
Die Geschichte der Funktionen reicht weit zurück, bis ins antike Griechenland. Schon damals erkannten Mathematiker die Notwendigkeit, Zusammenhänge zwischen verschiedenen Größen zu beschreiben. Die Idee der Summe von Funktionen entstand jedoch erst viel später, im Zuge der Entwicklung der Algebra. Heute ist dieses Konzept aus der Mathematik nicht mehr wegzudenken und findet Anwendung in verschiedensten Bereichen, von der Physik bis hin zur Informatik.
Ein einfaches Beispiel verdeutlicht das Prinzip: Nehmen wir an, f(x) = 2x und g(x) = x². Die Summe (f + g)(x) wäre dann 2x + x². Für x = 2 wäre der Funktionswert (f + g)(2) = 2*2 + 2² = 8.
Aber wozu das Ganze? Nun, die Summe von Funktionen hilft uns, komplexe Phänomene zu zerlegen und zu verstehen. Sie ist essenziell für die Modellierung realer Prozesse, die von mehreren Faktoren abhängen. Von der Berechnung von Flugbahnen bis hin zur Analyse von Finanzmärkten – die Summe von Funktionen ist überall mit dabei!
Vorteile der Summe von zwei Funktionen
Die Anwendung der Summe von zwei Funktionen bietet diverse Vorteile:
- Vereinfachung komplexer Probleme: Durch das Aufteilen in Teilfunktionen wird die Analyse und Lösung erleichtert.
- Flexibilität: Unterschiedliche Funktionen können kombiniert werden, um spezifische Anforderungen zu erfüllen.
- Verbesserte Modellierung: Reale Phänomene können durch die Kombination verschiedener Einflussfaktoren genauer abgebildet werden.
Nachteile der Summe von zwei Funktionen
Trotz der zahlreichen Vorteile gibt es auch einige potenzielle Nachteile:
- Komplexität: In einigen Fällen kann die Kombination von Funktionen zu komplexeren Gleichungen und Berechnungen führen.
- Interpretation: Die Interpretation der Ergebnisse kann schwieriger sein, insbesondere bei komplexeren Kombinationen von Funktionen.
Tipps und Tricks zur Arbeit mit der Summe von Funktionen
- Verwende grafische Darstellungen: Visualisiere die Funktionen und ihre Summe, um ein besseres Verständnis zu erlangen.
- Nutze mathematische Software: Programme wie Wolfram Alpha oder GeoGebra können bei der Berechnung und Visualisierung helfen.
- Übung macht den Meister: Je mehr du mit Funktionen arbeitest, desto vertrauter wirst du mit der Materie.
Die Summe von zwei Funktionen ist ein mächtiges Werkzeug in der Mathematik und findet breite Anwendung in verschiedenen Disziplinen. Sie ermöglicht es uns, komplexe Zusammenhänge zu modellieren, zu analysieren und zu verstehen. Von der Physik bis hin zur Finanzwelt – die Summe von Funktionen hilft uns, die Welt um uns herum besser zu begreifen und zu gestalten. Also, keine Angst vor der Mathematik – sie ist der Schlüssel zu einer Welt voller faszinierender Entdeckungen!
SUMMEWENNS einfach erklärt - Trees By Bike
summe von zwei funktionen - Trees By Bike
summe von zwei funktionen - Trees By Bike
Die Excel WENN DANN Funktion / Formel ganz einfach erklärt - Trees By Bike
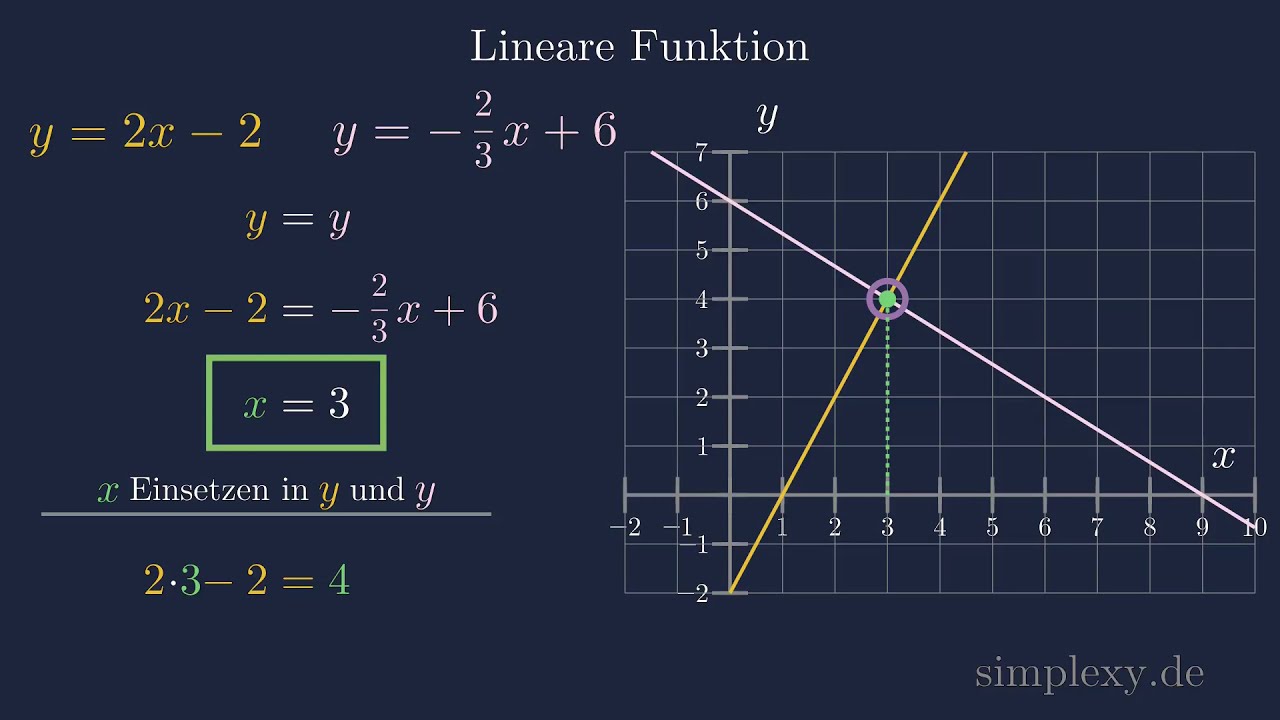
Schnittpunkte Zweier Geraden Berechnen - Trees By Bike
summe von zwei funktionen - Trees By Bike
summe von zwei funktionen - Trees By Bike
Die Excel SUMMEWENN Funktion ganz einfach erklärt - Trees By Bike
summe von zwei funktionen - Trees By Bike
Regeln zum Lösen von Exponentialgleichungen - Trees By Bike
Textaufgaben Klasse 4 (Schwerpunkt schriftliche Division) mit Lösungen - Trees By Bike
summe von zwei funktionen - Trees By Bike
summe von zwei funktionen - Trees By Bike
summe von zwei funktionen - Trees By Bike
Ableitungsregeln: Differenzieren einer Summe von Funktionen - Trees By Bike