Imagina un mundo sin ruedas, sin latas de conserva, sin tuberías... ¡Parece imposible, ¿verdad?! Estos objetos tan cotidianos comparten una forma geométrica fundamental: el cilindro. Comprender el área y el volumen de un cilindro no solo es esencial para las matemáticas, sino que también abre las puertas para entender el diseño y la funcionalidad de innumerables objetos a nuestro alrededor.
El área de un cilindro se refiere a la medida de su superficie, es decir, cuánto espacio ocupa en dos dimensiones. Por otro lado, el volumen del cilindro nos indica la cantidad de espacio tridimensional que ocupa, es decir, cuánto puede contener.
Desde la antigüedad, el ser humano ha utilizado el cilindro en la construcción, la ingeniería y la vida cotidiana. Los antiguos egipcios, por ejemplo, empleaban cilindros de piedra para mover grandes bloques durante la construcción de las pirámides. En la actualidad, los cilindros son omnipresentes, desde los motores de los coches hasta los envases de alimentos.
Calcular el área y el volumen de un cilindro no es solo un ejercicio académico. Estos cálculos tienen aplicaciones prácticas en campos como la arquitectura, la ingeniería mecánica, la construcción e incluso la cocina. Por ejemplo, para diseñar un tanque de almacenamiento de agua, es crucial conocer su volumen para determinar su capacidad.
Uno de los principales desafíos al trabajar con el área y el volumen de un cilindro es la correcta aplicación de las fórmulas y la comprensión de las unidades de medida. Es fácil confundirse entre el área, que se mide en unidades cuadradas (como cm²), y el volumen, que se mide en unidades cúbicas (como cm³).
Para calcular el área total de un cilindro, se utiliza la siguiente fórmula:
Área Total = 2πr(r + h)
Donde:
π (pi) ≈ 3.1416
r = radio del cilindro
h = altura del cilindro
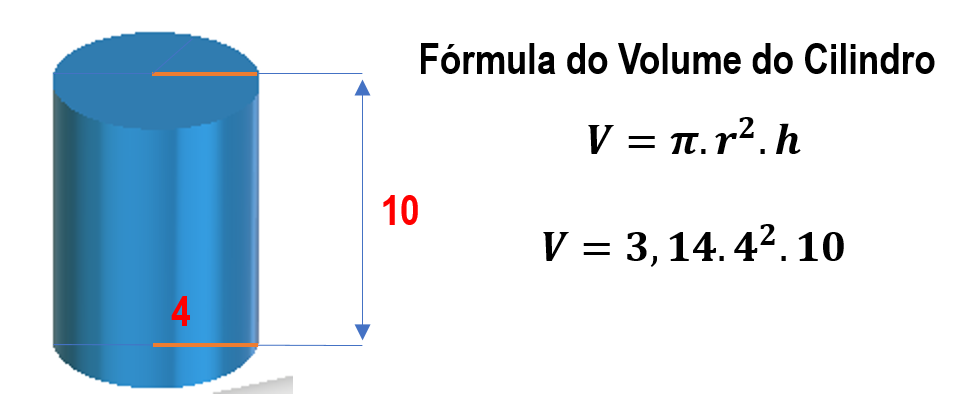
Para calcular el volumen de un cilindro, se utiliza la siguiente fórmula:
Volumen = πr²h
Donde:
π (pi) ≈ 3.1416
r = radio del cilindro
h = altura del cilindro
Veamos un ejemplo sencillo. Imaginemos un cilindro con un radio de 5 cm y una altura de 10 cm. Para calcular su área total, aplicamos la fórmula:
Área Total = 2π(5 cm)(5 cm + 10 cm) = 2π(5 cm)(15 cm) ≈ 471.24 cm²
Para calcular su volumen, usamos la fórmula correspondiente:
Volumen = π(5 cm)²(10 cm) ≈ 785.4 cm³
Ventajas y Desventajas del Uso de Cilindros
| Ventajas | Desventajas |
|---|---|
| Fáciles de fabricar | Pueden rodar fácilmente |
| Apilables y fáciles de almacenar | No son la forma más eficiente en términos de espacio |
| Resistentes a la presión | Dificultad para acceder a las esquinas |
Comprender el área y el volumen de los cilindros es fundamental en diversas áreas. Dominar estos conceptos nos permite no solo resolver problemas matemáticos, sino también comprender mejor el mundo que nos rodea.
area e volume do cilindro - Trees By Bike
Área e volume do cilindro - Trees By Bike
Pin em Matérias - Trees By Bike
Formula Calculo De Volume Cilindro - Trees By Bike
area e volume do cilindro - Trees By Bike
Sem teto Hornet Ficar bravo calculo de volume de cilindro gancho Ervas - Trees By Bike
Como Calcular Area Del Cilindro - Trees By Bike
Realizar cálculos práticos com volume e capacidade do cilindro reto - Trees By Bike
Volume do cilindro: definição, cálculos e figuras geométricas - Trees By Bike
Prismas e Cilindros no Enem - Trees By Bike
Calcular Area Do Cilindro - Trees By Bike
Area E Volume Do Cilindro Exemplos - Trees By Bike
Calcular Area Lateral De Um Cilindro - Trees By Bike
Cilindro: Área, Volume e Classificação - Trees By Bike
Volume do Cilindro: Fórmula e Exercício Resolvido - Trees By Bike