Imaginez un instant un graphique boursier affichant l'évolution du prix d'une action. Comment déterminer avec précision le taux de variation du cours à un instant précis ? C'est là que la notion de tangente à une courbe entre en jeu. Loin d'être un concept réservé aux mathématiques pures, le tracé de la tangente à une courbe possède des applications concrètes dans de nombreux domaines, allant de l'économie à la physique en passant par l'ingénierie.
Mais qu'est-ce qu'une tangente exactement ? En termes simples, la tangente à une courbe en un point donné est une droite qui "frôle" la courbe en ce point, épousant sa direction instantanée. Imaginez une voiture roulant sur une route sinueuse. À chaque instant, la direction de la voiture est représentée par la tangente à la trajectoire de la voiture en ce point.
L'histoire du tracé de la tangente remonte à l'Antiquité, avec des contributions notables de mathématiciens grecs comme Euclide et Archimède. Cependant, c'est avec le développement du calcul infinitésimal au XVIIe siècle, notamment grâce aux travaux de Pierre de Fermat et d'Isaac Newton, que la notion de tangente a pris toute son importance. Le calcul infinitésimal a permis de formaliser la notion de "frollement" et de développer des méthodes rigoureuses pour calculer l'équation de la tangente.
L'importance du tracé de la tangente réside dans sa capacité à nous fournir des informations précieuses sur le comportement local d'une courbe. En effet, la pente de la tangente en un point donné représente le taux de variation instantané de la courbe en ce point. Cette information est cruciale dans de nombreux domaines pour comprendre et modéliser des phénomènes dynamiques.
Prenons l'exemple de la physique. La vitesse d'un objet en mouvement est définie comme le taux de variation de sa position en fonction du temps. Graphiquement, la vitesse à un instant donné est représentée par la pente de la tangente à la courbe représentant la position de l'objet en fonction du temps. De même, l'accélération, qui représente la variation de la vitesse en fonction du temps, est donnée par la pente de la tangente à la courbe de la vitesse.
En économie, la tangente est utilisée pour analyser les fonctions de coût, de revenu et de profit. La pente de la tangente à la courbe de coût total en un point donné représente le coût marginal, c'est-à-dire le coût supplémentaire engendré par la production d'une unité supplémentaire. Cette information est essentielle pour les entreprises qui cherchent à optimiser leur production et à maximiser leurs profits.
Le tracé de la tangente à une courbe est un outil puissant pour comprendre et analyser le comportement des fonctions mathématiques. Son importance transcende les frontières des mathématiques pures pour trouver des applications dans de nombreux domaines scientifiques et techniques. Que ce soit pour modéliser la trajectoire d'un objet en mouvement, analyser les performances économiques d'une entreprise ou encore prédire l'évolution d'une population, la tangente se révèle être un outil précieux pour décrypter le monde qui nous entoure.
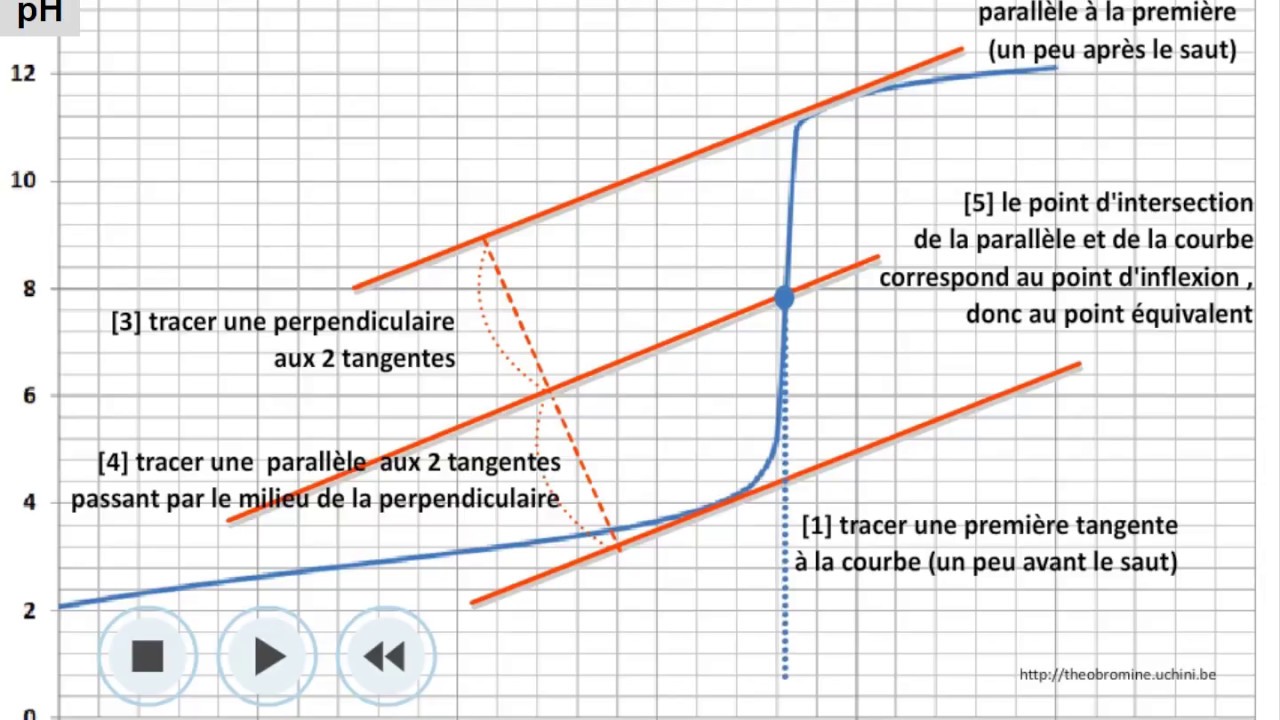
tracer la tangente d'une courbe - Trees By Bike
tracer la tangente d'une courbe - Trees By Bike
tracer la tangente d'une courbe - Trees By Bike
tracer la tangente d'une courbe - Trees By Bike
tracer la tangente d'une courbe - Trees By Bike
tracer la tangente d'une courbe - Trees By Bike
tracer la tangente d'une courbe - Trees By Bike
tracer la tangente d'une courbe - Trees By Bike
tracer la tangente d'une courbe - Trees By Bike
tracer la tangente d'une courbe - Trees By Bike
tracer la tangente d'une courbe - Trees By Bike
tracer la tangente d'une courbe - Trees By Bike
tracer la tangente d'une courbe - Trees By Bike
tracer la tangente d'une courbe - Trees By Bike
tracer la tangente d'une courbe - Trees By Bike