Imaginez un chemin sinueux, une trajectoire élégante, une ligne qui danse sur une surface : c'est l'essence même d'une courbe. Mais que représente réellement ce concept, omniprésent dans notre monde, des montagnes aux gratte-ciel, des ondes sonores aux graphiques financiers ? Découvrons ensemble ce monde fascinant.
La nature d'une courbe est plus complexe qu'il n'y paraît. Il ne s'agit pas simplement d'une ligne non droite, mais d'un concept mathématique riche et varié. Une courbe peut être décrite comme un ensemble continu de points, formant une ligne qui change de direction sans angles brusques. Cette notion abstraite se manifeste concrètement dans d'innombrables formes, de la simple parabole au complexe tracé d'une spirale logarithmique.
L'histoire des courbes remonte à l'antiquité, avec des figures géométriques comme le cercle et l'ellipse étudiées par les Grecs. L'étude des courbes, un domaine central des mathématiques, a évolué au fil des siècles, des géomètres classiques aux mathématiciens modernes. Leur importance est indéniable, impactant des domaines aussi variés que la physique, l'ingénierie, l'architecture et même l'art.
Comprendre la nature d'une courbe est essentiel pour interpréter le monde qui nous entoure. Les courbes des graphiques, par exemple, nous permettent de visualiser et d'analyser des données complexes. En architecture, les courbes confèrent aux structures une esthétique unique et une résistance accrue. En physique, elles décrivent les trajectoires des objets en mouvement et les variations des ondes.
Définir une courbe avec précision peut s'avérer complexe, car il existe une multitude de types de courbes, chacune avec ses propres caractéristiques. Par exemple, une parabole est une courbe symétrique définie par une équation spécifique, tandis qu'une spirale s'enroule autour d'un point central. La compréhension de ces différentes formes et de leurs propriétés mathématiques est fondamentale dans de nombreuses disciplines.
Quelques exemples de courbes dans notre quotidien : la trajectoire d'une balle lancée en l'air, la forme d'un arc-en-ciel, le contour d'une feuille d'arbre. Ces exemples illustrent la diversité et l'ubiquité des courbes dans notre environnement.
L'étude des courbes permet de modéliser et de prédire des phénomènes naturels. Elle offre également des outils pour concevoir des structures plus efficaces et esthétiques. Enfin, la compréhension des courbes permet d'analyser des données complexes et d'en tirer des conclusions significatives.
Avantages et Inconvénients des Courbes
Pour approfondir la compréhension des courbes, explorons quelques questions fréquemment posées :
1. Qu'est-ce qu'une courbe plane ? Réponse : Une courbe qui se situe entièrement dans un plan.
2. Comment représenter mathématiquement une courbe ? Réponse : Par une équation ou une fonction.
3. Qu'est-ce que la courbure d'une courbe ? Réponse : Une mesure de combien une courbe s'éloigne d'une ligne droite.
4. Quels sont les différents types de courbes ? Réponse : Paraboles, hyperboles, ellipses, spirales, etc.
5. Comment les courbes sont-elles utilisées en physique ? Réponse : Pour décrire les trajectoires, les ondes, etc.
6. Comment les courbes sont-elles utilisées en architecture ? Réponse : Pour créer des formes esthétiques et résistantes.
7. Comment les courbes sont-elles utilisées en informatique graphique ? Réponse : Pour créer des images et des animations.
8. Qu'est-ce qu'une courbe de Bézier ? Réponse: Un type de courbe paramétrique utilisé en infographie.
En conclusion, les courbes, loin d'être de simples lignes ondulées, représentent un concept fondamental en mathématiques et dans de nombreuses disciplines appliquées. De la description des phénomènes naturels à la conception d'objets du quotidien, leur influence est omniprésente. Comprendre la nature et les propriétés des courbes ouvre la porte à une compréhension plus profonde du monde qui nous entoure. En explorant les différents types de courbes, leurs applications et leur importance, nous pouvons apprécier la richesse et la beauté de ce concept mathématique essentiel. Continuez à explorer le monde fascinant des courbes et découvrez les secrets qu'elles recèlent.
comment tracer une courbe dindifférence - Trees By Bike
les signaux sonores 4eme - Trees By Bike
c'est quoi une courbe - Trees By Bike
Découvrir 116 imagen extremum dune fonction formule - Trees By Bike
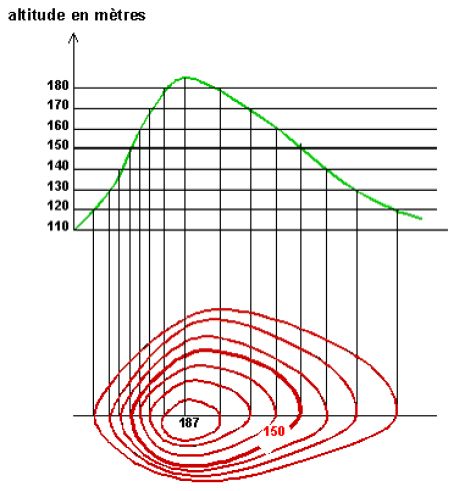
Les courbes de niveau - Trees By Bike
Ntroduire 98 imagen formule de la pente topographique - Trees By Bike
La fonction racine carrée Cours et exercices corrigés - Trees By Bike
Reconnaître la nature dun mouvement à partir dun graphique - Trees By Bike
Représenter des Données dans un Graphique Cartésien - Trees By Bike
Définir la dérivée dune fonction et linterpréter sur la tangente à - Trees By Bike
Les prix le principe de l - Trees By Bike
PDF motif elementaire PDF Télécharger Download - Trees By Bike
PDF lire et construire un graphique cm2 PDF Télécharger Download - Trees By Bike
Découvrir 112 imagen fonction affine formule - Trees By Bike
Cest quoi être HPI haut potentiel intellectuel - Trees By Bike









.jpg?itok=Yj-i787e)


.png)
