Dans l'océan des données qui nous submerge, quelques outils précieux nous permettent de naviguer et d'en extraire un sens. Moyenne, médiane, mode et écart-type, ces termes, souvent entendus, restent parfois mystérieux. Pourtant, leur compréhension est essentielle pour décrypter l'information et prendre des décisions éclairées.
Imaginez un tableau impressionniste. De près, une multitude de touches de couleur distinctes. De loin, une image cohérente se dessine. Les statistiques descriptives, dont font partie la moyenne, la médiane, le mode et l'écart-type, agissent comme un recul face à la complexité des données, nous permettant d'en saisir l'essence.
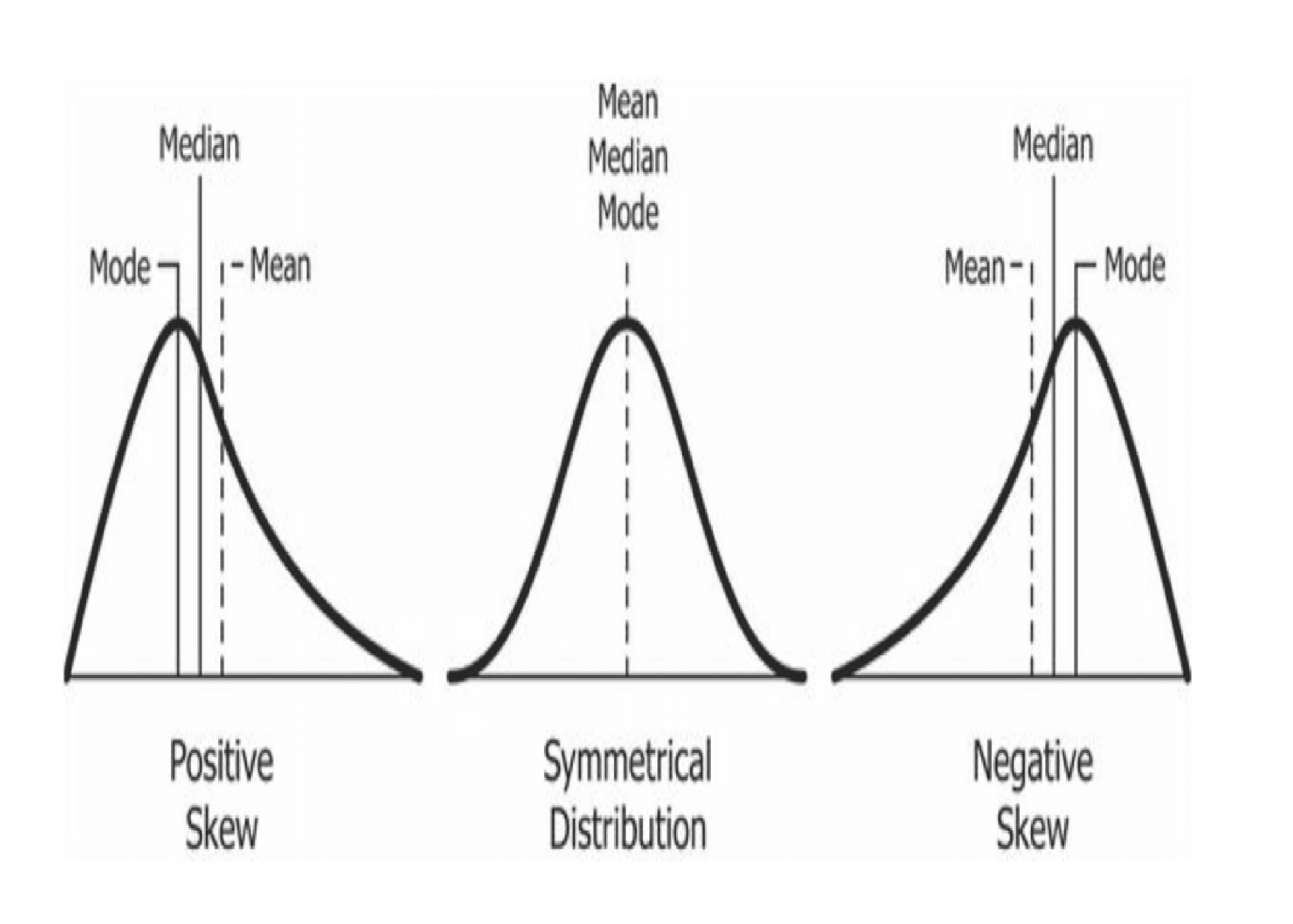
Mais que représentent exactement ces indicateurs statistiques ? La moyenne, résultat de la somme des valeurs divisée par leur nombre, offre une image globale de la tendance centrale. La médiane, valeur centrale d'une série ordonnée, est moins sensible aux valeurs extrêmes. Le mode, valeur la plus fréquente, indique la concentration des données. Enfin, l'écart-type mesure la dispersion des valeurs autour de la moyenne, révélant l'homogénéité ou l'hétérogénéité de l'ensemble.
Leur origine remonte aux travaux pionniers de mathématiciens et statisticiens comme Karl Pearson et Ronald Fisher, qui ont posé les bases de l'analyse statistique moderne. Ces outils, initialement utilisés pour des études démographiques et scientifiques, sont aujourd'hui omniprésents, de l'économie à la médecine, en passant par le marketing et la sociologie.
Maîtriser ces concepts est crucial pour éviter les interprétations erronées. Une moyenne élevée peut masquer de fortes inégalités, tandis qu'un écart-type important peut signaler une grande variabilité des données. L’utilisation conjointe de ces indicateurs offre une vision plus complète et nuancée de la réalité.
Prenons l'exemple des salaires dans une entreprise. La moyenne peut être tirée vers le haut par quelques salaires très élevés, alors que la médiane reflète davantage le salaire « typique ». Le mode, quant à lui, pourrait indiquer le salaire le plus couramment versé. L'écart-type permettra de mesurer les disparités salariales au sein de l'entreprise.
Ces outils statistiques offrent de nombreux avantages. Ils permettent de synthétiser des données complexes, de comparer des groupes et de détecter des tendances. Ils aident également à prendre des décisions éclairées en se basant sur des informations quantifiables.
Avantages et Inconvénients des Indicateurs Statistiques
| Indicateur | Avantages | Inconvénients |
|---|---|---|
| Moyenne | Facile à calculer, représentation globale | Sensible aux valeurs extrêmes |
| Médiane | Non influencée par les valeurs extrêmes | Ne prend pas en compte toutes les valeurs |
| Mode | Identifie la valeur la plus fréquente | Peut ne pas exister ou être multiple |
| Écart-type | Mesure la dispersion des données | Interprétation complexe sans la moyenne |
FAQ:
1. Qu'est-ce que la moyenne arithmétique? Réponse: La somme des valeurs divisée par le nombre de valeurs.
2. Comment calculer la médiane? Réponse: Ordonner les valeurs et trouver la valeur centrale.
3. Quand utiliser le mode? Réponse: Pour identifier la valeur la plus fréquente.
4. Qu'indique un écart-type élevé? Réponse: Une grande dispersion des données.
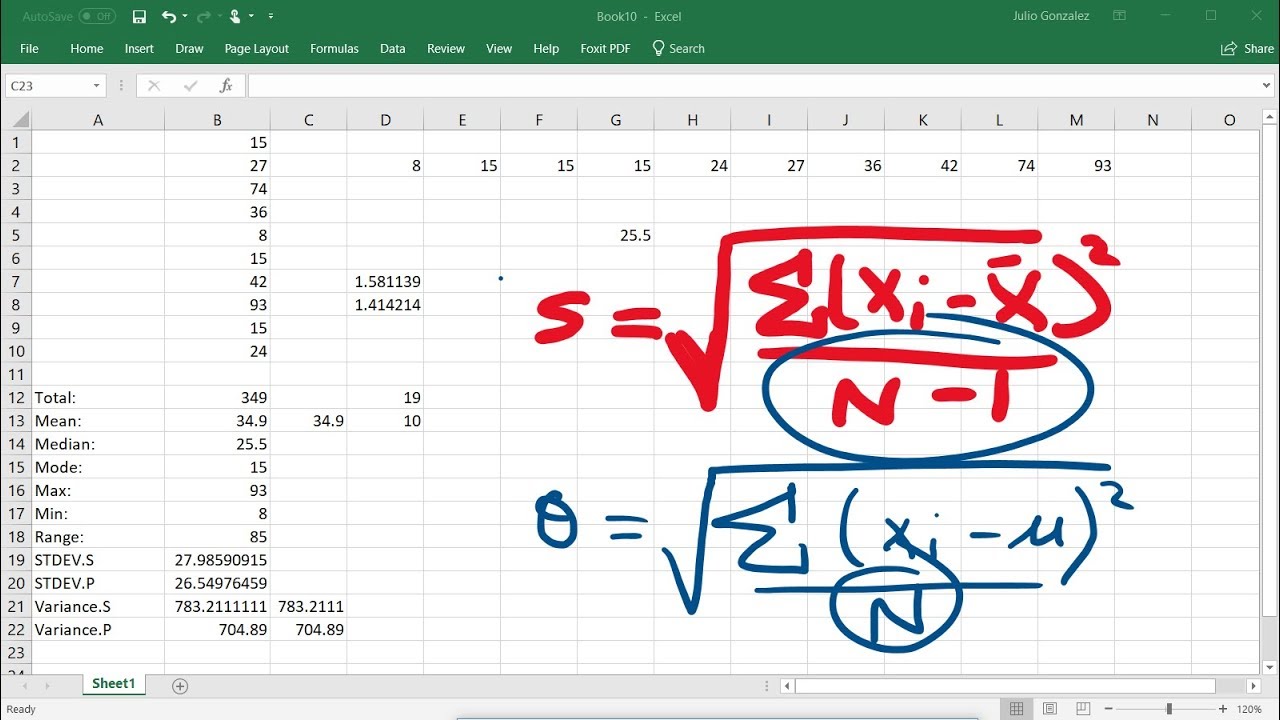
5. Qu'est-ce que la variance? Réponse: Le carré de l'écart-type.
6. Comment interpréter la distribution normale? Réponse: Une distribution symétrique autour de la moyenne.
7. Quel logiciel utiliser pour calculer ces indicateurs? Réponse: Excel, R, Python, etc.
8. Comment choisir le bon indicateur? Réponse: Dépend du type de données et de l'objectif de l'analyse.
En conclusion, la moyenne, la médiane, le mode et l’écart-type sont des outils essentiels pour comprendre et interpréter les données. Ils nous permettent de transformer des chiffres bruts en informations significatives et de prendre des décisions éclairées dans de nombreux domaines. Leur utilisation judicieuse, en tenant compte de leurs limites respectives, est la clé pour naviguer efficacement dans le monde complexe des données et en extraire toute la richesse. N'hésitez pas à approfondir ces concepts et à les appliquer à vos propres analyses pour en tirer pleinement profit.
Calculate Mean Age at Milford Sykes blog - Trees By Bike
Mean Median Mode On Graph - Trees By Bike
Probability Calculator Using Standard Deviation And Mean at Breanna - Trees By Bike
envidia Confusión sutil how to find mean median mode range and standard - Trees By Bike
Mean Median and Mode - Trees By Bike
How To Calculate Median Absolute Deviation In R - Trees By Bike
Calculating Mean Median Mode And Standard Deviation In Excel Youtube - Trees By Bike
mean median mode standard deviation - Trees By Bike
Mean Mode And Median Worksheets - Trees By Bike
Mean Median and Mode Explained with Examples - Trees By Bike
What Is A Range Math Definition at Holly Johnson blog - Trees By Bike
Standard Deviation Mean Median Mode - Trees By Bike
Calculate Variance Based On Standard Deviation at Sara Valle blog - Trees By Bike
How To Compare Range And Standard Deviation at Eric Zheng blog - Trees By Bike
Mean Median Mode Range Chart - Trees By Bike







.png)




