Dans l'univers parfois intimidant des statistiques, le concept de quartile peut sembler complexe. Pourtant, démystifier la méthode pour déterminer un quartile s'avère plus simple qu'il n'y paraît. Comprendre comment obtenir un quartile est une compétence essentielle pour analyser et interpréter des données, que ce soit pour vos études, votre travail, ou simplement pour mieux comprendre le monde qui vous entoure.
L'idée de diviser un ensemble de données en quatre parties égales, pour en analyser la dispersion et la répartition, est ancienne. L'utilisation des quartiles remonte aux premiers travaux de statistique descriptive, cherchant à résumer et à comprendre la distribution des données. La détermination d'un quartile permet de repérer les valeurs qui séparent les données en quarts, offrant ainsi une vision plus précise de la dispersion des valeurs autour de la médiane.
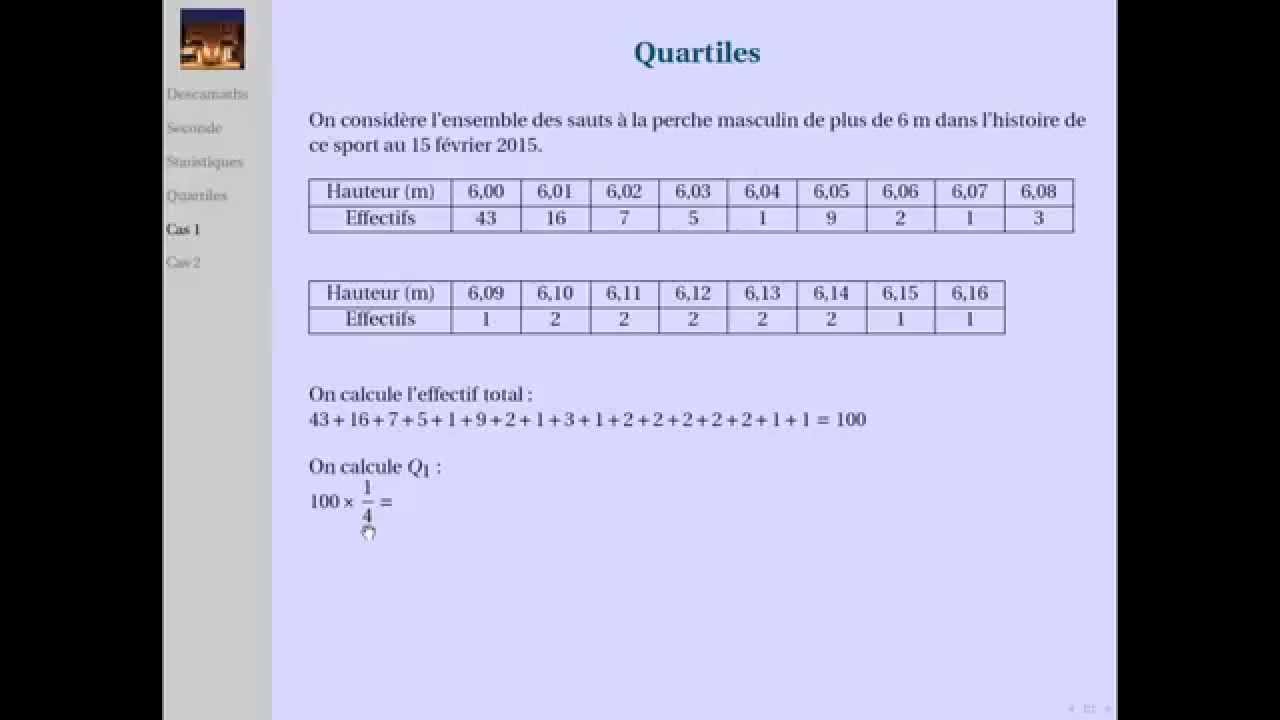
La méthode de calcul d'un quartile est fondamentale en statistique descriptive. Elle permet d'identifier les valeurs qui divisent un ensemble de données ordonnées en quatre parties égales. Le premier quartile (Q1) représente la valeur en dessous de laquelle se trouvent 25% des données. Le deuxième quartile (Q2), également appelé médiane, représente la valeur centrale de la distribution. Enfin, le troisième quartile (Q3) correspond à la valeur en dessous de laquelle se trouvent 75% des données. L'écart interquartile (Q3 - Q1) est une mesure de la dispersion des données autour de la médiane, moins sensible aux valeurs extrêmes que l'écart type.
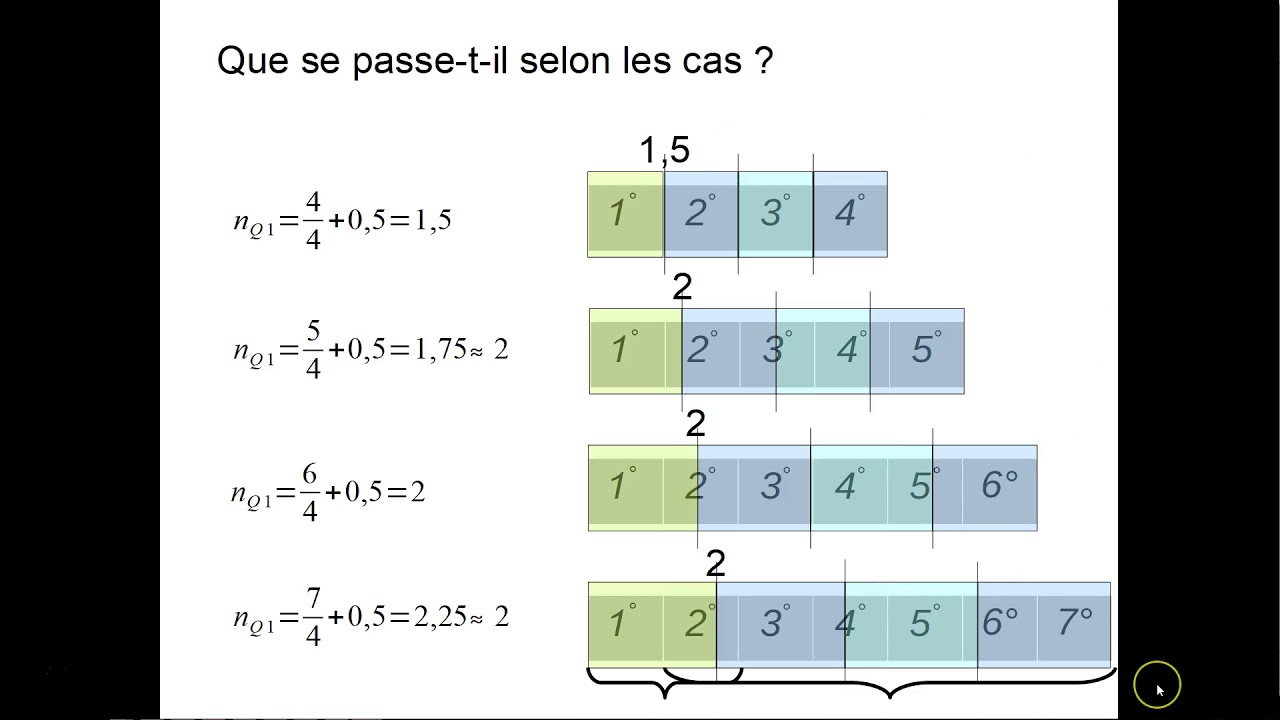
Un des problèmes récurrents lors du calcul d'un quartile est la gestion des ensembles de données avec un nombre pair ou impair de valeurs. Différentes méthodes existent, pouvant mener à des résultats légèrement différents. Il est crucial de choisir une méthode et de s'y tenir pour garantir la cohérence de l'analyse. Par exemple, certains logiciels utilisent une interpolation linéaire entre les valeurs, tandis que d'autres utilisent des méthodes d'arrondi. La compréhension de ces nuances est essentielle pour interpréter correctement les résultats.
Un autre défi réside dans la présence de valeurs extrêmes, qui peuvent influencer la position des quartiles et donner une image faussée de la distribution des données. Dans ce cas, l'utilisation de diagrammes en boîte (boxplots) peut s'avérer utile pour visualiser la dispersion des données et identifier les valeurs aberrantes.
Pour calculer un quartile, il faut d'abord ordonner les données de manière croissante. Ensuite, on identifie la médiane (Q2). Pour Q1, on prend la médiane de la première moitié des données (avant Q2). Pour Q3, on prend la médiane de la seconde moitié des données (après Q2).
Avantages du calcul des quartiles: 1. Mesure de la dispersion : Les quartiles permettent de mesurer la dispersion des données autour de la médiane. 2. Identification des valeurs extrêmes: L'écart interquartile aide à identifier les valeurs aberrantes. 3. Robustesse aux valeurs extrêmes: Contrairement à la moyenne et à l'écart type, les quartiles sont moins sensibles aux valeurs extrêmes.
Exemples : 1. Données : 2, 4, 6, 8, 10. Q1 = 4, Q2 = 6, Q3 = 8. 2. Données : 1, 3, 5, 7, 9, 11. Q1 = 3, Q2 = 6, Q3 = 9.
Avantages et Inconvénients du calcul des quartiles
| Avantages | Inconvénients |
|---|---|
| Mesure robuste de la dispersion | Peut masquer des détails importants de la distribution |
| Facile à comprendre et à interpréter | Différentes méthodes de calcul peuvent donner des résultats légèrement différents |
| Utile pour identifier les valeurs aberrantes | Ne prend pas en compte toutes les valeurs de la distribution |
FAQ : 1. Qu'est-ce qu'un quartile ? Réponse : Un quartile est une valeur qui divise un ensemble de données ordonnées en quatre parties égales. 2. Comment calculer Q1 ? Réponse : On calcule la médiane de la première moitié des données. 3. Comment calculer Q3 ? Réponse : On calcule la médiane de la seconde moitié des données.
En conclusion, savoir comment déterminer un quartile est un outil puissant pour analyser et interpréter des données. Comprendre le calcul d'un quartile vous permet de mieux appréhender la distribution des données, d'identifier les valeurs centrales et la dispersion autour de celles-ci. De la compréhension des données financières à l'analyse des résultats d'une enquête, maîtriser les quartiles ouvre la porte à une meilleure compréhension du monde chiffré qui nous entoure. N'hésitez pas à explorer davantage ce concept et à l'appliquer à vos propres analyses.
ᐉ Calculer le quartile dun jeu de données avec excel - Trees By Bike
comment calculer un quartile - Trees By Bike
Ferien Monopol Büste comment calculer écart type Tappen Scheibe Lauern - Trees By Bike
comment calculer un quartile - Trees By Bike
Comment calculer le périmètre d - Trees By Bike
Le diagramme de quartiles - Trees By Bike
comment calculer un quartile - Trees By Bike
Ntroduire 74 imagen formule quartile excel - Trees By Bike
Découvrir 77 imagen formule de variation des prix - Trees By Bike
Solicitante insalubre Atravesar comment calculer les quartiles - Trees By Bike
Quartile définition et explications - Trees By Bike
comment calculer un quartile - Trees By Bike
comment calculer un quartile - Trees By Bike
Comment Se Calcule Une Moyenne - Trees By Bike
Ntroduire 74 imagen formule quartile excel - Trees By Bike