Démystifier les Tangentes : Un Guide Complet sur le Tracé

20 Jul 2024
fr
Emil

comment tracer une tangente sur une courbe

Imaginez un instant un skieur dévalant une piste sinueuse. À chaque virage, sa trajectoire dessine une courbe, et à chaque instant précis de cette descente, une droite effleure la courbe, représentant la direction instantanée du skieur. Cette droite, c'est la tangente à la courbe. Loin d'être un concept abstrait réservé aux salles de classe, la capacité de déterminer et de tracer une tangente à une courbe trouve des applications dans une multitude de domaines, de la physique à l'économie, en passant par l'ingénierie et l'informatique.

Le concept de tangente est intimement lié à la notion de dérivée en mathématiques, qui quantifie le taux de variation instantané d'une fonction. En d'autres termes, la dérivée nous indique comment une grandeur change par rapport à une autre à un point précis. Or, la tangente à une courbe en un point donné est définie comme la droite dont la pente est égale à la valeur de la dérivée de la fonction en ce point.

L'histoire de la détermination des tangentes remonte à l'Antiquité, avec les travaux de géomètres grecs comme Euclide et Archimède. Cependant, ce sont les développements du calcul infinitésimal au XVIIe siècle, notamment grâce aux travaux de Pierre de Fermat, Isaac Newton et Gottfried Wilhelm Leibniz, qui ont permis une formalisation rigoureuse du concept de tangente et son lien avec la dérivée.

L'importance de savoir comment tracer une tangente sur une courbe est indéniable. En physique, par exemple, la tangente à la courbe de position d'un objet en mouvement nous donne sa vitesse instantanée. En économie, la tangente à une courbe de coût total peut être utilisée pour déterminer le coût marginal de production. En informatique graphique, les tangentes sont utilisées pour créer des courbes lisses et réalistes.

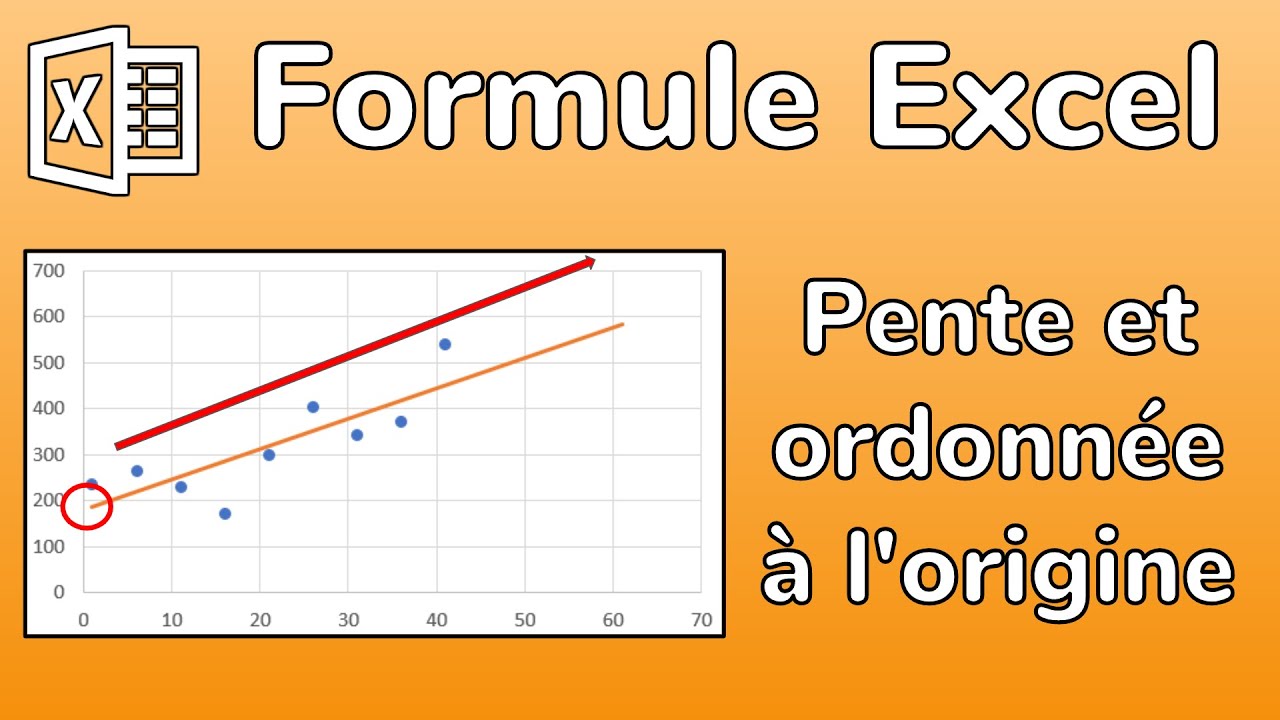
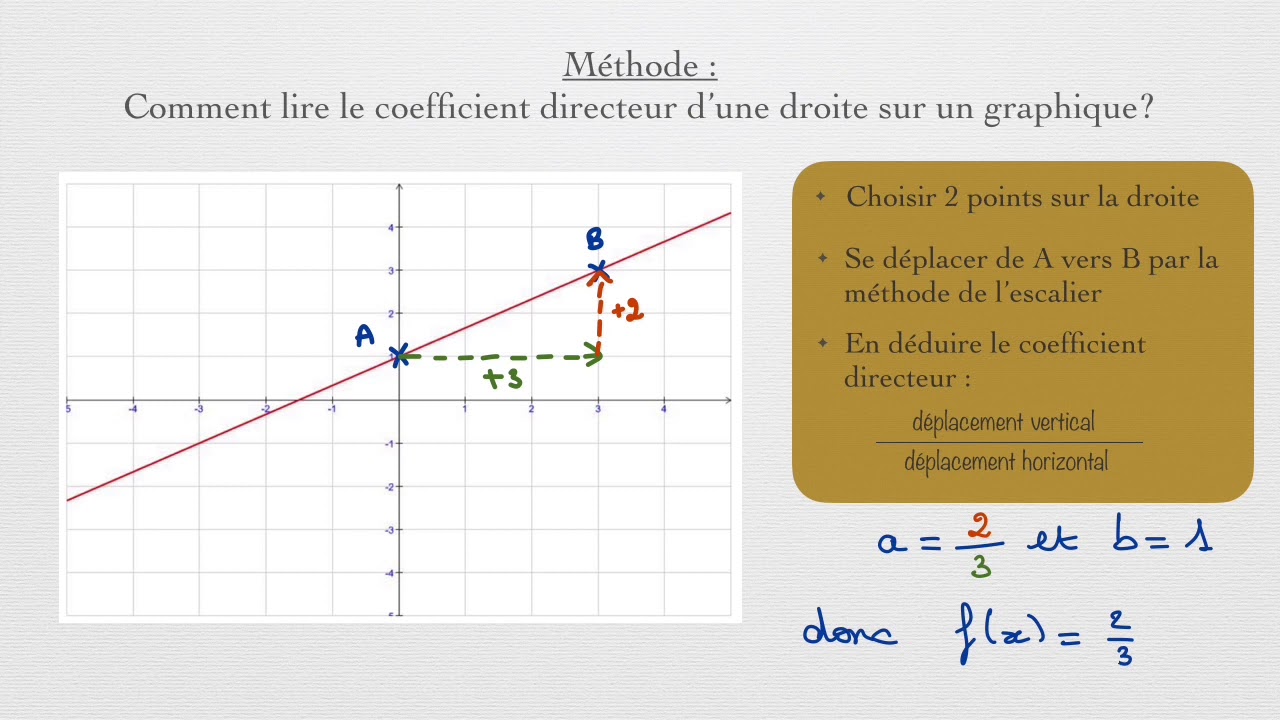
Pour tracer une tangente à une courbe en un point donné, nous devons d'abord déterminer la pente de la tangente en ce point. Pour ce faire, nous calculons la dérivée de la fonction qui représente la courbe en ce point. La dérivée nous donne la pente de la droite tangente. Une fois la pente connue, nous pouvons utiliser l'équation de la droite pour déterminer l'équation de la tangente. Par exemple, si la pente de la tangente est de 2 et que la tangente passe par le point (1,3), alors l'équation de la tangente est y = 2x + 1.

Bien sûr, il existe des cas particuliers et des situations plus complexes qui nécessitent des techniques plus avancées pour déterminer la tangente. Cependant, la compréhension fondamentale du lien entre la dérivée et la tangente est essentielle pour aborder ces problèmes.

En conclusion, la capacité de tracer une tangente à une courbe est une compétence essentielle dans de nombreux domaines. En comprenant le concept de dérivée et sa relation avec la tangente, nous pouvons résoudre une variété de problèmes pratiques et théoriques. La prochaine fois que vous observerez une courbe, que ce soit la trajectoire d'une balle de baseball ou la fluctuation d'un cours boursier, rappelez-vous que la tangente nous donne une perspective unique sur le changement instantané et nous permet de mieux comprendre le monde qui nous entoure.