Immaginate di entrare in una pasticceria. Vetra scintillante, profumi invitanti e una miriade di forme che stuzzicano la vista: torte a strati che si innalzano come piramidi, bignè rotondi come sfere, cannoli cilindrici ripieni di dolcezza. Ognuna di queste delizie, oltre ad essere un tripudio per il palato, rappresenta un esempio concreto di solido geometrico, figure che popolano il nostro mondo e che, nella terza media, diventano protagoniste di un avvincente viaggio di scoperta matematica.
Ma cosa sono esattamente questi "solidi geometrici" che tanto affascinano studenti e professori? Per dirla in modo semplice, sono figure geometriche che, a differenza dei loro "cugini" piatti come i triangoli o i quadrati, si sviluppano nelle tre dimensioni dello spazio: lunghezza, larghezza e altezza. Pensate a una scatola di biscotti: non è piatta come un foglio di carta, vero? Ecco, quella scatola è un solido, e più precisamente un parallelepipedo.
La storia dei solidi geometrici è antica quanto la civiltà umana. Già gli antichi Egizi, per costruire le loro maestose piramidi, dovevano avere una conoscenza approfondita di queste figure e delle loro proprietà. E che dire dei Greci? Matematici come Pitagora ed Euclide hanno dedicato la loro vita allo studio dei solidi, gettando le basi per la geometria che studiamo ancora oggi.
Ma perché i solidi geometrici sono così importanti? Perché ci aiutano a comprendere e descrivere il mondo che ci circonda. Pensate all'architettura, all'ingegneria, al design: tutte queste discipline si basano sulla conoscenza dei solidi e delle loro caratteristiche. Imparare a riconoscerli, classificarli e calcolarne il volume e la superficie non è solo un esercizio mentale, ma un bagaglio fondamentale per affrontare con successo il proprio percorso di studi e, in futuro, anche il mondo del lavoro.
Tuttavia, l'apprendimento dei solidi geometrici nella terza media può presentare alcune sfide. La visualizzazione tridimensionale, la comprensione delle formule e la risoluzione dei problemi pratici richiedono impegno, concentrazione e un pizzico di fantasia. Ma niente paura! Con la giusta dose di impegno e con l'aiuto di strumenti didattici innovativi, come software di modellazione 3D e video lezioni interattive, la geometria solida può trasformarsi da ostacolo insormontabile a materia stimolante e divertente.
Un esempio di come affrontare i solidi in modo pratico è quello di utilizzare oggetti di uso comune. Prendete un'arancia: ecco una sfera! Una scatola di latte? Un prisma rettangolare! Riconoscere i solidi negli oggetti di tutti i giorni aiuta a comprenderne meglio le caratteristiche e facilita l'apprendimento.
Vantaggi e Svantaggi dell'utilizzo di Risorse Online per l'apprendimento dei Solidi Geometrici
| Vantaggi | Svantaggi |
|---|---|
| Facilità di accesso a materiale didattico | Rischio di distrazione da parte di internet |
| Possibilità di apprendimento interattivo con video e animazioni | Necessità di un dispositivo elettronico e di una connessione internet |
| Disponibilità di esercizi online con correzione automatica | Mancanza di un'interazione diretta con l'insegnante |
Ricordate, la geometria solida non è un mostro a tre teste! Con un po' di pazienza, curiosità e la giusta dose di impegno, anche voi potrete diventare degli esperti "costruttori" di conoscenza nel magico mondo dei solidi geometrici.
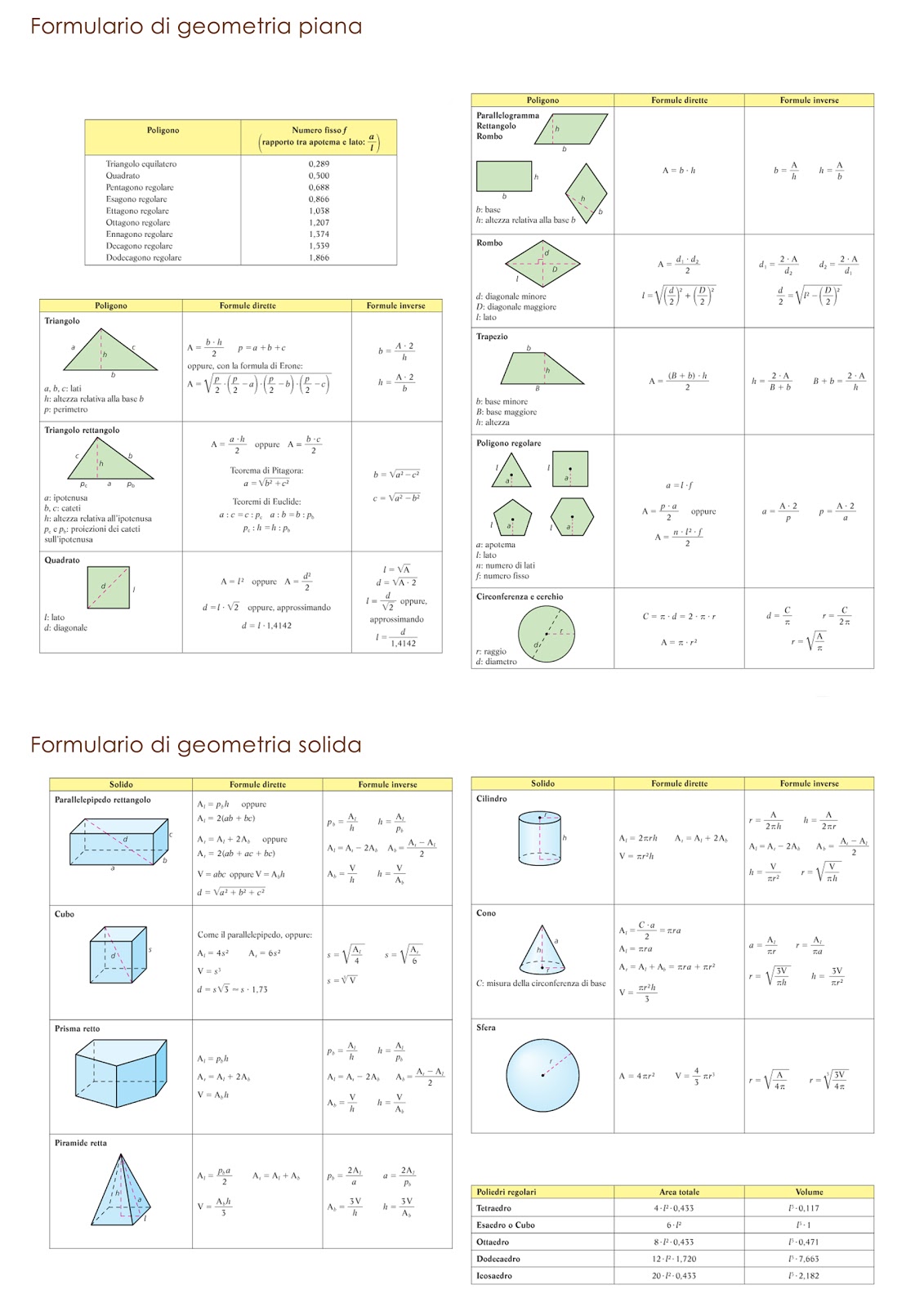
Formulario di geometria solida e piana - Trees By Bike
I solidi online worksheet for 2 primaria. You can do the exercises - Trees By Bike
Formule Dei Solidi Terza Media - Trees By Bike
i solidi terza media pdf - Trees By Bike
Geometria Solida Volumi E Superfici Delle Principali BD9 - Trees By Bike
Formulario Geometria Solida per Medie - Trees By Bike
an image of different shapes in spanish - Trees By Bike
Problemi svolti sui solidi composti, geometria terza media - Trees By Bike
i solidi terza media pdf - Trees By Bike
i solidi terza media pdf - Trees By Bike
Esercizi Prima Legge Di Ohm Terza Media Svolti PDF Soluzioni - Trees By Bike
Problemi svolti sui solidi composti, geometria terza media - Trees By Bike
ANTEPRIMA DI UN ESERCIZIO SVOLTO SUI SOLIDI DI ROTAZIONE (TERZA MEDIA - Trees By Bike
i solidi terza media pdf - Trees By Bike
Formulario de geometría - Trees By Bike