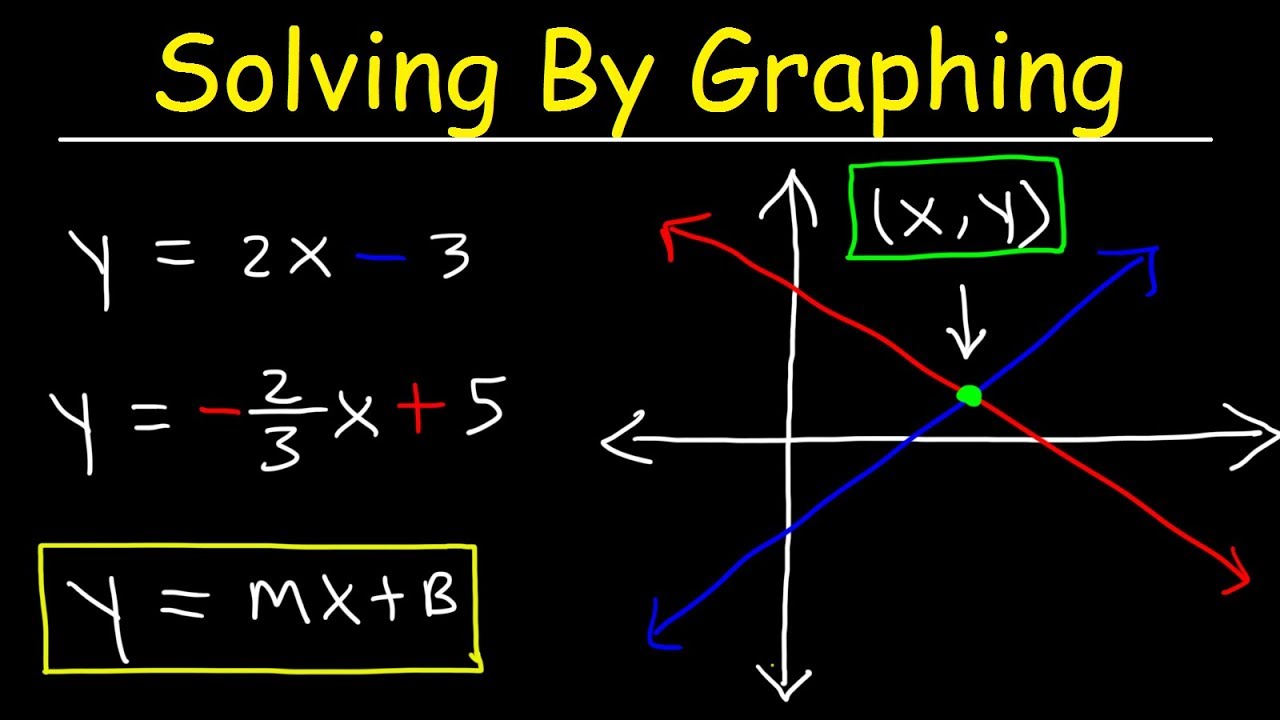
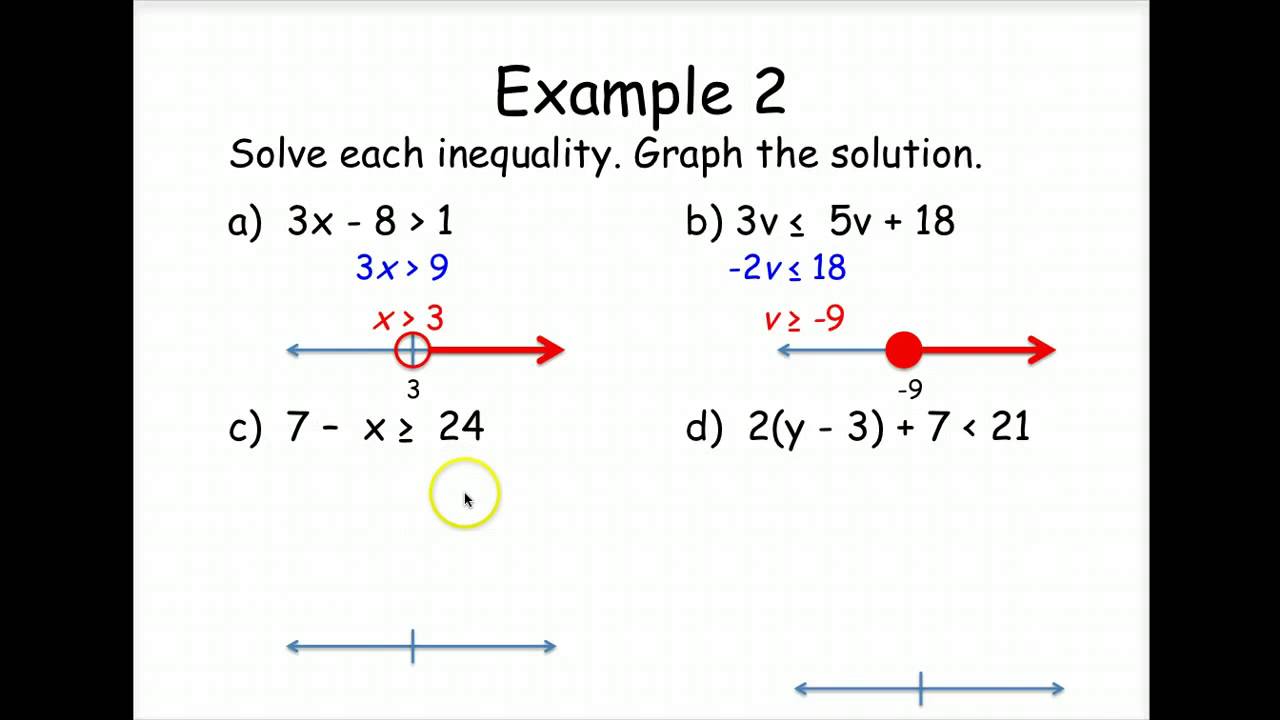
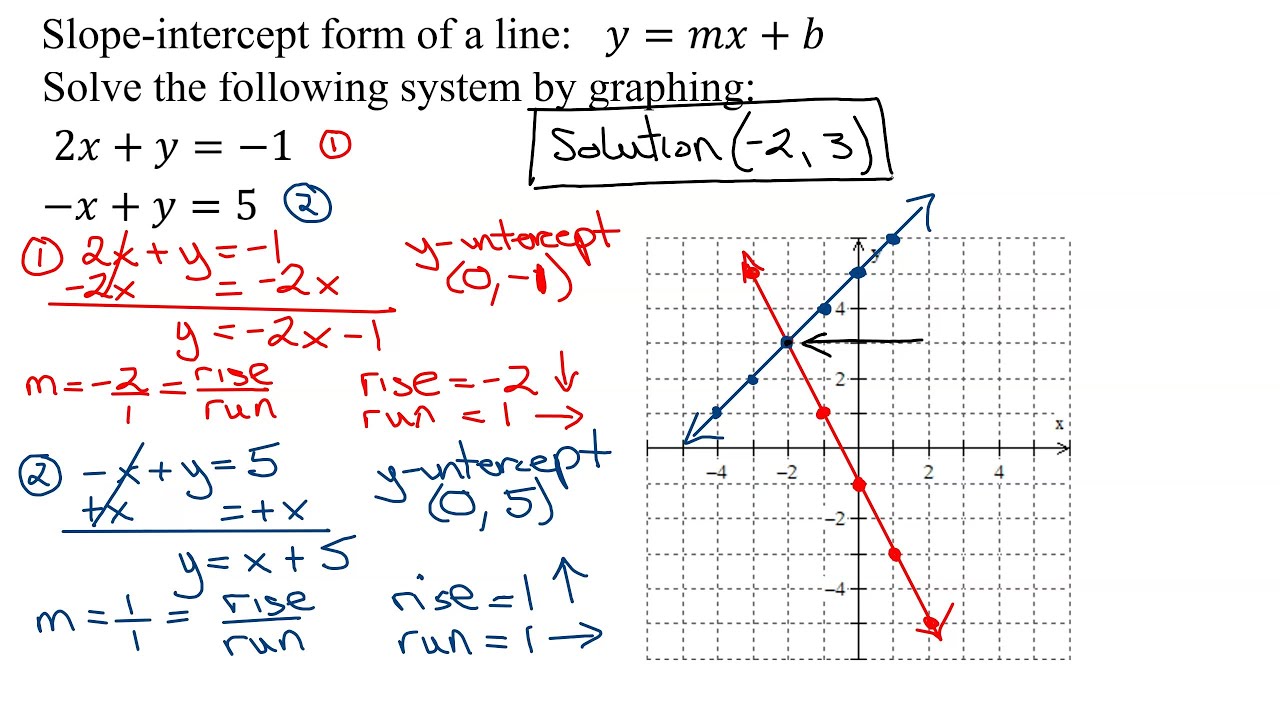
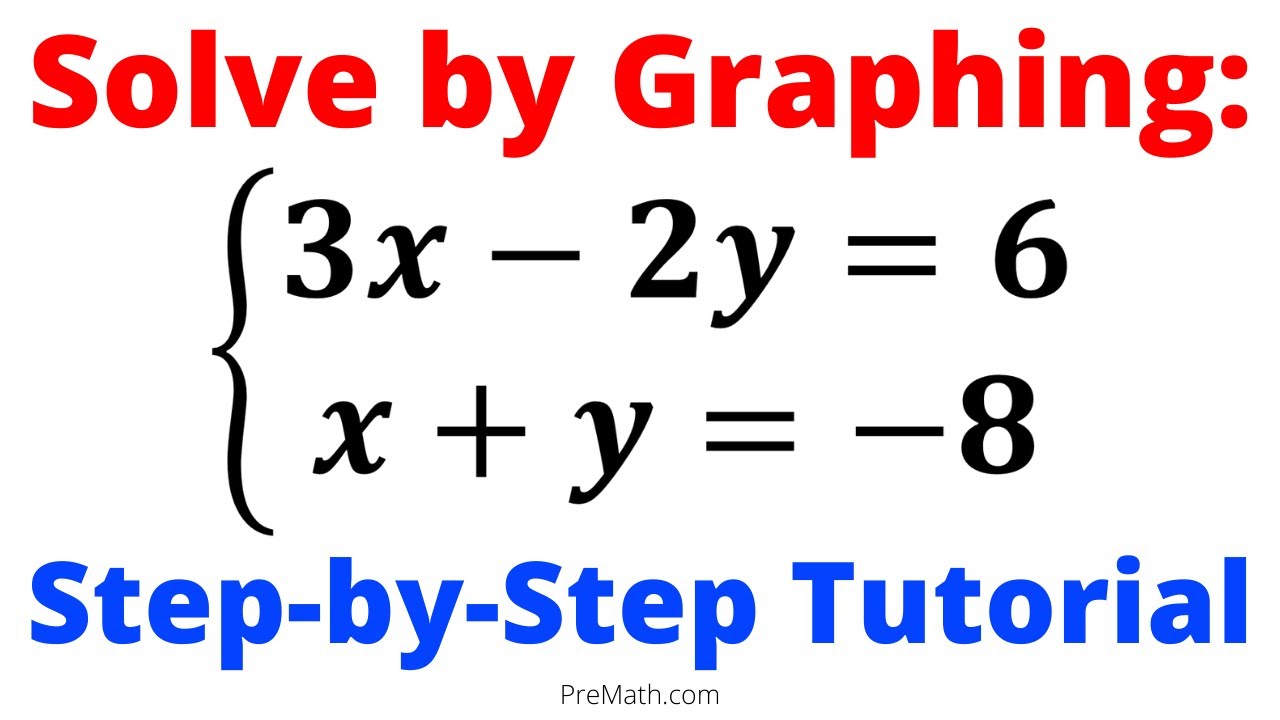Come Risolvere un Sistema di Equazioni col Metodo Grafico

18 Jun 2024
it
Emil

Avete presente quando vi trovate davanti a due equazioni e vi sembra di essere finite in un labirinto di numeri? Niente panico, ragazze! Oggi vi sveliamo un trucco infallibile: risolvere un sistema di equazioni col metodo grafico.

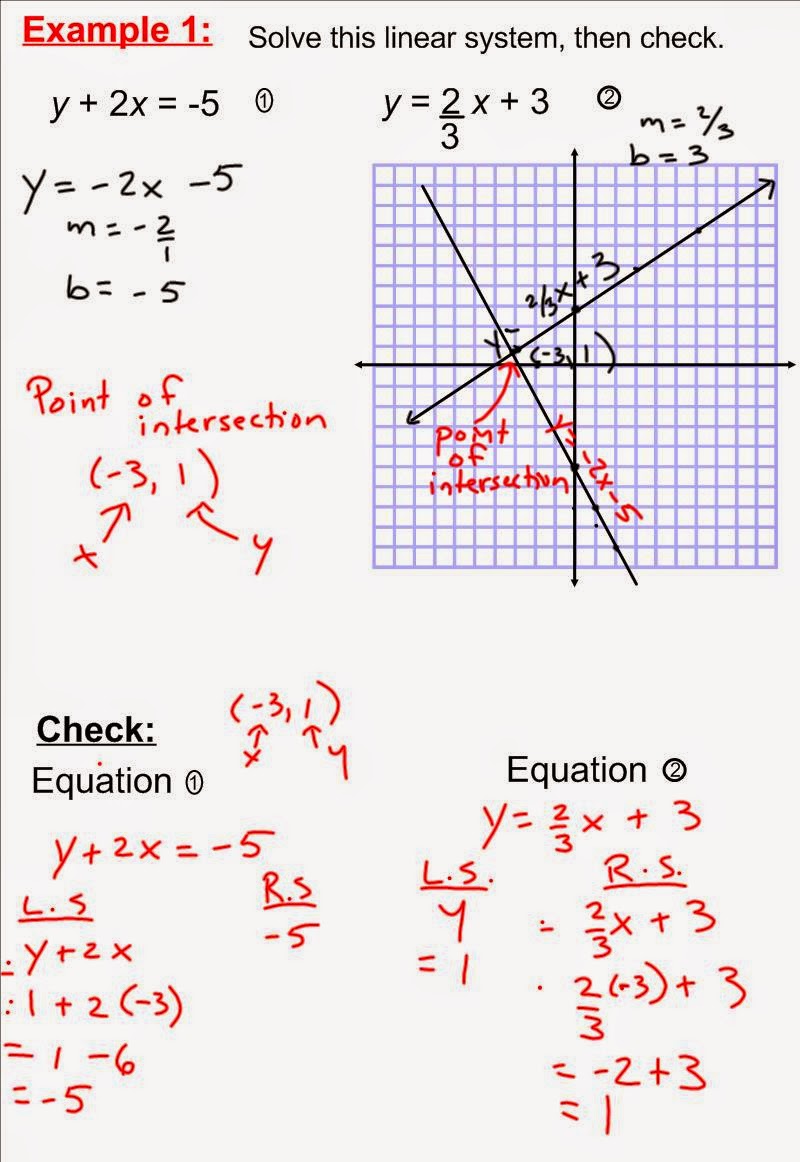
Immaginate di avere due strade che si incrociano in un punto preciso. Ecco, le equazioni sono come quelle strade e il punto d'incontro è la soluzione che cerchiamo. Con il metodo grafico, possiamo visualizzare tutto questo su un piano cartesiano e trovare la soluzione in un batter d'occhio!

Questo metodo, utilizzato da secoli dai matematici, offre un approccio visivo e intuitivo alla risoluzione di sistemi di equazioni lineari. Invece di perdersi in calcoli complicati, basta tracciare le rette corrispondenti alle equazioni e osservare dove si incontrano.

Naturalmente, come ogni tecnica, anche il metodo grafico ha i suoi limiti. La precisione del risultato dipende dalla cura con cui disegniamo le rette e dalla scala utilizzata. Tuttavia, rimane uno strumento potente per avere un'idea immediata della soluzione e per verificare i risultati ottenuti con altri metodi algebrici.

Pronte a scoprire tutti i segreti di questo metodo? Continuate a leggere e diventerete delle vere esperte nella risoluzione grafica dei sistemi di equazioni!

Vantaggi e Svantaggi del Metodo Grafico

Vantaggi	Svantaggi
Intuitivo e facile da visualizzare	Precisione limitata, soprattutto per soluzioni non intere
Utile per verificare soluzioni ottenute con altri metodi	Richiede tempo per disegnare accuratamente i grafici
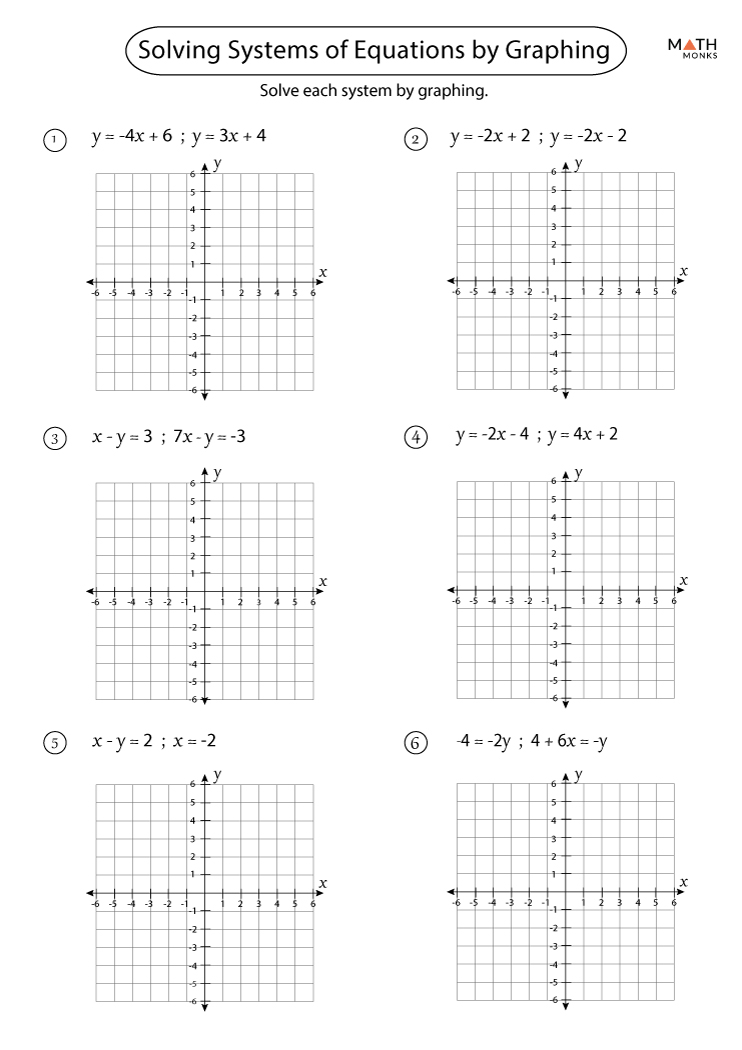
Adatto a sistemi di due equazioni in due incognite	Non ideale per sistemi con più di due incognite

5 Migliori Pratiche per il Metodo Grafico

Ecco alcuni consigli per applicare al meglio il metodo grafico:

Utilizzare un piano cartesiano preciso: Assicurarsi che gli assi siano ben definiti e che la scala sia adeguata per rappresentare accuratamente le rette.
Tracciare le rette con precisione: Scegliere almeno due punti per ogni retta e unirli con una linea retta e precisa.
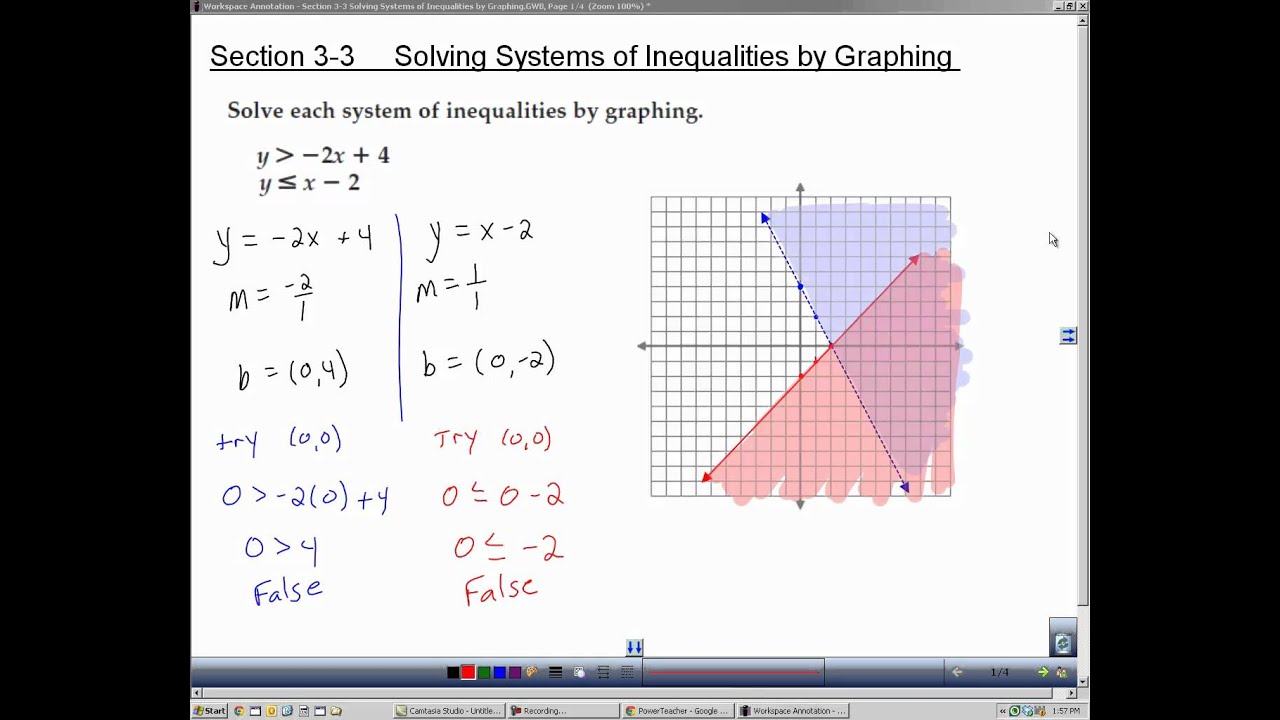
Individuare il punto di intersezione: Se le rette si intersecano, il punto di incontro rappresenta la soluzione del sistema.
Verificare la soluzione: Sostituire le coordinate del punto di intersezione nelle equazioni originali per assicurarsi che le soddisfino.
Interpretare i casi particolari: Se le rette sono parallele, il sistema non ha soluzione. Se le rette coincidono, il sistema ha infinite soluzioni.

Domande Frequenti sul Metodo Grafico

Ecco alcune domande comuni sul metodo grafico:

Posso usare il metodo grafico per qualsiasi sistema di equazioni?
Il metodo grafico è più adatto a sistemi di due equazioni lineari in due incognite. Diventa più complesso da applicare con più incognite.
Cosa succede se le rette non si intersecano?
Se le rette sono parallele, non si intersecano e il sistema non ha soluzione. Ciò indica che le equazioni sono incompatibili.

Consigli e Trucchi per il Metodo Grafico

Ecco alcuni consigli extra per semplificare il processo:

* Utilizzare colori diversi per le rette per una migliore visualizzazione.

* Segnare chiaramente il punto di intersezione e le sue coordinate.

* Praticare con diversi esempi per acquisire sicurezza.

In conclusione, il metodo grafico offre un modo intuitivo e visivamente efficace per risolvere sistemi di equazioni lineari. Sebbene la sua precisione possa essere limitata e sia più adatto a sistemi semplici, rimane uno strumento prezioso per comprendere il concetto di soluzione di un sistema e per verificare i risultati ottenuti con altri metodi. Con la pratica e i giusti accorgimenti, il metodo grafico può diventare un valido alleato nella risoluzione dei vostri problemi matematici!