Decodificare la complessità: Il diagramma di Venn A ∩ B ∩ C

14 Aug 2024
it
Emil

Immaginate di dover organizzare un'enorme quantità di dati, cercando di individuare le connessioni nascoste tra diversi gruppi di informazioni. Un compito arduo, non credete? Eppure, esiste uno strumento semplice ma potente che può aiutarci in questo compito: il diagramma di Venn.

In questo articolo, ci addentreremo nel cuore dei diagrammi di Venn a ∩ b ∩ c, esplorandone le origini, i principi fondamentali e le molteplici applicazioni. Scopriremo come questa rappresentazione grafica, apparentemente elementare, possa rivelarsi sorprendentemente efficace nell'affrontare problemi complessi in vari ambiti, dalla matematica alla logica, dalla statistica all'informatica.

Preparatevi ad immergervi nel mondo affascinante dei diagrammi di Venn e a scoprire come la loro semplicità possa illuminare anche le situazioni più intricate.

Il diagramma di Venn, come lo conosciamo oggi, fu formalizzato dal matematico inglese John Venn nel XIX secolo. Tuttavia, le sue radici affondano in concetti logici e matematici molto più antichi. Già nel XIII secolo, il filosofo e logico francese Ramon Llull utilizzava diagrammi circolari per rappresentare relazioni tra concetti.

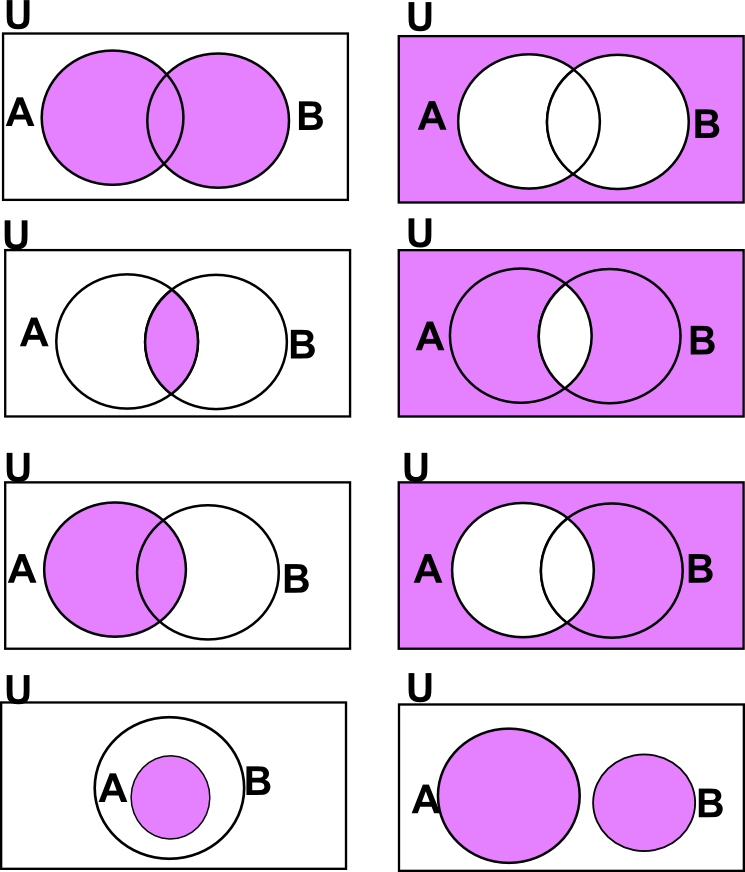
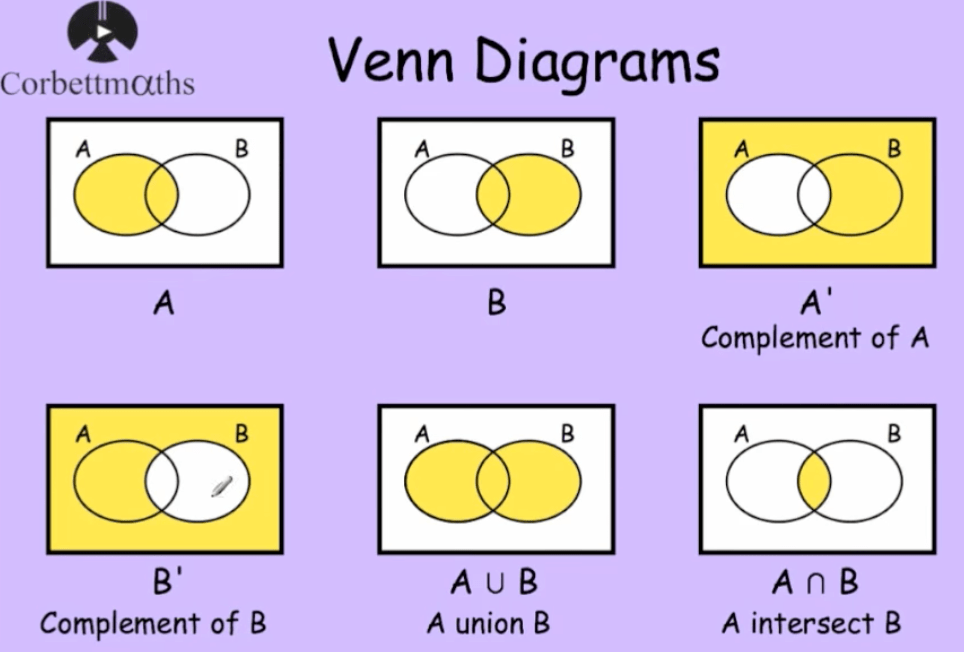
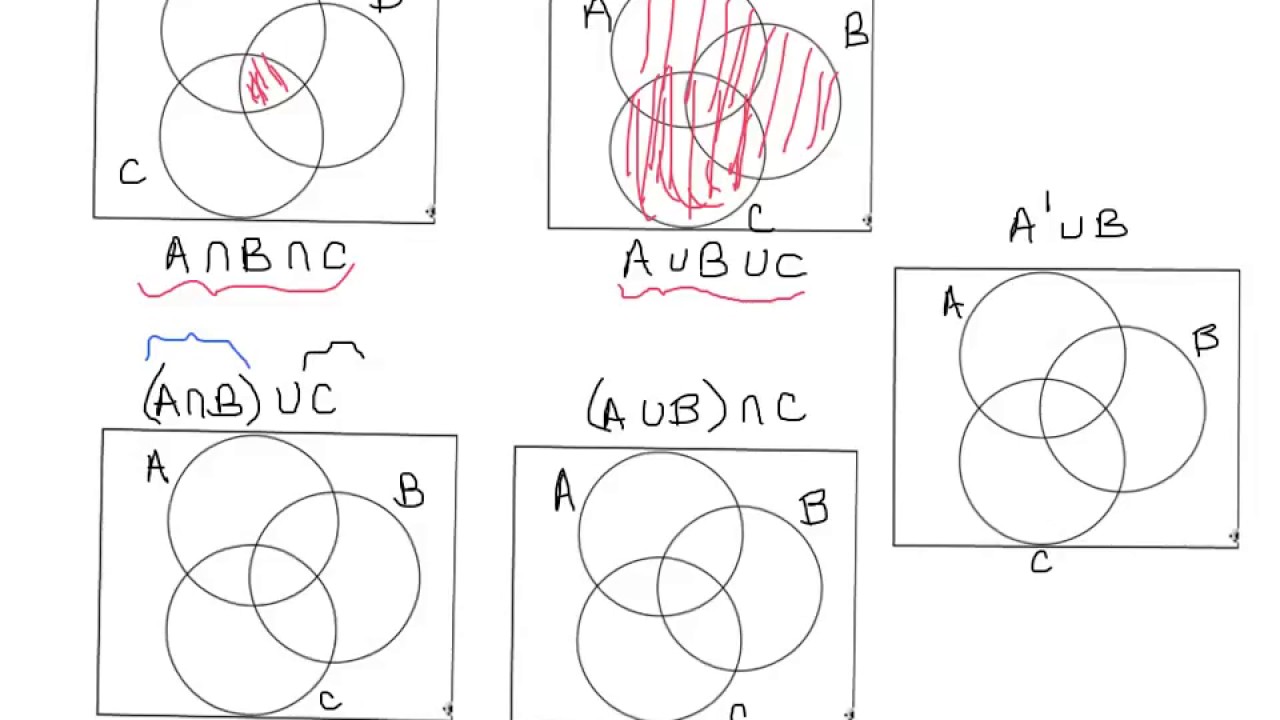
Il diagramma di Venn a ∩ b ∩ c è una rappresentazione grafica che illustra le relazioni tra tre insiemi: A, B e C. Ogni insieme è rappresentato da un cerchio e l'area in cui i cerchi si sovrappongono indica gli elementi che appartengono a più di un insieme.

Ad esempio, l'area dove tutti e tre i cerchi si sovrappongono rappresenta l'intersezione dei tre insiemi, ovvero gli elementi che appartengono contemporaneamente ad A, B e C (A ∩ B ∩ C).

Vantaggi e svantaggi del diagramma di Venn a ∩ b ∩ c

Come ogni strumento, anche il diagramma di Venn ha i suoi punti di forza e di debolezza. Vediamoli in dettaglio:

Vantaggi	Svantaggi
Chiarezza visiva	Difficoltà con insiemi numerosi
Semplicità d'uso	Rappresentazione limitata a pochi insiemi
Utilità in diversi ambiti	Possibilità di interpretazioni errate

Nonostante i suoi limiti, il diagramma di Venn a ∩ b ∩ c rimane uno strumento valido per visualizzare e comprendere le relazioni tra insiemi in modo semplice ed intuitivo.

I diagrammi di Venn a ∩ b ∩ c trovano applicazioni in vari ambiti:

Nella teoria degli insiemi, per visualizzare operazioni tra insiemi come unione, intersezione e complemento.
Nella logica, per rappresentare relazioni tra proposizioni e argomenti.
Nella statistica, per analizzare la distribuzione di dati in gruppi e sottogruppi.

Un esempio concreto dell'utilizzo dei diagrammi di Venn a ∩ b ∩ c è la classificazione di specie animali in base alle loro caratteristiche. Immaginiamo tre insiemi: A (animali che volano), B (animali che depongono le uova) e C (animali che vivono in acqua). Il diagramma di Venn ci permette di visualizzare facilmente le diverse combinazioni di queste caratteristiche, identificando ad esempio gli animali che volano, depongono le uova e vivono in acqua (A ∩ B ∩ C), come ad esempio alcuni tipi di uccelli acquatici.

In conclusione, il diagramma di Venn a ∩ b ∩ c è uno strumento potente e versatile, capace di semplificare la comprensione di relazioni complesse tra insiemi. Nonostante i suoi limiti, la sua intuitività e la sua chiarezza visiva lo rendono uno strumento prezioso in molteplici discipline. La prossima volta che vi troverete ad affrontare un problema che coinvolge la sovrapposizione di informazioni, ricordatevi del potere dei diagrammi di Venn: la soluzione potrebbe essere a portata di cerchio.