Chi l'ha detto che la geometria debba essere noiosa? Dimenticate i rigidi teoremi e le formule a memoria, perché il cerchio, con la sua perfezione senza tempo, è una fonte inesauribile di fascino e di sfide intellettuali. Che siate studenti alle prese con i compiti a casa o semplicemente curiosi di scoprire i segreti di questa figura geometrica, vi accompagneremo in un viaggio alla scoperta dei metodi per risolvere i problemi del cerchio.
Immaginate di dover organizzare un elegante cocktail party nel vostro giardino: come calcolare la superficie ideale per il vostro gazebo circolare? O forse state progettando un nuovo logo per il vostro brand e desiderate inserire un cerchio armonioso? La capacità di risolvere i problemi del cerchio si rivela essenziale in innumerevoli situazioni, dalla vita quotidiana alle applicazioni più complesse.
Fin dall'antichità, il cerchio ha affascinato matematici e filosofi, diventando un simbolo di perfezione, eternità e ciclicità. Pensate alla ruota, invenzione rivoluzionaria che ha cambiato il corso della storia, o all'orologio, che scandisce il tempo inesorabile con il suo moto circolare. La comprensione delle proprietà del cerchio ha permesso all'uomo di progredire in molteplici campi, dall'architettura all'ingegneria, dalla fisica all'astronomia.
Tuttavia, nonostante la sua apparente semplicità, il cerchio nasconde insidie e complessità che possono mettere a dura prova anche le menti più brillanti. Calcolare l'area di un settore circolare, determinare la lunghezza di una corda o risolvere problemi che coinvolgono angoli al centro e alla circonferenza richiede la conoscenza di formule specifiche e la capacità di applicarle correttamente.
Ma non temete! Questa guida vi fornirà gli strumenti necessari per affrontare con sicurezza qualsiasi problema legato al cerchio. Imparerete a destreggiarvi tra formule, teoremi e applicazioni pratiche, scoprendo come la geometria possa essere non solo utile, ma anche incredibilmente affascinante.
Vantaggi e Svantaggi della padronanza del cerchio
| Vantaggi | Svantaggi |
|---|---|
| Maggiore sicurezza nelle applicazioni pratiche | Rischio di confondere le formule |
| Sviluppo del pensiero logico e matematico | Necessità di esercizio costante |
| Apprezzamento per la bellezza e l'armonia della geometria | Difficoltà nell'affrontare problemi complessi senza una solida base matematica |
Con una conoscenza approfondita del cerchio e delle sue proprietà, sarete pronti ad affrontare qualsiasi sfida geometrica con stile e sicurezza. Ricordate, la geometria non è solo una materia scolastica, ma un linguaggio universale che descrive il mondo che ci circonda.
Area Of A Circle - Trees By Bike
how to solve circle problems - Trees By Bike
Angles Outside Of Circles - Trees By Bike
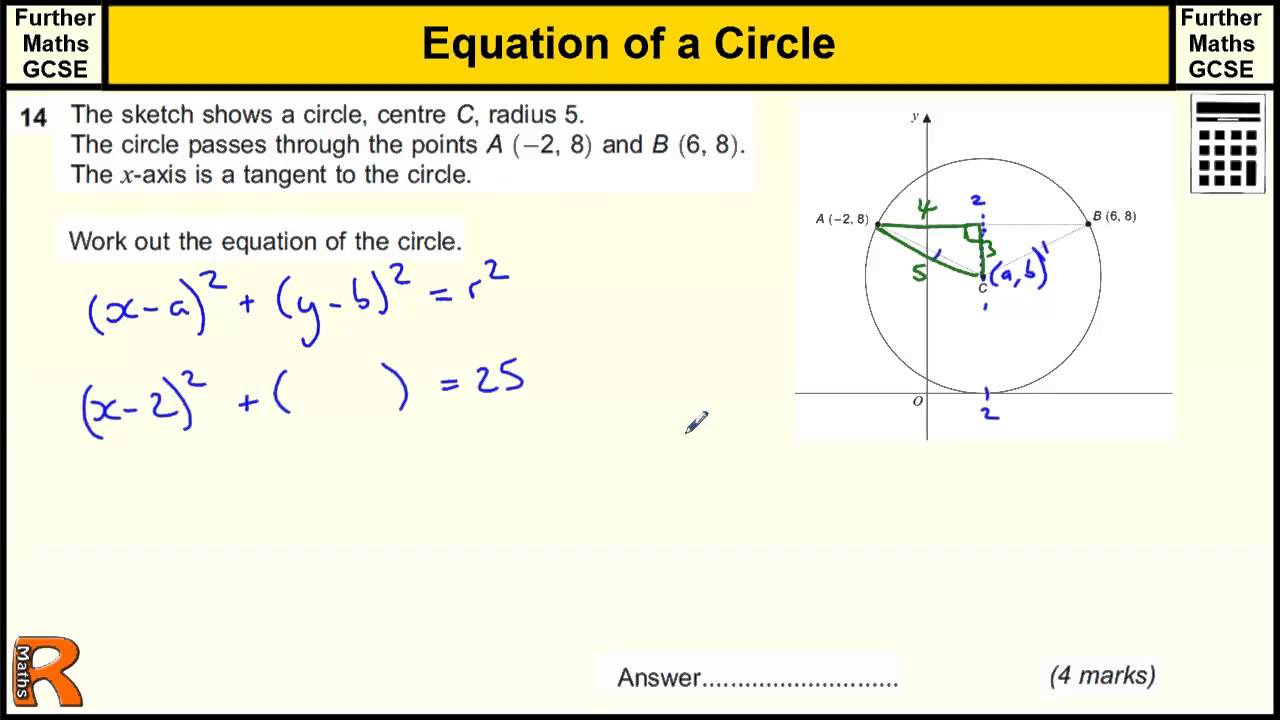
How To Solve For The Equation Of A Circle - Trees By Bike
Parts Of A Circle Word Problems - Trees By Bike
Equations Of Circles Practice - Trees By Bike
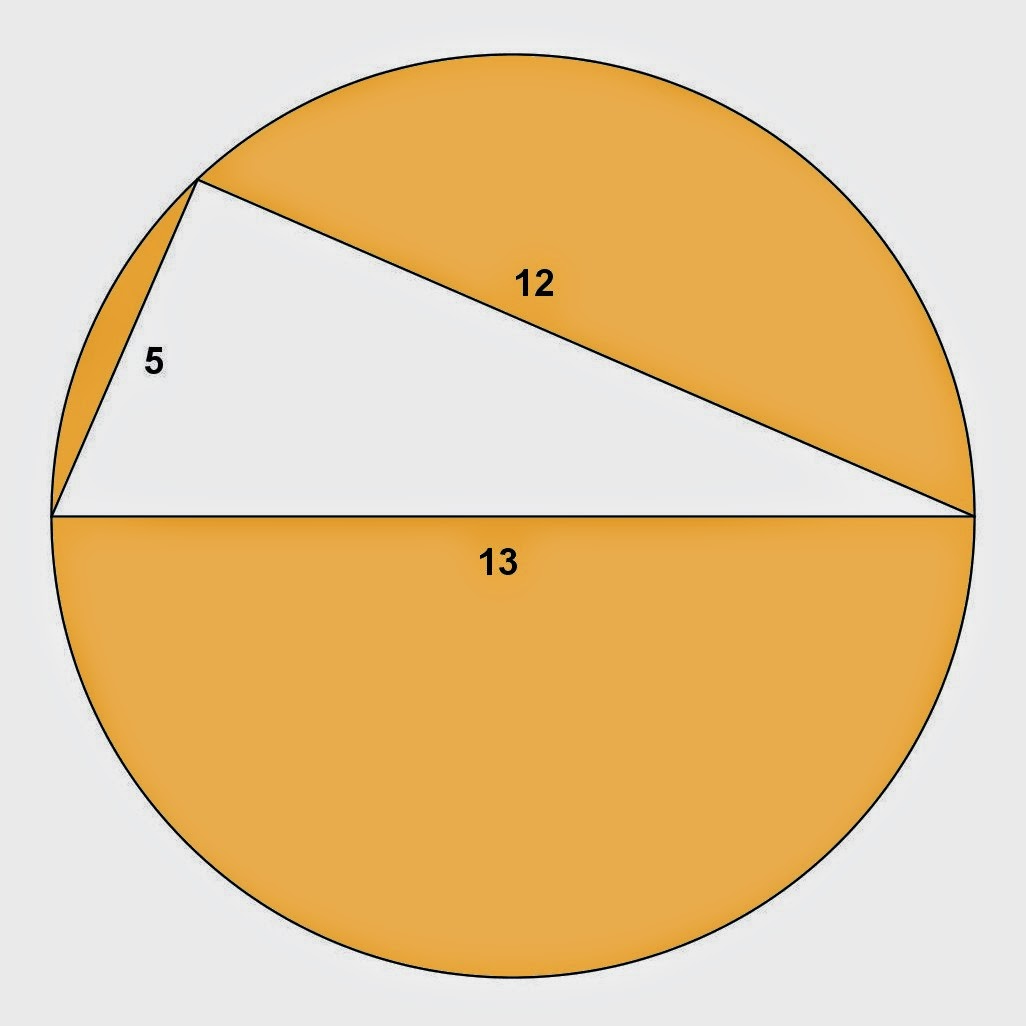
Math Principles: Triangle Inscribed in a Circle Problems, 2 - Trees By Bike
Area Of A Circle Word Problems - Trees By Bike
ACT Math: How to Solve Circle Problems - Trees By Bike
How to Solve Area of a Circle Word Problems. « Math :: WonderHowTo - Trees By Bike
Solve Problems Using Circle Theorems - Trees By Bike
Circle Theorems Practice Questions - Trees By Bike
Area of 2D Shapes - Trees By Bike
Solve Trigonometric Equations Using the Unit Circle - Trees By Bike
Math Principles: Triangle Inscribed in a Circle Problems, 2 - Trees By Bike