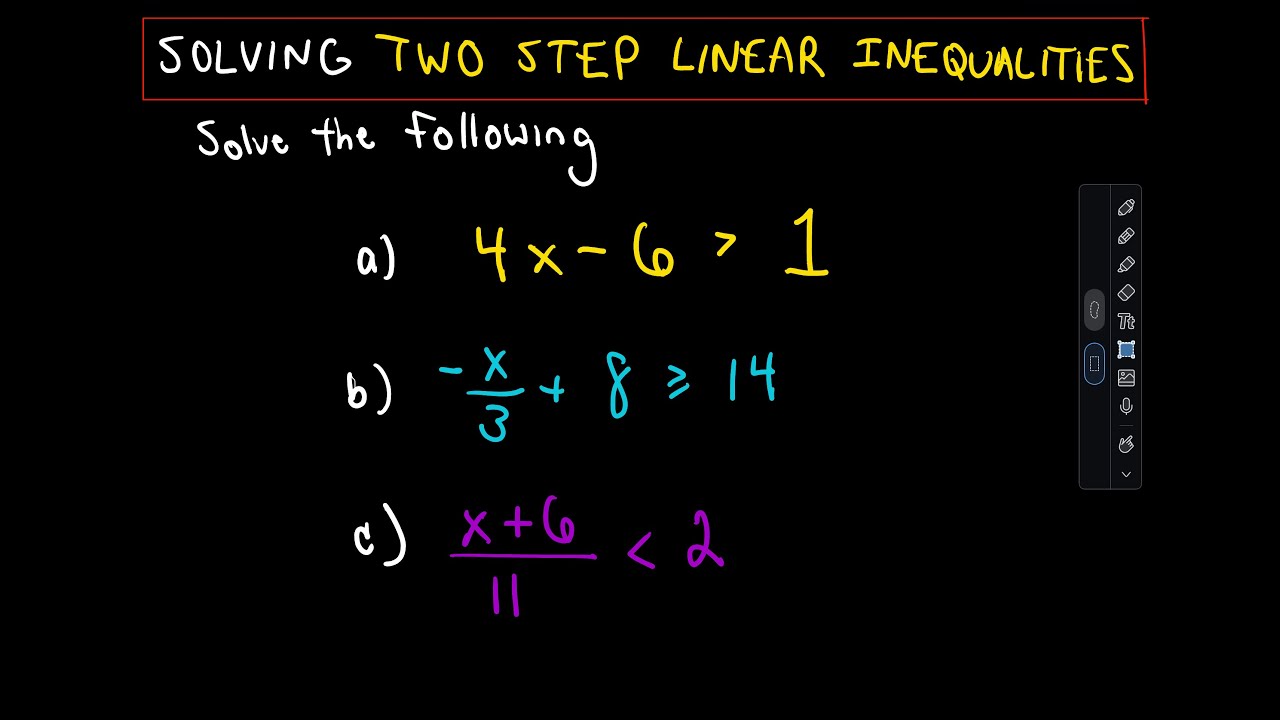Risolvere le disuguaglianze a due passi: La tua chiave per il successo matematico

04 Sep 2024
it
Emil

Avete mai incontrato un problema matematico che sembrava un enigma da decifrare? Un problema che richiedeva più di un semplice calcolo? Le disuguaglianze a due passi sono proprio questo: un rompicapo stimolante che, una volta risolto, apre le porte a una comprensione più profonda della matematica.

Ma non temete, perché questa guida è qui per accompagnarvi passo dopo passo nel mondo delle disuguaglianze a due passi, fornendovi tutti gli strumenti necessari per affrontarle con sicurezza. Dimenticate la frustrazione e la confusione, perché insieme trasformeremo le disuguaglianze a due passi da un ostacolo in un'opportunità per imparare e crescere.

Prima di immergerci nel vivo della questione, facciamo un passo indietro e definiamo cosa intendiamo con "disuguaglianze a due passi". Immagina una bilancia, dove da un lato hai un'espressione algebrica e dall'altro un valore numerico. Il segno di disuguaglianza (>, <, ≥, ≤) funge da perno, indicando quale lato è maggiore, minore o uguale all'altro. Risolvere una disuguaglianza a due passi significa trovare i valori della variabile che rendono vera la disuguaglianza, il che richiede due operazioni matematiche.

Le disuguaglianze a due passi non sono solo un concetto astratto confinato ai libri di testo, ma trovano applicazione in situazioni reali. Pensate, ad esempio, a un budget limitato per un progetto: la disuguaglianza a due passi vi aiuterà a determinare la quantità massima di denaro che potete spendere per ogni voce. Oppure, immaginate di dover organizzare un evento e di avere un numero limitato di posti disponibili: le disuguaglianze a due passi vi permetteranno di calcolare quanti biglietti potete vendere a un determinato prezzo per raggiungere il vostro obiettivo di guadagno.

Padroneggiare le disuguaglianze a due passi vi fornirà una solida base per affrontare concetti matematici più avanzati in futuro. Vi aiuterà a sviluppare capacità di pensiero critico, problem-solving e ragionamento logico, abilità preziose non solo in ambito accademico, ma anche nella vita di tutti i giorni.

Vantaggi e svantaggi di utilizzare le schede di lavoro per le disuguaglianze a due passaggi

Vantaggi	Svantaggi
Pratica mirata	Ripetitività
Verifica immediata dell'apprendimento	Limitazione nella creatività
Adatto a diversi stili di apprendimento	Possibile mancanza di contesto reale

Sebbene le schede di lavoro offrano numerosi vantaggi, è importante utilizzarle come strumento complementare ad altre attività di apprendimento. Integrare le schede di lavoro con esempi del mondo reale, discussioni in classe e attività di gruppo può arricchire l'esperienza di apprendimento e rendere le disuguaglianze a due passi più significative per gli studenti.

Cinque best practice per implementare le schede di lavoro per le disuguaglianze a due passaggi:

Iniziare con una revisione dei concetti di base: Assicurarsi che gli studenti abbiano una solida conoscenza delle disuguaglianze a un passo e delle operazioni algebriche di base prima di introdurre le disuguaglianze a due passaggi.
Introdurre il concetto in modo graduale: Iniziare con esempi semplici e aumentare gradualmente il livello di difficoltà man mano che gli studenti acquisiscono sicurezza.
Utilizzare una varietà di formati di domande: Includere domande a risposta multipla, domande a risposta breve e domande a sviluppo per valutare diversi aspetti della comprensione degli studenti.
Fornire feedback regolari: Rivedere le risposte degli studenti e fornire un feedback specifico sulle aree di miglioramento.
Incoraggiare l'autovalutazione: Insegnare agli studenti come controllare il proprio lavoro e identificare gli errori comuni.

Esempi di disuguaglianze a due passaggi nel mondo reale:

Budget per un progetto: Hai un budget di €500 per un progetto scolastico e devi acquistare materiali che costano €25 ciascuno. Qual è il numero massimo di materiali che puoi acquistare?
Pianificazione di un evento: Stai organizzando una festa e hai un budget di €1000 per il cibo. Il catering costa €20 a persona. Quante persone puoi invitare?
Risparmio: Stai risparmiando per comprare una nuova bicicletta che costa €300. Hai già risparmiato €150 e guadagni €20 a settimana. Quante settimane dovrai lavorare per permetterti la bicicletta?
Consumo di carburante: La tua auto percorre 25 miglia per gallone e hai 10 galloni di benzina nel serbatoio. Qual è la distanza massima che puoi percorrere?
Tempo di studio: Hai un esame in arrivo e vuoi studiare almeno 10 ore. Hai già studiato per 2 ore. Quante ore al giorno devi studiare nei prossimi 5 giorni per raggiungere il tuo obiettivo?

Domande frequenti sulle disuguaglianze a due passaggi:

Domanda: Cosa succede quando si moltiplica o si divide entrambi i lati di una disuguaglianza per un numero negativo?
Risposta: Quando si moltiplica o si divide entrambi i lati di una disuguaglianza per un numero negativo, è necessario invertire il segno di disuguaglianza.
Domanda: Come si rappresenta graficamente la soluzione di una disuguaglianza a due passaggi su una retta numerica?
Risposta: Si utilizza un cerchio vuoto per indicare che il punto finale non è incluso nella soluzione e un cerchio pieno per indicare che il punto finale è incluso. Si utilizza quindi una freccia per indicare la direzione della soluzione.
Domanda: Qual è la differenza tra una soluzione "e" e una soluzione "o" quando si risolvono disuguaglianze?
Risposta: Una soluzione "e" significa che la soluzione deve soddisfare entrambe le disuguaglianze, mentre una soluzione "o" significa che la soluzione deve soddisfare almeno una delle due disuguaglianze.
Domanda: Ci sono casi in cui una disuguaglianza a due passaggi non ha soluzione?
Risposta: Sì, ci sono casi in cui una disuguaglianza a due passaggi non ha soluzione. Ad esempio, la disuguaglianza 2x + 5 > 2x + 10 non ha soluzione.

Consigli e trucchi per risolvere le disuguaglianze a due passaggi:

Scrivi sempre la disuguaglianza originale e segui i passaggi in modo ordinato.
Esegui le operazioni matematiche su entrambi i lati della disuguaglianza per mantenere l'equilibrio.
Ricorda di invertire il segno di disuguaglianza quando moltiplichi o dividi per un numero negativo.
Verifica sempre la tua soluzione sostituendo il valore della variabile nella disuguaglianza originale.
Fai pratica con diversi tipi di disuguaglianze a due passaggi per acquisire sicurezza.

In conclusione, padroneggiare le disuguaglianze a due passi è un passo cruciale nel vostro percorso matematico. Non solo vi fornirà gli strumenti per risolvere problemi più complessi, ma vi aiuterà anche a sviluppare capacità di pensiero critico e problem-solving applicabili a diverse situazioni della vita reale. Ricordate che la pratica è la chiave del successo: più esercitate le disuguaglianze a due passi, più vi sentirete sicuri nella vostra capacità di risolverle. Non abbiate paura di sbagliare, perché ogni errore è un'opportunità per imparare e migliorare. Continuate a esercitarvi e vedrete che le disuguaglianze a due passi diventeranno un gioco da ragazzi!