Risolvere Sistemi di Equazioni: Una Guida Completa al Metodo Grafico

11 Aug 2024
it
Emil

Immaginate un mondo in cui le relazioni complesse tra variabili si svelano davanti ai vostri occhi, trasformandosi in eleganti rappresentazioni grafiche. Benvenuti nel mondo della risoluzione di sistemi di equazioni tramite il metodo grafico, un approccio intuitivo e potente che ci permette di decifrare le interazioni tra diverse variabili e trovare soluzioni concrete a problemi apparentemente intricati.

Questo metodo affonda le sue radici nel desiderio umano di dare un volto visivo a concetti astratti. Sin dall'antichità, la rappresentazione grafica ha permesso di semplificare e rendere comprensibili dati complessi, aprendo nuove frontiere nella comprensione del mondo che ci circonda. La risoluzione grafica di sistemi di equazioni eredita questa eredità, offrendo uno strumento prezioso per affrontare una vasta gamma di sfide matematiche.

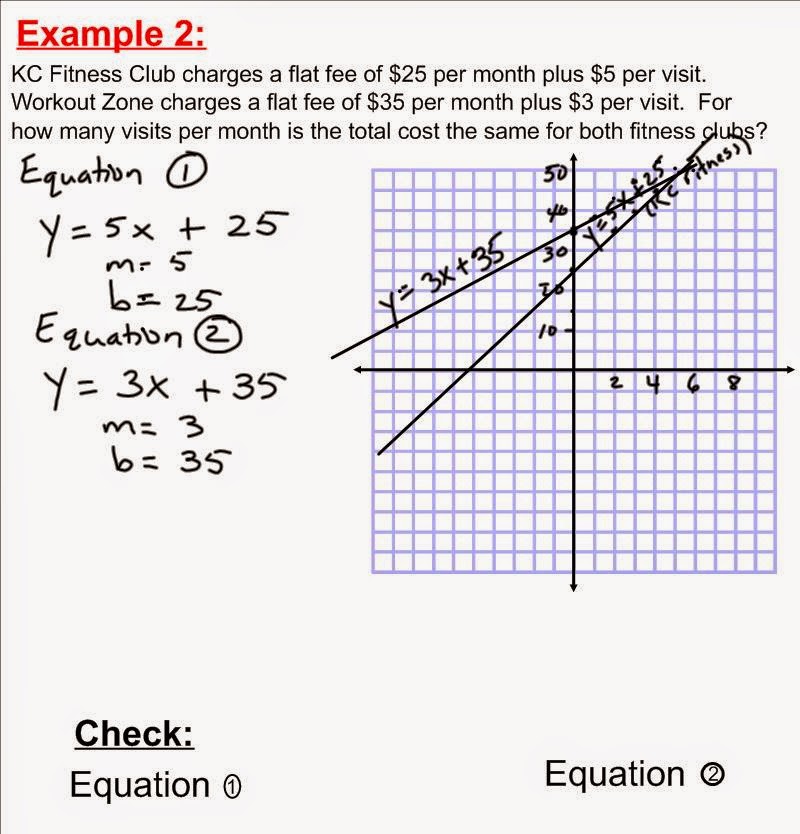
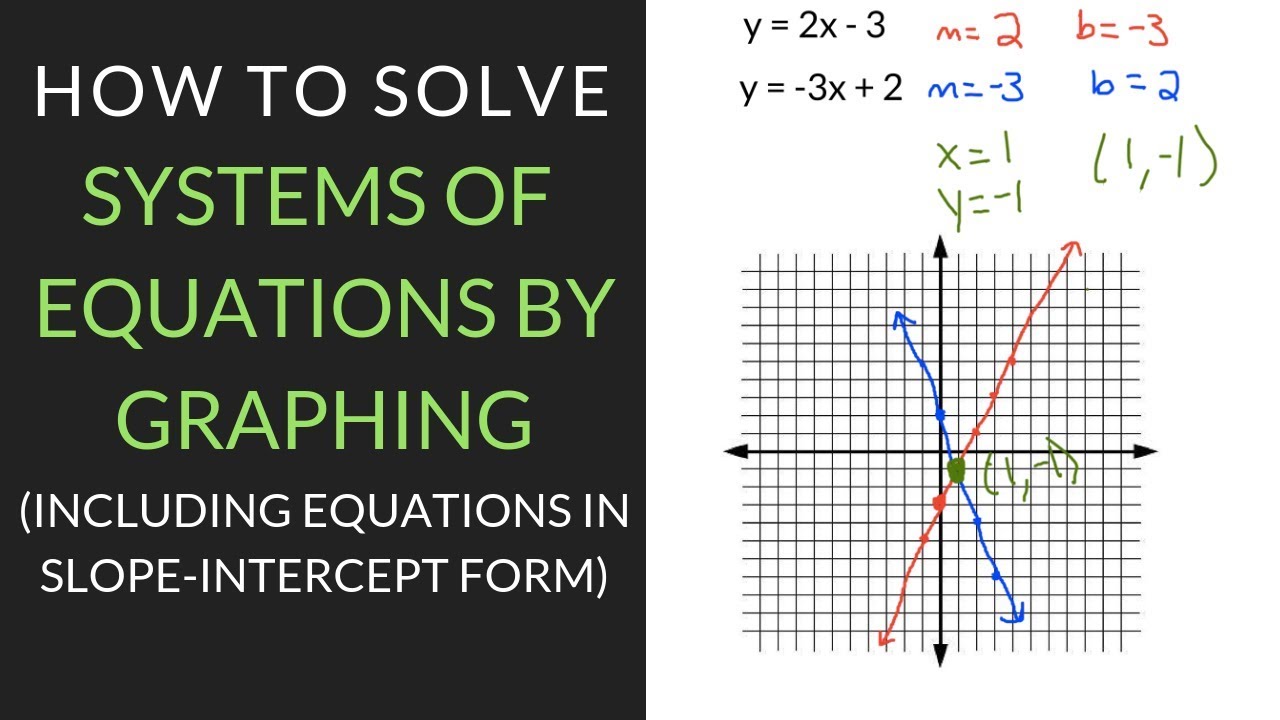
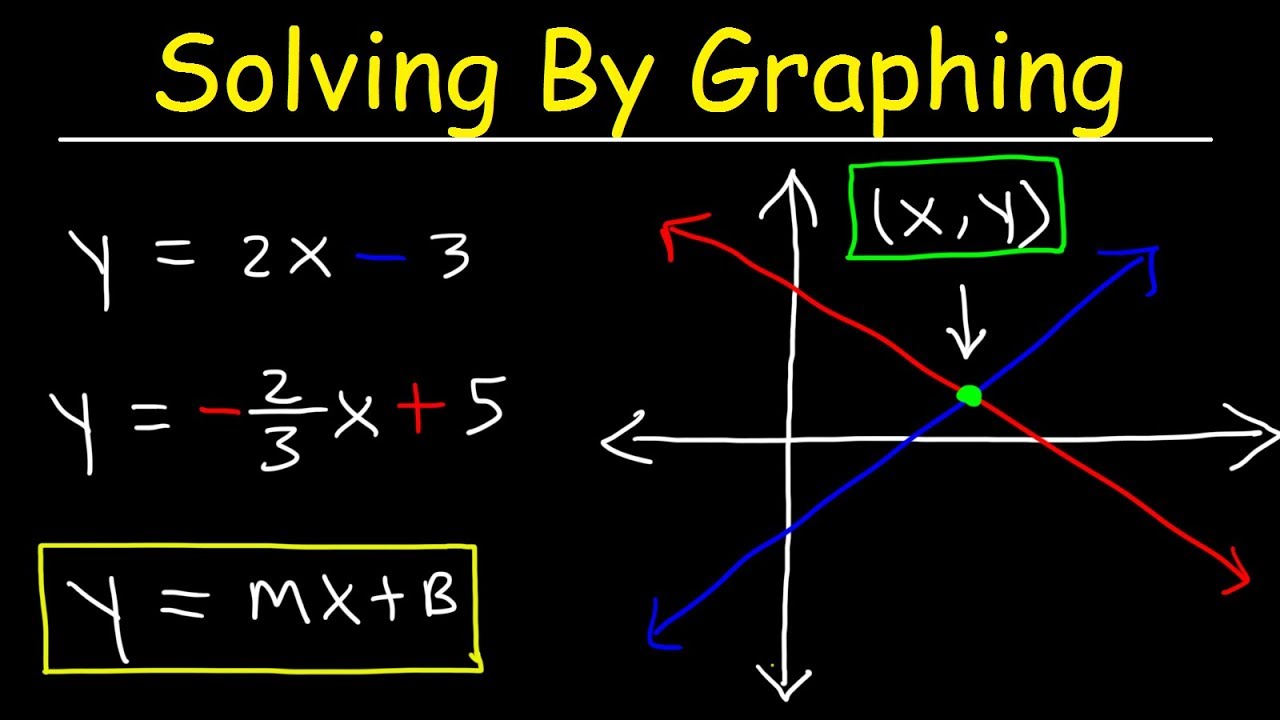
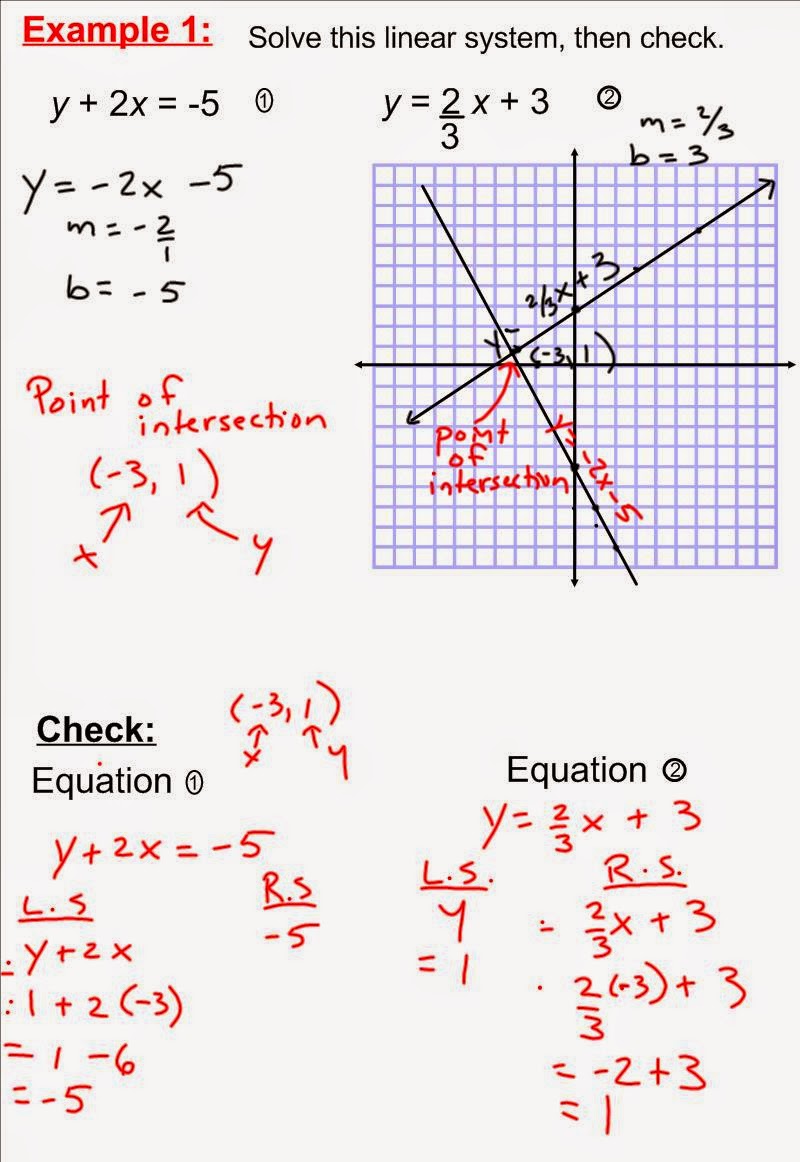
Ma cosa significa esattamente "risolvere un sistema di equazioni tramite il metodo grafico"? In termini semplici, significa rappresentare graficamente ogni equazione del sistema su uno stesso piano cartesiano. Il punto di intersezione tra le rette o le curve rappresentate corrisponde alla soluzione del sistema, ovvero all'insieme di valori che soddisfano contemporaneamente tutte le equazioni.

Questo metodo si rivela particolarmente utile in diversi contesti, ad esempio nella risoluzione di problemi di fisica, economia, ingegneria e in molte altre discipline. La sua capacità di tradurre problemi complessi in rappresentazioni visive lo rende uno strumento versatile e potente per la risoluzione di problemi in vari ambiti.

Nonostante la sua efficacia, la risoluzione grafica di sistemi di equazioni presenta alcune limitazioni. Ad esempio, la precisione della soluzione dipende dalla precisione del grafico stesso. Inoltre, il metodo può risultare meno preciso quando le soluzioni sono numeri irrazionali o quando il sistema di equazioni è particolarmente complesso. In questi casi, altri metodi di risoluzione, come la sostituzione o l'eliminazione, potrebbero rivelarsi più efficaci.

Vantaggi e Svantaggi della Risoluzione Grafica

Vantaggi	Svantaggi
Intuitivo e facile da visualizzare	Precisione limitata, soprattutto per soluzioni non intere
Utile per comprendere il comportamento delle equazioni	Difficoltà nel gestire sistemi con più di due variabili
Permette di stimare rapidamente le soluzioni	Richiede tempo per disegnare i grafici accuratamente

Sebbene non esista un metodo unico e infallibile per la risoluzione di sistemi di equazioni, il metodo grafico si distingue per la sua immediatezza e la sua capacità di rendere tangibile il legame tra algebra e geometria. Padroneggiare questo metodo significa dotarsi di uno strumento prezioso per esplorare il mondo matematico e affrontare con sicurezza le sfide che ci attendono.