Svela il Mistero: Rappresentare 'A ∩ B ∩ C' con un Diagramma di Venn

21 Jul 2024
it
Emil

2. use a venn diagram to represent: a a n b c

Avete mai osservato un gruppo di persone e notato come alcune caratteristiche si sovrappongano? Magari alcune persone amano il gelato al cioccolato, altre preferiscono la vaniglia, e alcune anime fortunate apprezzano entrambi! È qui che i diagrammi di Venn entrano in gioco, offrendo un modo elegante e chiaro per visualizzare queste intersezioni. Ma cosa succede quando le cose si fanno un po' più complesse, come quando cerchiamo di rappresentare "A ∩ B ∩ C"?

Niente panico, care menti curiose! In questo viaggio, ci addentreremo nel mondo dei diagrammi di Venn, svelando i segreti per rappresentare espressioni come "A ∩ B ∩ C" con sicurezza e chiarezza. Preparatevi a scoprire i benefici di questa potente strumento visivo, ad esplorare esempi pratici e ad apprendere consigli utili per padroneggiare l'arte dei diagrammi di Venn.

Prima di tuffarci a capofitto, rinfreschiamoci la memoria. Un diagramma di Venn utilizza cerchi (o altre forme) per illustrare le relazioni tra insiemi. Ogni cerchio rappresenta un insieme, e le aree in cui i cerchi si sovrappongono rappresentano gli elementi che gli insiemi hanno in comune. Semplice, no?

Ora, concentriamoci sulla nostra espressione chiave: "A ∩ B ∩ C". In termini matematici, "∩" rappresenta l'intersezione, ovvero gli elementi che appartengono a tutti gli insiemi coinvolti. Quindi, "A ∩ B ∩ C" si riferisce agli elementi che sono presenti in A, B e C contemporaneamente.

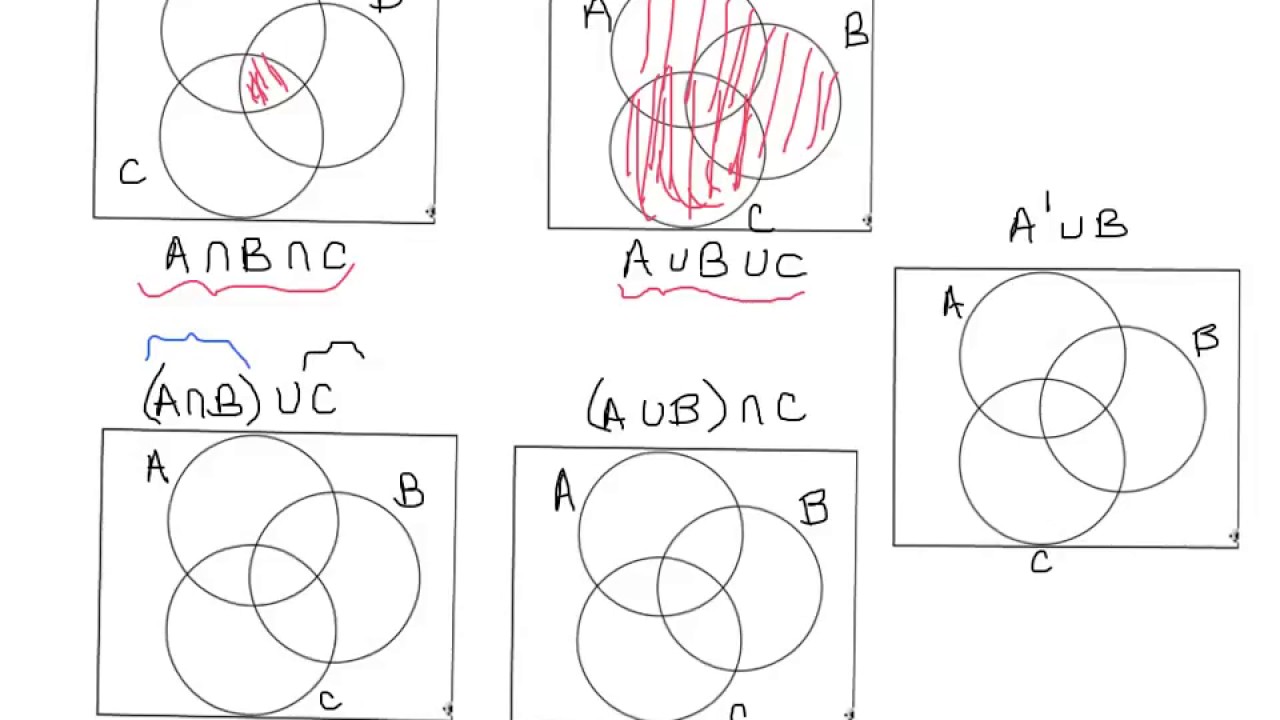
Per rappresentare "A ∩ B ∩ C" in un diagramma di Venn, disegneremmo tre cerchi che si sovrappongono, etichettati come A, B e C. L'area dove tutti e tre i cerchi si intersecano rappresenta "A ∩ B ∩ C". Questa semplice visualizzazione ci permette di comprendere rapidamente quali elementi soddisfano tutte e tre le condizioni.

Ma perché limitarci alla teoria? Immaginiamo un esempio concreto: un gruppo di studenti che praticano diversi sport. L'insieme A rappresenta gli studenti che giocano a calcio, l'insieme B quelli che praticano basket e l'insieme C quelli che si dedicano al nuoto. L'area "A ∩ B ∩ C" rappresenta i talentuosi studenti che eccellono in tutti e tre gli sport.

I diagrammi di Venn non si limitano solo alla matematica. Trovano applicazione in vari campi, come la statistica, la logica, l'informatica e persino nella vita quotidiana. La loro semplicità e versatilità li rendono uno strumento prezioso per analizzare e comunicare informazioni in modo chiaro ed efficace.

Ora che abbiamo familiarizzato con "A ∩ B ∩ C" e con i diagrammi di Venn, esploriamo alcuni dei loro benefici:

Chiarezza visiva: I diagrammi di Venn semplificano informazioni complesse, rendendole facili da comprendere a colpo d'occhio.
Identificazione di relazioni: Permettono di individuare rapidamente le relazioni tra insiemi, come intersezioni, unioni e differenze.
Risoluzione di problemi: Sono utili per risolvere problemi di logica e di insiemistica, fornendo una rappresentazione visiva delle diverse possibilità.

Padroneggiare i diagrammi di Venn è un'abilità preziosa per chiunque desideri migliorare la propria capacità di analizzare e comunicare informazioni in modo chiaro ed efficace. Con un po' di pratica, anche voi potrete utilizzare i diagrammi di Venn per svelare i misteri nascosti nei vostri dati!