Avete mai pensato a quanto la geometria influenzi la nostra vita quotidiana? Spesso, concetti matematici apparentemente astratti si celano dietro oggetti di uso comune, architetture maestose e persino fenomeni naturali. L'area laterale del cilindro, ad esempio, è un elemento chiave in innumerevoli contesti, dalla progettazione di edifici alle tubature idrauliche, fino alla creazione di contenitori per alimenti.
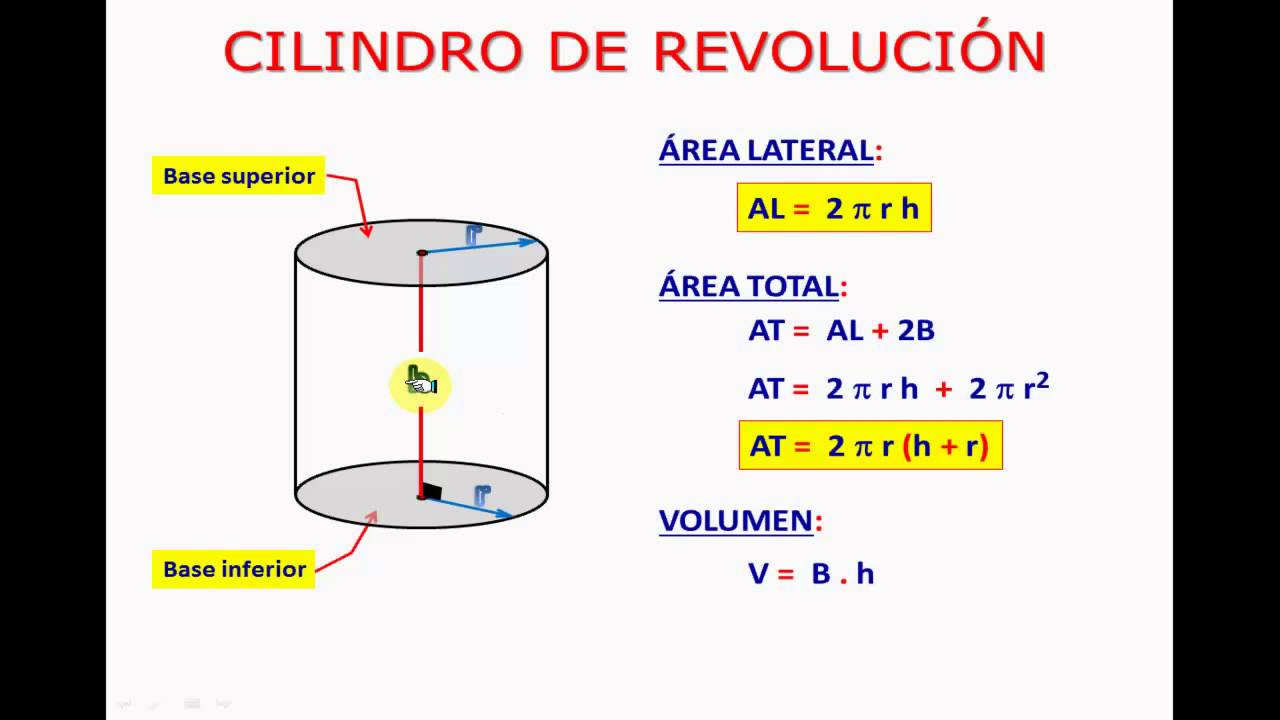
Ma cosa si intende esattamente per "area laterale del cilindro"? Immaginate un semplice barattolo di vetro: la sua superficie laterale, quella che avvolge il cerchio di base, rappresenta proprio l'area laterale del cilindro. Calcolare questa superficie è fondamentale per determinare la quantità di materiale necessaria per costruirlo, la sua capacità, e molto altro ancora.
L'importanza di questo concetto geometrico è evidente fin dall'antichità. Le colonne dei templi greci, i silos per la conservazione del grano, i rotoli di pergamena: tutti questi oggetti sfruttano le proprietà dell'area laterale del cilindro per assolvere alle loro funzioni. Pensate alla magnificenza del Partenone di Atene: la perfezione delle sue colonne, con le loro superfici laterali scandite da delicate scanalature, è un esempio tangibile di come la geometria possa fondersi con l'arte per creare capolavori senza tempo.
Oggi, l'area laterale del cilindro continua ad essere un elemento fondamentale in diversi ambiti. Nell'ingegneria civile, la progettazione di ponti, gallerie e strutture di supporto si basa sulla conoscenza approfondita di questo concetto. L'industria alimentare utilizza contenitori cilindrici per la loro resistenza e capacità di ottimizzare lo spazio, mentre in campo medico, l'area laterale del cilindro è fondamentale per la creazione di protesi, strumenti chirurgici e apparecchiature medicali.
Calcolare l'area laterale di un cilindro è relativamente semplice: basta moltiplicare la circonferenza della base per l'altezza del cilindro. Questa formula, apparentemente banale, apre le porte a una miriade di applicazioni pratiche, dimostrando come la matematica non sia solo una disciplina astratta, ma uno strumento potente per comprendere e plasmare il mondo che ci circonda.
Ad esempio, immaginiamo di dover progettare un serbatoio cilindrico per contenere 10.000 litri di acqua. Conoscendo l'altezza desiderata del serbatoio, possiamo utilizzare la formula dell'area laterale per determinare il raggio della base necessario. In questo modo, possiamo ottimizzare l'utilizzo dei materiali e garantire che il serbatoio abbia la capacità voluta.
L'area laterale del cilindro, quindi, non è solo un concetto geometrico astratto, ma un elemento tangibile che permea la nostra vita quotidiana. Dalla maestosità dei monumenti antichi alle tecnologie più innovative, la sua influenza è onnipresente, a testimonianza di come la matematica sia un linguaggio universale che ci permette di comprendere e modellare il mondo in cui viviamo.
Surface Area Formula Derivation at Bradley Martin blog - Trees By Bike
area laterale del cilindro - Trees By Bike
Como Calcular Area De Cilindro - Trees By Bike
Costruzione e Calcolo della Superficie Laterale del Cilindro - Trees By Bike
Calcular El Area Superficial De Un Cilindro - Trees By Bike
Superficie del cilindro: tutte le formule con esempi svolti - Trees By Bike
Como Calcular Area Del Cilindro - Trees By Bike
Superficie laterale e totale di un cilindro - Trees By Bike
Formula Para Calcular El Area Total De Un Cono - Trees By Bike
Calcular Area Lateral Cilindro - Trees By Bike
area laterale del cilindro - Trees By Bike
Formula De Calcular Area De Cilindro - Trees By Bike
Superficie laterale e totale di un cilindro - Trees By Bike
Calcular Area Lateral Cilindro - Trees By Bike
Mise à jour 95+ imagen formule cilindro - Trees By Bike