Immagina di essere un esploratore in un labirinto di equazioni, alla ricerca del tesoro nascosto della soluzione. Proprio come una mappa aiuta a orientarsi in un terreno sconosciuto, la risoluzione grafica dei sistemi di equazioni ci fornisce gli strumenti per visualizzare e trovare l'intersezione di due o più equazioni lineari. Questo metodo, potente e intuitivo, è come accendere una lanterna nel buio, illuminando il percorso verso la risposta corretta.
Ma come funziona esattamente questo metodo e quali sono i suoi vantaggi rispetto ad altre tecniche? In questo viaggio, esploreremo insieme i meandri della risoluzione grafica, scoprendo le sue origini storiche, i suoi punti di forza e le sue possibili insidie. Impareremo come interpretare i grafici, individuare le soluzioni e applicare questo metodo a situazioni reali. Preparati a tracciare le coordinate del successo e a svelare il potere della risoluzione grafica!
Le origini della risoluzione grafica si perdono nella notte dei tempi, intrecciate con la storia della geometria e dell'algebra. Già gli antichi Greci intuivano il potere di rappresentare equazioni su un piano cartesiano, anche se la formalizzazione del metodo avvenne secoli dopo. Matematici come René Descartes e Pierre de Fermat, nel XVII secolo, gettarono le basi della geometria analitica, permettendoci di visualizzare equazioni algebriche come forme geometriche. Da allora, la risoluzione grafica è diventata uno strumento fondamentale per studenti, scienziati e chiunque si trovi a dover affrontare sistemi di equazioni.
Ma perché questo metodo è così importante? La risposta risiede nella sua capacità di rendere tangibili concetti astratti. Mentre la risoluzione algebrica può sembrare un'arida manipolazione di simboli, la risoluzione grafica ci permette di "vedere" le equazioni come rette su un grafico. Il punto di intersezione tra queste rette rappresenta la soluzione del sistema, ovvero l'unico punto che soddisfa entrambe le equazioni. In altre parole, la risoluzione grafica trasforma un problema algebrico in un'intuitiva ricerca visiva.
Naturalmente, anche la risoluzione grafica presenta alcune sfide. Ad esempio, la precisione del grafico è fondamentale per ottenere una soluzione accurata. Un piccolo errore nel tracciare le rette può portare a un punto di intersezione errato. Inoltre, la risoluzione grafica può essere meno efficiente della risoluzione algebrica, soprattutto quando si ha a che fare con sistemi di equazioni con molte variabili o coefficienti complessi. Nonostante queste limitazioni, la risoluzione grafica rimane uno strumento potente per comprendere e risolvere sistemi di equazioni, soprattutto per chi muove i primi passi nel mondo dell'algebra.
Per illustrare meglio il concetto, prendiamo un semplice esempio: immagina di dover organizzare un viaggio e di voler confrontare i costi di due compagnie di autonoleggio. La prima compagnia offre un noleggio fisso di €30 più €0.50 al chilometro, mentre la seconda compagnia propone un noleggio fisso di €20 più €0.70 al chilometro. Rappresentando queste offerte come equazioni su un grafico, possiamo facilmente individuare il punto di intersezione, ovvero il numero di chilometri per cui il costo di entrambe le compagnie è identico. Questa informazione ci aiuterà a scegliere l'opzione più conveniente in base alle nostre esigenze.
In definitiva, la risoluzione grafica dei sistemi di equazioni è un viaggio affascinante che ci permette di esplorare il mondo dell'algebra da una prospettiva innovativa. Nonostante le sue sfide, la sua capacità di rendere visibili concetti astratti la rende uno strumento prezioso per studenti, insegnanti e chiunque desideri svelare i misteri delle equazioni lineari. Come un faro che illumina la notte, la risoluzione grafica ci guida verso la soluzione, aiutandoci a prendere decisioni consapevoli e a navigare con sicurezza nel mare dell'algebra.
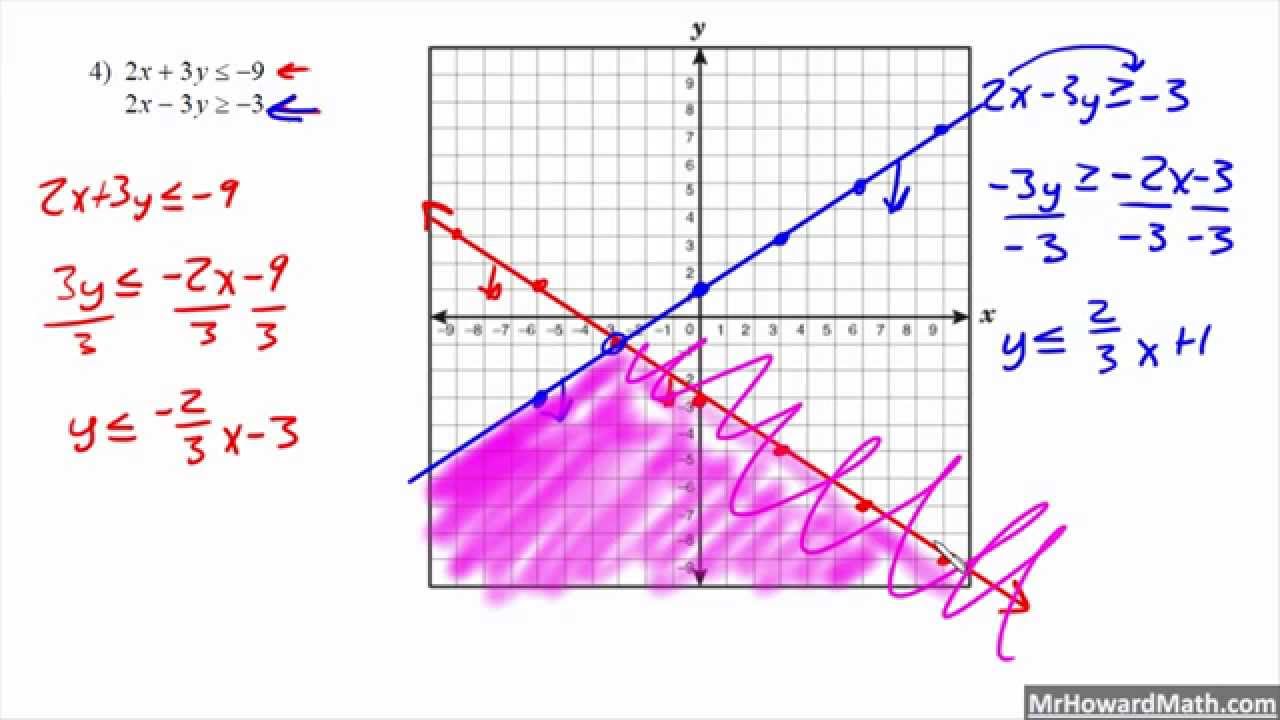
Graphing Quadratic And Linear Systems Solver - Trees By Bike
Solving Systems Of Linear Equations Worksheet - Trees By Bike
Systems Of Inequalities Quiz Part 1 - Trees By Bike
Worksheet System Of Equation By Graphing - Trees By Bike
System Of Inequalities How To Solve - Trees By Bike
Systems Of Linear Inequalities Practice - Trees By Bike
System Of Linear Inequalities Pdf - Trees By Bike
Solving Systems Of Equations By Graphing Worksheets Answer K - Trees By Bike
Solving Systems By Graphing Worksheet - Trees By Bike
Graphing Systems Of Equations Worksheet - Trees By Bike
Solving Systems Of Linear Equations By Graphing Worksheets - Trees By Bike
Solving A System Of Equations Worksheet - Trees By Bike
Graphing Systems Of Linear Equations Worksheets - Trees By Bike