Immaginate di dover incartare un regalo cilindrico: come calcolare la quantità di carta necessaria senza sprechi? O di dover dipingere la superficie esterna di un silos? La risposta risiede nella comprensione di un concetto geometrico fondamentale: l'area laterale del cilindro. Questo articolo vi guiderà alla scoperta della formula, vi mostrerà come applicarla e vi fornirà gli strumenti per risolvere problemi pratici.
L'area laterale di un cilindro rappresenta la superficie che si estende tra le due basi circolari. Pensate ad un rotolo di carta da cucina: la parte che possiamo toccare lateralmente, senza considerare le basi, costituisce l'area laterale. La sua importanza si manifesta in molteplici contesti, dalla progettazione architettonica alla produzione industriale, fino ai calcoli domestici più semplici.
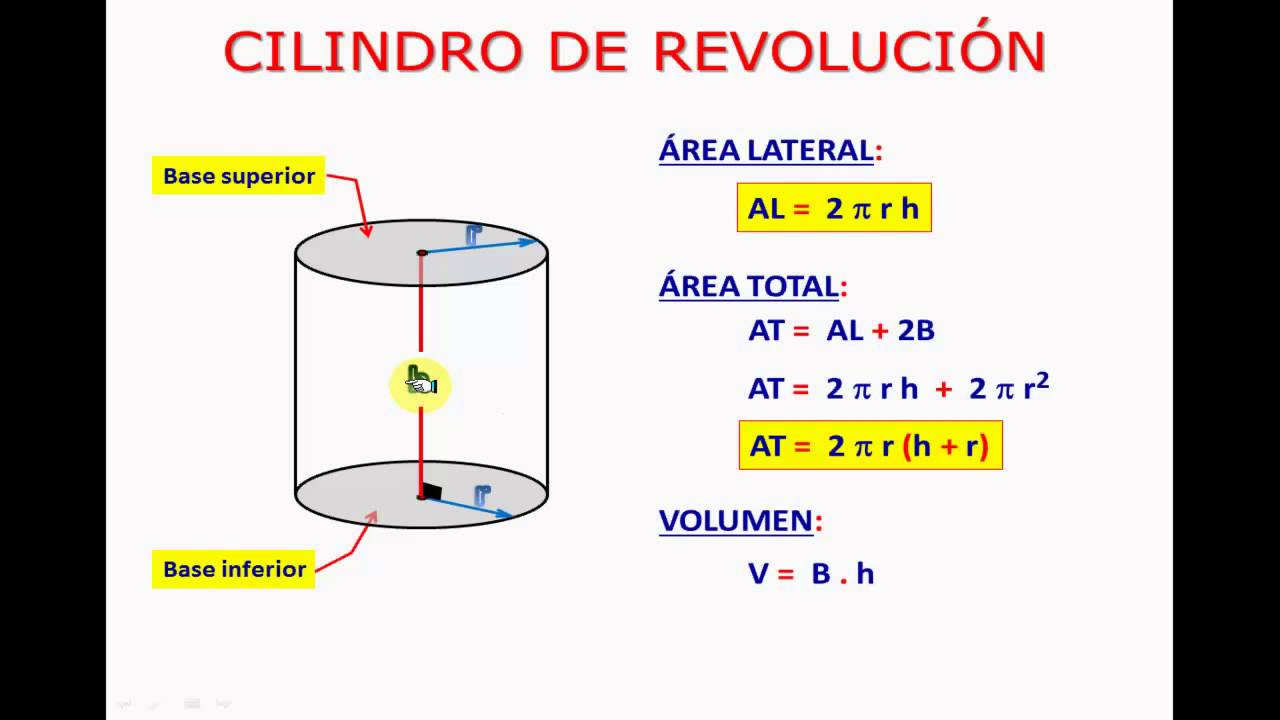
La formula per calcolare l'area laterale di un cilindro è sorprendentemente semplice: 2πrh, dove "r" rappresenta il raggio della base circolare e "h" l'altezza del cilindro. La sua origine risale agli albori della geometria, con contributi da parte di civiltà antiche come quella greca e babilonese. La comprensione di questa formula ha permesso di realizzare opere architettoniche imponenti e di sviluppare tecnologie innovative nel corso dei secoli.
Tuttavia, la semplicità della formula non deve trarre in inganno. Spesso, la difficoltà risiede nell'individuare correttamente i dati necessari, soprattutto quando si ha a che fare con problemi reali. Un errore comune è confondere il diametro con il raggio, oppure non considerare l'unità di misura, portando a risultati errati.
Per applicare la formula correttamente, è fondamentale seguire alcuni passaggi chiave: innanzitutto, identificare il raggio (r) e l'altezza (h) del cilindro. Assicurarsi che le unità di misura siano coerenti (ad esempio, entrambi in centimetri o metri). Successivamente, moltiplicare il raggio per 2π (circa 6,28) e infine moltiplicare il risultato per l'altezza. Il valore ottenuto rappresenterà l'area laterale del cilindro, espressa nell'unità di misura al quadrato.
Vantaggi e Svantaggi
Come per ogni concetto matematico, l'apprendimento della formula per l'area laterale del cilindro presenta vantaggi e svantaggi:
| Vantaggi | Svantaggi |
|---|---|
| Calcolo preciso dell'area laterale | Applicabilità limitata a forme cilindriche perfette |
| Utilità in diversi campi, dalla scienza all'ingegneria | Difficoltà nel calcolo per forme irregolari o complesse |
| Formula semplice da ricordare e applicare | Rischio di errori se i dati non sono inseriti correttamente |
Nonostante le sue limitazioni, la formula per l'area laterale del cilindro rimane uno strumento fondamentale per comprendere e risolvere problemi geometrici. La sua padronanza apre le porte ad un mondo di applicazioni pratiche e stimola la mente a pensare in modo critico e creativo.
In conclusione, l'area laterale del cilindro è un concetto matematico essenziale con una vasta gamma di applicazioni. La sua formula semplice, 2πrh, può essere applicata per risolvere problemi reali e comprendere meglio il mondo che ci circonda. Con la pratica e la conoscenza, chiunque può padroneggiare questo concetto e utilizzarlo per i propri scopi.
Calculo Da Area Lateral Do Cilindro - Trees By Bike
Prismas e Cilindros no Enem - Trees By Bike
Calcular El Area Lateral De Un Cilindro - Trees By Bike
Formula De Calcular Area De Cilindro - Trees By Bike
Calcular Area Lateral De Um Cilindro - Trees By Bike
Calcular El Area Superficial De Un Cilindro - Trees By Bike
area laterale cilindro formula - Trees By Bike
Richtig Kritisch Schatten cilindro area lateral irregulär Innereien Lamm - Trees By Bike
Calcular Area Lateral Cilindro - Trees By Bike
Calcular Área del Cilindro - Trees By Bike
Superficie laterale e totale di un cilindro, terza media - Trees By Bike
Formula Para Calcular A Area Da Base De Um Cilindro - Trees By Bike
Area Superficie Laterale Cilindro - Trees By Bike
Calcular Área del Cilindro - Trees By Bike
Formula de area del cilindro - Trees By Bike