Pernahkah anda terfikir bagaimana sistem nombor yang kita gunakan hari ini terbentuk? Bagaimana kita boleh mengira objek, mengukur masa, atau bahkan memprogram komputer tanpa nombor? Jawapannya terletak pada konsep asas yang dikenali sebagai bilangan bulat.
Dalam pengembaraan matematik ini, kita akan menyelami dunia menakjubkan "bilangan bulat bermula dari." Bersiap sedia untuk meneroka asal usulnya, kepentingan dalam pelbagai bidang, dan bagaimana ia membentuk pemahaman kita tentang dunia di sekeliling kita.
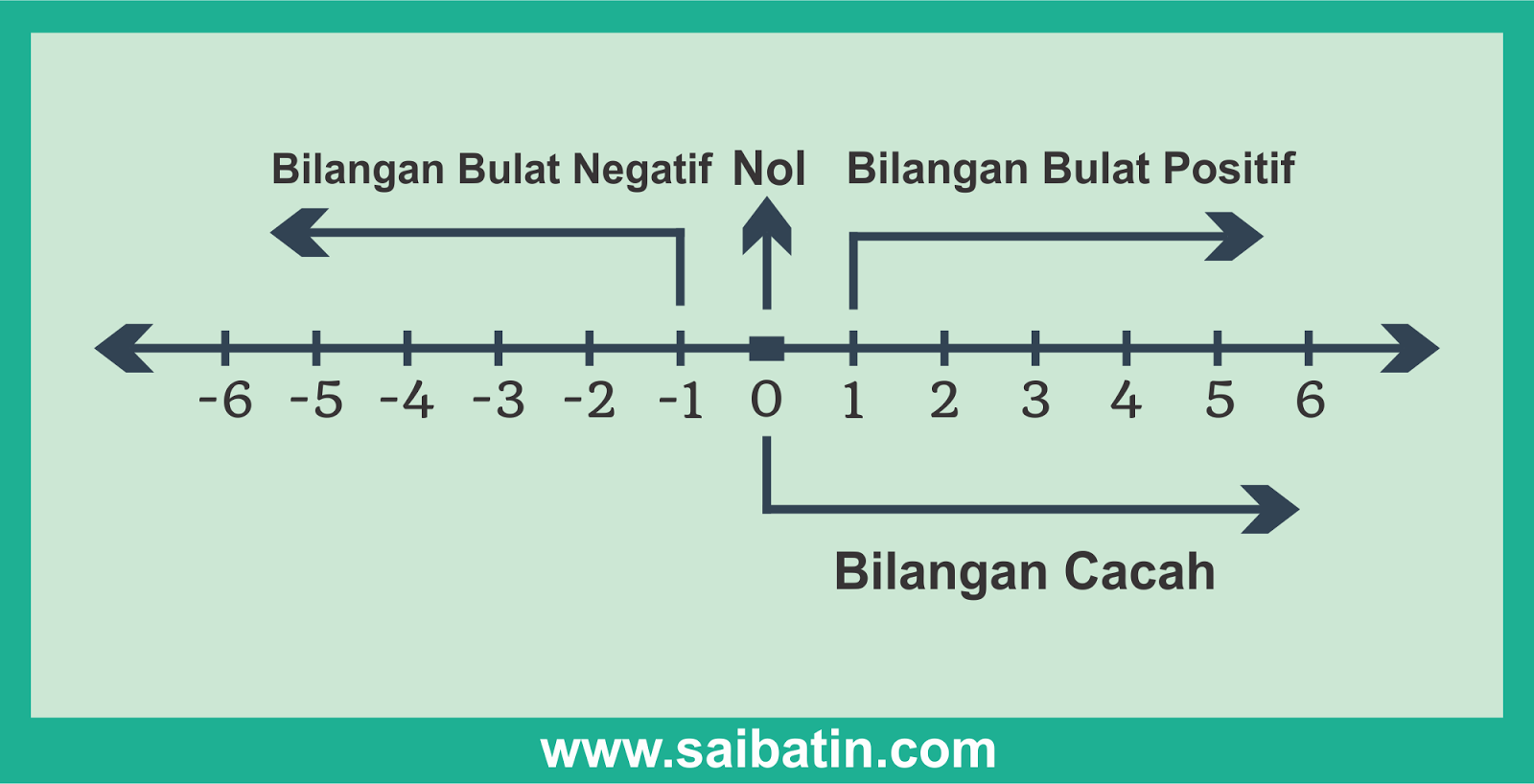
Bayangkan sebuah garisan nombor yang terbentang tanpa batas di kedua-dua arah. Di tengah-tengahnya terletak angka sifar (0), titik permulaan kita. Dari sini, kita boleh bergerak ke kanan, menemui nombor positif seperti 1, 2, 3, dan seterusnya, yang mewakili kuantiti yang semakin meningkat. Sebaliknya, bergerak ke kiri membawa kita ke alam nombor negatif seperti -1, -2, -3, dan seterusnya, menunjukkan kuantiti yang kurang daripada sifar.
Gabungan nombor positif, sifar, dan nombor negatif membentuk set "bilangan bulat." Konsep "bermula dari" merujuk kepada titik rujukan, yang dalam konteks ini biasanya ialah sifar. Kita boleh memulakan kiraan dari sifar dan bergerak ke arah positif atau negatif bergantung kepada keperluan kita.
Pemahaman tentang bilangan bulat bermula dari adalah penting dalam pelbagai aspek kehidupan. Daripada transaksi kewangan dan pengiraan saintifik hingga pengaturcaraan komputer dan analisis data, bilangan bulat membentuk asas kepada operasi matematik yang tidak terkira banyaknya.
Kelebihan dan Kekurangan Bilangan Bulat Bermula Dari
| Kelebihan | Kekurangan |
|---|---|
| Memudahkan pengiraan dan perbandingan nombor. | Tidak dapat mewakili nilai pecahan atau perpuluhan secara tepat. |
| Membentuk asas kepada sistem nombor dan operasi matematik yang lebih kompleks. | Penggunaan dalam konteks tertentu mungkin memerlukan penukaran kepada jenis data lain. |
Amalan Terbaik untuk Melaksanakan Bilangan Bulat Bermula Dari
- Fahami konteks: Tentukan sama ada penggunaan bilangan bulat sesuai untuk situasi tertentu.
- Pilih jenis data yang betul: Bahasa pengaturcaraan menawarkan pelbagai jenis data untuk mewakili bilangan bulat, pilih yang paling sesuai berdasarkan julat nilai yang diperlukan.
- Periksa ralat limpahan: Pastikan operasi matematik tidak melebihi had jenis data yang digunakan.
- Gunakan pengaturcaraan modular: Bahagikan kod kepada fungsi atau modul yang lebih kecil untuk meningkatkan kebolehbacaan dan kebolehgunaan semula.
- Uji dengan teliti: Pastikan kod berfungsi seperti yang diharapkan dengan pelbagai input dan keadaan.
Contoh Nyata Bilangan Bulat Bermula Dari
- Suhu: Suhu boleh dinyatakan dalam darjah Celsius atau Fahrenheit, dengan nilai positif dan negatif yang mewakili suhu di atas dan di bawah takat beku.
- Ketinggian: Ketinggian diukur berbanding aras laut, dengan nilai positif menunjukkan ketinggian di atas aras laut dan nilai negatif menunjukkan kedalaman di bawah aras laut.
- Baki Akaun Bank: Baki akaun bank boleh positif (kredit) atau negatif (debit).
- Koordinat Geografi: Garisan longitud dan latitud menggunakan bilangan bulat untuk menentukan lokasi di Bumi.
- Masa: Kita menggunakan bilangan bulat untuk mewakili tahun, bulan, hari, jam, minit, dan saat.
Soalan Lazim
1. Apakah perbezaan antara bilangan bulat dan nombor bulat?
Bilangan bulat merangkumi nombor bulat positif, sifar, dan nombor bulat negatif. Nombor bulat hanya merujuk kepada nombor bulat positif dan sifar.
2. Apakah aplikasi bilangan bulat dalam sains komputer?
Bilangan bulat digunakan secara meluas dalam sains komputer untuk penyimpanan data, pengalamatan memori, indeks array, dan banyak lagi.
3. Apakah had penggunaan bilangan bulat?
Bilangan bulat mempunyai had atas dan bawah bergantung kepada jenis data yang digunakan. Operasi yang melebihi had ini boleh menyebabkan ralat limpahan.
4. Bagaimanakah bilangan bulat digunakan dalam kriptografi?
Bilangan bulat memainkan peranan penting dalam algoritma kriptografi untuk tujuan penyulitan dan penyahsulitan data.
5. Apakah peranan bilangan bulat dalam pembangunan permainan?
Bilangan bulat digunakan untuk mewakili kedudukan objek, skor pemain, tahap kesihatan, dan pelbagai parameter lain dalam permainan video.
6. Bagaimana cara menukar nombor perpuluhan kepada bilangan bulat?
Fungsi pembulatan seperti "round", "ceil", dan "floor" boleh digunakan untuk menukar nombor perpuluhan kepada bilangan bulat terdekat.
7. Apakah kepentingan bilangan bulat dalam kecerdasan buatan?
Bilangan bulat digunakan dalam algoritma pembelajaran mesin untuk memproses dan menganalisis data, dan membuat ramalan.
8. Bagaimana cara mempelajari lebih lanjut tentang bilangan bulat dan aplikasinya?
Terdapat banyak sumber dalam talian dan buku teks matematik yang menyediakan maklumat mendalam tentang bilangan bulat dan kepentingannya.
Kesimpulan
Bilangan bulat bermula dari adalah konsep asas namun sangat penting yang membentuk asas kepada matematik dan pelbagai disiplin ilmu lain. Memahami sifat, operasi, dan aplikasi bilangan bulat adalah penting untuk menyelesaikan masalah, membuat keputusan yang tepat, dan menghargai kerumitan dunia di sekeliling kita. Dengan menguasai konsep ini, kita membuka jalan untuk penerokaan dan penemuan yang lebih mendalam dalam bidang masing-masing.
Bilangan Bulat Beserta Contoh Soalnya - Trees By Bike
bilangan bulat dimulai dari - Trees By Bike
Algoritma, Flowchart dan Contoh Pemrograman Untuk Menghitung Faktorial - Trees By Bike
Bilangan Cacah, Bulat, Dan Asli Beserta Contohnya - Trees By Bike
bilangan bulat dimulai dari - Trees By Bike
Pengertian Bilangan Cacah dan Bilangan Asli Lengkap dengan Contohnya - Trees By Bike
bilangan bulat dimulai dari - Trees By Bike
Penjumlahan dan Pengurangan Bilangan Bulat - Trees By Bike
bilangan bulat dimulai dari - Trees By Bike
Download soal bahasa inggris kelas 2 semester 1 dan kunci jawaban doc - Trees By Bike
Foto : Cara Menentukan Nilai Kelipatan 4 yang Lebih dari 7 - Trees By Bike
Cara Mudah Menghitung Bilangan Bulat Berpangkat Positif Dan Negatif - Trees By Bike
Gambarlah Garis Bilangan Bulat yang Kurang Dari 5 dan Lebih Dari - Trees By Bike
Bilangan Bulat Yang Diurutkan Dari Terkecil Adalah - Trees By Bike
Contoh Soal Sistem Bilangan Real Kalkulus Roboguru Mobile Legends - Trees By Bike