Pernahkah anda memerhatikan bentuk geometri yang selalu hadir di sekeliling kita? Salah satu yang paling mudah dan sering kita temui ialah segitiga. Tiga sisi, tiga sudut, tetapi tahukah anda rahsia di sebalik mengira sisi-sisinya?
Menguasai ilmu mengira sisi segitiga bukan sahaja penting untuk menyelesaikan masalah matematik di sekolah, malah ia membuka pintu kepada pemahaman lebih mendalam tentang dunia di sekeliling kita. Daripada seni bina bangunan megah hinggalah rekaan fesyen yang anggun, segitiga memainkan peranan penting dalam pelbagai bidang.
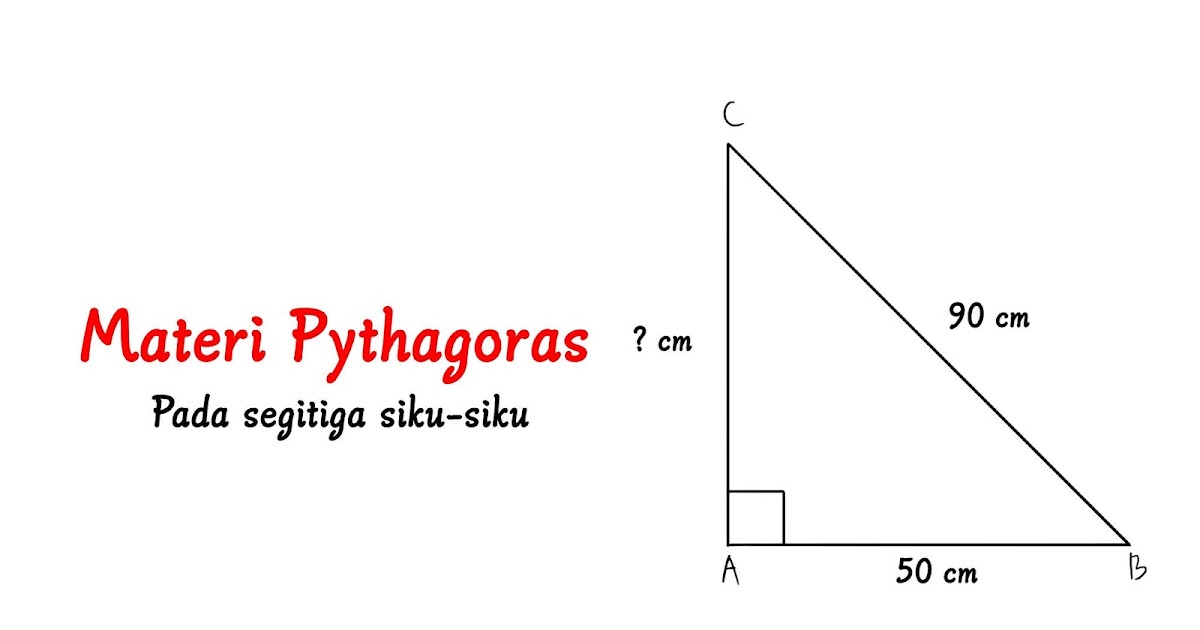
Sejak zaman dahulu lagi, ahli matematik telah mengkaji dan merumuskan pelbagai cara untuk mengira sisi segitiga. Teorem Pythagoras, contohnya, merupakan salah satu formula paling terkenal yang digunakan secara meluas hingga ke hari ini.
Namun, cabaran utama bagi sesetengah orang adalah memahami konsep dan formula yang pelbagai ini. Ada yang keliru dengan jenis-jenis segitiga, manakala yang lain pula sukar untuk mengaplikasikan rumus dengan betul.
Oleh itu, artikel ini akan membimbing anda langkah demi langkah untuk menguasai teknik mengira sisi segitiga dengan mudah dan menyeronokkan. Kami akan meneroka pelbagai kaedah, contoh praktikal, serta tip berguna yang boleh diaplikasikan dalam kehidupan seharian anda.
Kelebihan dan Kekurangan Mempelajari Cara Mengira Sisi Segitiga
| Kelebihan | Kekurangan |
|---|---|
| Meningkatkan kemahiran matematik dan penyelesaian masalah | Memahami konsep geometri boleh menjadi sukar bagi sesetengah individu |
| Berguna dalam pelbagai bidang seperti seni bina, kejuruteraan, dan reka bentuk | Memerlukan hafalan dan pemahaman pelbagai rumus |
| Membantu memahami konsep geometri yang lebih kompleks | - |
5 Amalan Terbaik untuk Menguasai Pengiraan Sisi Segitiga
Berikut adalah 5 amalan terbaik untuk membantu anda menguasai pengiraan sisi segitiga:
- Fahami Jenis-jenis Segitiga: Kenal pasti jenis segitiga (sama sisi, sama kaki, atau tak sama kaki) kerana setiap jenis mempunyai ciri unik yang mempengaruhi pengiraan.
- Kuasai Teorem Pythagoras: Hafal dan fahami aplikasi Teorem Pythagoras (a² + b² = c²) untuk mencari sisi miring (hipotenus) dalam segitiga bersudut tepat.
- Latih Tubi dengan Contoh Soalan: Kerjakan pelbagai contoh soalan yang melibatkan pengiraan sisi segitiga untuk mengukuhkan pemahaman dan meningkatkan kemahiran anda.
- Gunakan Alat Bantu Visual: Lukis gambar rajah segitiga untuk membantu menggambarkan masalah dan memudahkan proses pengiraan.
- Jangan Takut untuk Meminta Bantuan: Jika anda menghadapi kesukaran, jangan teragak-agak untuk bertanya kepada guru, rakan, atau mencari sumber pembelajaran tambahan.
Kesimpulan
Menguasai cara mengira sisi segitiga adalah kemahiran berharga yang boleh diaplikasikan dalam pelbagai aspek kehidupan. Dengan memahami konsep asas, menguasai formula penting, dan rajin berlatih, anda boleh dengan mudah menyelesaikan masalah geometri yang melibatkan segitiga. Teruskan usaha dan jangan mudah berputus asa, kerana setiap usaha pasti membuahkan hasil yang membanggakan. Selamat mencuba!
Rumus Trigonometri: Ulasan dan Berbagai Macam Contoh Soalnya - Trees By Bike
Rumus Sin, Cos, Tan Dan Tabel - Trees By Bike
Cara Menghitung Sisi Segitiga Siku Siku - Trees By Bike
Cara Menghitung Sisi Miring Segitiga - Trees By Bike
Cara Mencari Sudut Segitiga, Lengkap Rumus dan Contohnya - Trees By Bike
Rumus Luas Segitiga Cara Menghitung Hingga C - Trees By Bike
Cara Menghitung Sisi Segitiga - Trees By Bike
Cara Menghitung Luas Segitiga dan Keliling Segitiga - Trees By Bike
Cara menghitung sisi miring segitiga 2021 - Trees By Bike
Rumus Luas Segitiga Sama Sisi Tanpa Tinggi - Trees By Bike
Cara Menghitung Sisi Miring Segitiga - Trees By Bike
Mencari Nilai Jarak Pada Hukum Coulomb - Trees By Bike
Cara Mencari Tinggi Segitiga - Trees By Bike
Cara Menghitung Volume Limas Segitiga Alas Segitiga Sama Kaki Siku Siku - Trees By Bike
Cara Mudah Menghitung Panjang Sisi Pada Segitiga Siku Siku Sama Kaki - Trees By Bike