Pernahkah anda berhadapan dengan persamaan matematik yang kelihatan rumit dan membuat anda terfikir, "Bagaimana cara menyelesaikannya?" Jangan risau, anda tidak keseorangan! Dalam dunia matematik yang luas, terdapat satu teknik yang boleh membantu anda menyelesaikan persamaan kuadratik dengan lebih mudah dan pantas, iaitu pemfaktoran kuasa dua sempurna.
Bayangkan anda seorang detektif yang cuba menyelesaikan satu teka-teki. Pemfaktoran kuasa dua sempurna adalah seperti kunci utama yang boleh membuka pintu kepada penyelesaian. Dengan memahami konsep ini, anda akan dapat menyelesaikan persamaan kuadratik dengan lebih yakin dan efisien.
Tapi, apa sebenarnya pemfaktoran kuasa dua sempurna ini? Mengapa ia begitu penting dalam matematik, terutamanya dalam menyelesaikan persamaan kuadratik? Mari kita terokai bersama rahsia di sebalik teknik ini dan bagaimana ia boleh membantu anda menguasai persamaan kuadratik dengan mudah.
Secara ringkasnya, pemfaktoran kuasa dua sempurna adalah proses mengubah satu ungkapan matematik kepada bentuk yang lebih ringkas dan mudah difahami. Teknik ini melibatkan mencari dua nombor yang apabila di darab menghasilkan nombor ketiga, dan apabila di tambah menghasilkan nombor kedua.
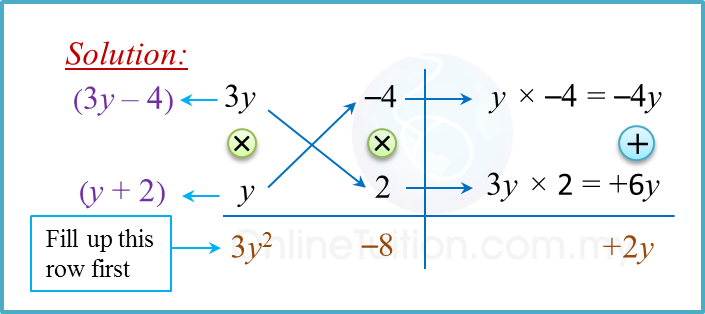
Contohnya, ungkapan x² + 6x + 9 boleh difaktorkan kepada (x + 3)². Ini kerana (x + 3) × (x + 3) = x² + 6x + 9. Dengan memahami konsep ini, anda akan dapat menyelesaikan persamaan kuadratik dengan lebih mudah dan pantas.
Kelebihan dan Kekurangan Pemfaktoran Kuasa Dua Sempurna
Seperti teknik matematik yang lain, pemfaktoran kuasa dua sempurna juga mempunyai kelebihan dan kekurangannya tersendiri. Mari kita lihat dengan lebih lanjut:
| Kelebihan | Kekurangan |
|---|---|
| Memudahkan penyelesaian persamaan kuadratik. | Hanya boleh digunakan pada persamaan kuadratik tertentu. |
| Membantu memahami konsep algebra dengan lebih baik. | Memerlukan latihan dan pemahaman konsep yang kukuh. |
| Berguna dalam pelbagai bidang seperti fizik, kejuruteraan, dan ekonomi. | Boleh menjadi rumit jika melibatkan nombor pecahan atau nombor perpuluhan. |
Amalan Terbaik untuk Melaksanakan Pemfaktoran Kuasa Dua Sempurna
Berikut adalah beberapa amalan terbaik untuk membantu anda menguasai teknik pemfaktoran kuasa dua sempurna:
- Kuasai konsep asas algebra. Pastikan anda memahami konsep seperti pemboleh ubah, pemalar, dan operasi asas matematik.
- Latih tubi dengan contoh yang mudah. Mulakan dengan contoh yang mudah dan tingkatkan kesukarannya secara beransur-ansur.
- Gunakan kaedah yang sesuai. Terdapat pelbagai kaedah untuk melakukan pemfaktoran kuasa dua sempurna. Pilih kaedah yang paling mudah dan sesuai untuk anda.
- Semak jawapan anda. Selepas menyelesaikan persamaan, semak jawapan anda dengan menggantikan nilai yang anda perolehi ke dalam persamaan asal.
- Bersabar dan jangan mudah putus asa. Menguasai teknik ini memerlukan masa dan latihan. Jangan mudah putus asa jika anda menghadapi kesukaran pada awalnya.
Kesimpulan
Pemfaktoran kuasa dua sempurna adalah teknik yang sangat berguna dalam menyelesaikan persamaan kuadratik. Walaupun kelihatan rumit pada mulanya, dengan pemahaman yang baik tentang konsep asas dan latihan yang konsisten, anda pasti boleh menguasai teknik ini dengan mudah. Ingatlah untuk sentiasa berlatih dan jangan mudah putus asa. Teruskan usaha dan anda akan dapat menyelesaikan persamaan kuadratik dengan lebih yakin dan cekap. Selamat mencuba!
pemfaktoran kuasa dua sempurna - Trees By Bike
2.2 Factorisation of Quadratic Expression - Trees By Bike
pemfaktoran kuasa dua sempurna - Trees By Bike
pemfaktoran kuasa dua sempurna - Trees By Bike
Solved: Senaraikan semua kuasa dua sempurna di antara 50 dan 120. List - Trees By Bike
Download 2.2 Pemfaktoran (Part 3 : Kaedah Beza Dua Sebutan Kuasa Dua - Trees By Bike
: Dengan menggunakan kaedah pemfaktoran perdana, tentukan sama ada 215 - Trees By Bike
Menyelesaikan Persamaan Kuadratik Menggunakan Kaedah Pemfaktoran Rumus - Trees By Bike
PEMFAKTORAN: KUASA DUA SEMPURNA - Trees By Bike
Solved: 12. (a) Dengan menggunakan kaedah pemfaktoran perdana - Trees By Bike
pemfaktoran kuasa dua sempurna - Trees By Bike
c Dengan menggunakan kaedah pemfaktoran perdana, tentukan sama ada 215 - Trees By Bike
Nombor Kuasa Dua Sempurna Senarai Nombor Kuasa Dua Sempurna Start - Trees By Bike
Dengan menggunakan kaedah pemfaktoran perdana, ten - Trees By Bike
pemfaktoran kuasa dua sempurna - Trees By Bike