Pernahkah anda terserempak dengan simbol "!" dalam persamaan matematik dan tertanya-tanya apa maksudnya? Jangan risau, anda tidak keseorangan! Simbol ini, yang dikenali sebagai "tanda seru," memainkan peranan yang unik dan penting dalam dunia matematik. Ia mewakili operasi matematik yang dipanggil "faktorial." Dalam artikel ini, kita akan menyelami dunia faktorial, meneroka definisi, sejarah, aplikasi, dan kepentingannya dalam pelbagai bidang matematik.
Secara ringkasnya, faktorial sesuatu nombor bulat positif, yang diwakili oleh simbol "!", ialah hasil darab semua nombor bulat positif yang sama atau kurang daripada nombor tersebut. Sebagai contoh, 5! (dibaca sebagai "lima faktorial") bersamaan dengan 5 * 4 * 3 * 2 * 1, menghasilkan 120.
Sejarah faktorial boleh dikesan kembali ke zaman India purba, dengan rujukan ditemui dalam teks Jain seawal abad ke-3 SM. Konsep ini kemudiannya dikembangkan oleh ahli matematik India dan Arab sebelum diperkenalkan ke Eropah pada Zaman Pertengahan. Notasi tanda seru (!) untuk faktorial mula digunakan secara meluas pada abad ke-19, memberikan kemudahan dan kejelasan dalam menulis ungkapan matematik.
Faktorial memainkan peranan penting dalam pelbagai bidang matematik, termasuk kombinatorik, kebarangkalian, dan kalkulus. Dalam kombinatorik, faktorial digunakan untuk mengira bilangan cara untuk menyusun objek atau memilih subset objek daripada satu set. Contohnya, jika anda mempunyai 5 kad berbeza, terdapat 5! (atau 120) cara berbeza untuk menyusunnya.
Dalam kebarangkalian, faktorial digunakan untuk mengira kebarangkalian peristiwa tertentu berlaku. Contohnya, jika anda memilih secara rawak 3 bola daripada beg yang mengandungi 5 bola (2 merah dan 3 biru), kebarangkalian memilih 2 bola merah dan 1 bola biru boleh dikira menggunakan faktorial.
Faktorial juga penting dalam kalkulus, terutamanya dalam bidang siri tak terhingga dan fungsi khas. Banyak fungsi penting, seperti fungsi gamma dan fungsi Bessel, boleh ditakrifkan dan dimanipulasi menggunakan faktorial.
Walaupun faktorial mungkin kelihatan seperti konsep matematik yang mudah, ia mempunyai aplikasi yang luas dan mendalam dalam pelbagai bidang. Memahami faktorial membuka pintu kepada pemahaman yang lebih mendalam tentang konsep matematik dan aplikasinya dalam dunia nyata. Daripada mengira kebarangkalian kepada menyelesaikan masalah kejuruteraan yang kompleks, faktorial memainkan peranan penting dalam memajukan pengetahuan dan teknologi kita.
Kelebihan dan Kekurangan Tanda Seru dalam Matematik
| Kelebihan | Kekurangan |
|---|---|
| Memudahkan penulisan ungkapan matematik yang melibatkan pendaraban berulang. | Boleh mengelirukan jika tidak biasa dengan notasi tersebut. |
| Digunakan secara meluas dalam pelbagai bidang matematik, seperti kombinatorik dan kebarangkalian. | Pengiraan faktorial boleh menjadi sangat besar dengan cepat apabila nombor input meningkat. |
| Mempunyai aplikasi praktikal dalam sains komputer, fizik, dan kejuruteraan. | Tidak ditakrifkan untuk nombor negatif atau nombor bukan bulat. |
Lima Amalan Terbaik untuk Melaksanakan Tanda Seru dalam Matematik
- Pastikan anda memahami definisi dan sifat faktorial sebelum menggunakannya dalam pengiraan.
- Berhati-hati dengan turutan operasi dan gunakan tanda kurung dengan betul apabila menggabungkan faktorial dengan operasi matematik lain.
- Permudahkan ungkapan faktorial dengan membatalkan faktor sepunya apabila mungkin.
- Gunakan kalkulator atau perisian matematik untuk mengira faktorial untuk nombor besar.
- Semak semula jawapan anda untuk memastikan ia munasabah dalam konteks masalah.
Lima Contoh Nyata Berkaitan dengan Tanda Seru dalam Matematik
- Mengira bilangan cara untuk menyusun sekumpulan orang dalam barisan.
- Menentukan kebarangkalian untuk memenangi loteri.
- Mengira bilangan cara untuk memilih pasukan daripada sekumpulan pemain.
- Menghitung bilangan laluan yang mungkin dalam graf.
- Menyelesaikan masalah pengoptimuman dalam algoritma komputer.
Lima Cabaran dan Penyelesaian Berkaitan dengan Tanda Seru dalam Matematik
- Cabaran: Mengendalikan faktorial untuk nombor yang sangat besar. Penyelesaian: Gunakan penghampiran seperti formula Stirling atau perisian komputer yang direka untuk mengendalikan nombor besar.
- Cabaran: Menentukan faktorial untuk nombor bukan bulat. Penyelesaian: Gunakan fungsi gamma, yang merupakan generalisasi faktorial kepada nombor kompleks.
- Cabaran: Memudahkan ungkapan yang melibatkan faktorial. Penyelesaian: Gunakan sifat faktorial, seperti n! = n(n-1)!, dan batalkan faktor sepunya.
- Cabaran: Memahami kepentingan faktorial dalam konteks aplikasi dunia nyata. Penyelesaian: Kaji contoh dan masalah yang menunjukkan bagaimana faktorial digunakan dalam bidang seperti kebarangkalian, statistik, dan fizik.
- Cabaran: Mengajar konsep faktorial kepada pelajar dengan cara yang menarik dan mudah difahami. Penyelesaian: Gunakan alat bantu visual, contoh konkrit, dan aktiviti langsung untuk menggambarkan konsep faktorial.
Soalan Lazim tentang Tanda Seru dalam Matematik
- Apakah maksud tanda seru dalam matematik?
- Tanda seru dalam matematik mewakili operasi faktorial.
- Bagaimana anda mengira faktorial sesuatu nombor?
- Faktorial sesuatu nombor bulat positif ialah hasil darab semua nombor bulat positif dari 1 hingga nombor tersebut. Contohnya, 5! = 5 * 4 * 3 * 2 * 1 = 120.
- Apakah beberapa aplikasi faktorial dalam matematik?
- Faktorial digunakan dalam pelbagai bidang matematik, termasuk kombinatorik, kebarangkalian, statistik, dan kalkulus.
- Bolehkah anda mengira faktorial untuk nombor negatif?
- Tidak, faktorial hanya ditakrifkan untuk nombor bulat positif.
- Apakah faktorial sifar?
- Faktorial sifar ialah 1 (0! = 1).
- Apakah beberapa sifat faktorial?
- Beberapa sifat penting faktorial termasuk n! = n(n-1)!, 0! = 1, dan (n+1)! = (n+1)n!.
- Bagaimana faktorial digunakan dalam kehidupan seharian?
- Faktorial digunakan dalam pelbagai aplikasi kehidupan seharian, seperti mengira kebarangkalian, menyusun objek, dan menyelesaikan masalah pengoptimuman.
- Apakah beberapa sumber untuk mempelajari lebih lanjut tentang faktorial?
- Anda boleh menemui maklumat lanjut tentang faktorial dalam buku teks matematik, laman web matematik, dan ensiklopedia dalam talian.
Tips dan Trik Berkaitan dengan Tanda Seru dalam Matematik
- Ingat bahawa faktorial nombor besar boleh menjadi sangat besar. Gunakan kalkulator atau perisian matematik untuk memudahkan pengiraan.
- Perhatikan sifat faktorial, seperti n! = n(n-1)!, untuk memudahkan ungkapan dan menyelesaikan masalah dengan lebih cekap.
- Kaji contoh dan aplikasi dunia nyata untuk memahami kepentingan dan kaitan faktorial dalam pelbagai bidang.
Kesimpulannya, tanda seru dalam matematik, yang mewakili operasi faktorial, merupakan konsep penting dengan aplikasi yang luas. Daripada mengira kebarangkalian kepada menyelesaikan masalah kejuruteraan yang kompleks, pemahaman tentang faktorial adalah penting untuk sesiapa sahaja yang ingin mempelajari dunia matematik dan aplikasinya. Dengan menguasai definisi, sifat, dan aplikasi faktorial, anda akan bersedia untuk menghadapi cabaran matematik yang lebih kompleks dan membuka kunci pemahaman yang lebih mendalam tentang alam semesta. Terokai keajaiban faktorial dan kembangkan ufuk matematik anda hari ini!
Tanda Lebih Besar Dan Lebih Kecil Dalam Matematika - Trees By Bike
Ícone de erro sinaliza ícone Ponto de exclamação dentro de um ícone de - Trees By Bike
Tanda Seru Dalam Matematika - Trees By Bike
tanda seru dalam matematika disebut - Trees By Bike
Punto de exclamación, símbolo de exclamación iconos de computadora - Trees By Bike
Tanda Sama Dengan Dalam Matematika - Trees By Bike
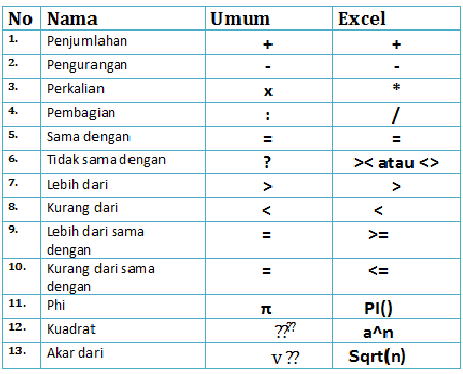
Simbol Simbol Matematika Lengkap - Trees By Bike
tanda seru dalam matematika disebut - Trees By Bike
tanda seru dalam matematika disebut - Trees By Bike
Arti Tanda Dalam Matematika - Trees By Bike
Arti Tanda Dalam Matematika - Trees By Bike