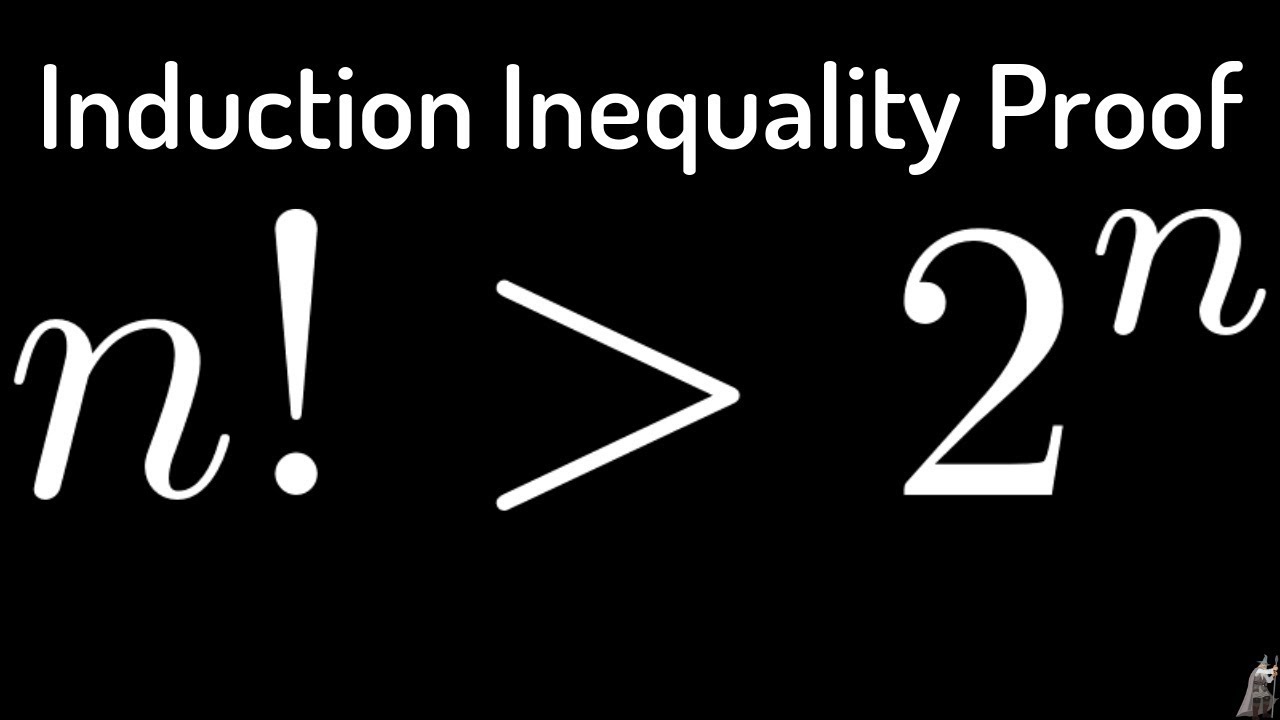De wereld van de wiskunde draait om bewijzen. Het is de manier waarop we de waarheid van wiskundige uitspraken vaststellen, van eenvoudige vergelijkingen tot complexe theorema's. Maar hoe bewijs je nu eigenlijk een wiskundige stelling? Deze vraag is de kern van dit artikel, waarin we de kunst van het bewijzen verkennen.
Het bewijzen van een stelling is als het bouwen van een stevige brug. Elke stap moet logisch volgen op de vorige, en het eindresultaat moet een solide constructie zijn die de tand des tijds kan doorstaan. Het proces vereist precisie, creativiteit en een diepgaand begrip van de onderliggende principes.
Er bestaan verschillende bewijsmethoden, elk met zijn eigen sterke punten en toepassingen. Van inductie tot tegenspraak, elke methode biedt een unieke aanpak om de waarheid van een stelling aan te tonen. Het kiezen van de juiste methode is cruciaal voor het succesvol bewijzen van een stelling.
De zoektocht naar een bewijs kan een uitdagende, maar ook zeer lonende ervaring zijn. Het vereist een combinatie van logisch redeneren, intuïtie en doorzettingsvermogen. Maar de voldoening van het vinden van een elegant en overtuigend bewijs is ongeëvenaard.
In dit artikel duiken we dieper in de wereld van wiskundige bewijzen. We verkennen verschillende bewijsmethoden, bespreken veelvoorkomende valkuilen en bieden praktische tips voor het succesvol bewijzen van stellingen. Of je nu een student bent die worstelt met bewijzen of een ervaren wiskundige die zijn kennis wil opfrissen, dit artikel biedt waardevolle inzichten in de kunst van het bewijzen.
De geschiedenis van wiskundige bewijzen gaat terug tot de oude Grieken, met figuren als Euclides die de basis legden voor de deductieve methode. Het belang van bewijzen ligt in het vaststellen van de absolute waarheid van wiskundige uitspraken, wat essentieel is voor de ontwikkeling van de wiskunde als wetenschap.
Een eenvoudig voorbeeld van een bewijs is het bewijzen dat de som van twee even getallen altijd even is. Stel dat de twee even getallen 2n en 2m zijn, waarbij n en m gehele getallen zijn. De som is dan 2n + 2m = 2(n + m), wat weer een even getal is, omdat het deelbaar is door 2.
Helaas is "n n n" te abstract om concrete voorbeelden, voor- en nadelen, of een checklist te geven. De term is te vaag om specifieke bewijsmethoden of toepassingen te bespreken. Het is belangrijk om concrete wiskundige stellingen te hebben om mee te werken.
Veelgestelde vragen:
1. Wat is een wiskundig bewijs? Een wiskundig bewijs is een logische redenering die de waarheid van een wiskundige stelling aantoont.
2. Welke bewijsmethoden zijn er? Er zijn verschillende bewijsmethoden, waaronder inductie, tegenspraak, directe bewijzen en bewijzen uit het ongerijmde.
3. Waarom zijn wiskundige bewijzen belangrijk? Wiskundige bewijzen zijn essentieel voor het vaststellen van de waarheid van wiskundige uitspraken.
4. Hoe begin ik met het bewijzen van een stelling? Begin met het begrijpen van de stelling en de onderliggende concepten.
5. Wat zijn veelvoorkomende fouten bij het bewijzen? Veelvoorkomende fouten zijn onder meer onvolledige redeneringen en het gebruik van onjuiste aannames.
6. Hoe kan ik mijn bewijsvaardigheden verbeteren? Oefening baart kunst! Probeer zoveel mogelijk stellingen te bewijzen.
7. Zijn er hulpmiddelen beschikbaar voor het bewijzen? Ja, er zijn boeken en online bronnen beschikbaar.
8. Wat als ik vastloop tijdens het bewijzen? Raadpleeg een docent of mede-student voor hulp.
Tips en trucs: Begin met eenvoudige bewijzen en werk geleidelijk aan naar complexere stellingen. Bestudeer voorbeelden van bewijzen en probeer de gebruikte technieken te begrijpen.
Conclusie: Het bewijzen van wiskundige stellingen is een essentieel onderdeel van de wiskunde. Het vereist logisch redeneren, creativiteit en doorzettingsvermogen. Door verschillende bewijsmethoden te beheersen en veel te oefenen, kun je je bewijsvaardigheden verbeteren en de fascinerende wereld van de wiskunde verder verkennen. Het begrijpen en toepassen van bewijsmethoden is cruciaal voor iedereen die zich bezighoudt met wiskunde, van studenten tot professionals. De zoektocht naar een elegant en overtuigend bewijs kan uitdagend zijn, maar de voldoening van het vinden van de oplossing is ongeëvenaard. Blijf oefenen, blijf leren en ontdek de schoonheid en kracht van wiskundige bewijzen.
how to prove n n n - Trees By Bike
how to prove n n n - Trees By Bike
how to prove n n n - Trees By Bike
how to prove n n n - Trees By Bike
Solved 3 nn25 is divisible by 6 for each integer n - Trees By Bike
how to prove n n n - Trees By Bike
+2.jpg)
how to prove n n n - Trees By Bike
Solved 20 points Use mathematical induction to prove n nn - Trees By Bike
Prove that for any positive integer n n3 n is always divisible by 6 - Trees By Bike
Solved Use induction to prove n nn 1n 2 Xii1 3 - Trees By Bike
Solved Prove n n3 for all n6 Here is the start of my - Trees By Bike
3Prove the following by using the principle of mathematical induction - Trees By Bike
how to prove n n n - Trees By Bike
how to prove n n n - Trees By Bike
Solved Use a combinatorial argument to prove n n n nn - Trees By Bike