Stel je voor: je bent een architect die een wolkenkrabber ontwerpt. Hoe zorg je ervoor dat de muren op de juiste hoek staan en het gebouw stabiel is? Of misschien ben je een gameontwikkelaar die realistische bewegingen voor personages wil creëren. Hoe vertaal je die bewegingen naar wiskundige formules? Het antwoord ligt in de wondere wereld van trigonometrie, met de onmisbare functies cosinus, sinus en tangens.
Cosinus, sinus en tangens, vaak afgekort als cos, sin en tan, zijn de hoekstenen van de trigonometrie, een tak van de wiskunde die zich bezighoudt met de relaties tussen hoeken en zijden van driehoeken. Deze functies stellen ons in staat om onbekende zijden of hoeken van een rechthoekige driehoek te berekenen, zolang we de waarde van één hoek (anders dan de rechte hoek) en de lengte van één zijde kennen.
De geschiedenis van deze trigonometrische functies gaat terug tot de oude beschavingen van Griekenland, Egypte en India, waar ze werden gebruikt voor astronomie, navigatie en landmeting. Astronomen gebruikten ze om de positie van sterren te bepalen, terwijl zeevaarders ze gebruikten om te navigeren op open zee. Vandaag de dag zijn cosinus, sinus en tangens niet meer weg te denken uit verschillende vakgebieden, waaronder natuurkunde, engineering, computergraphics en muziek.
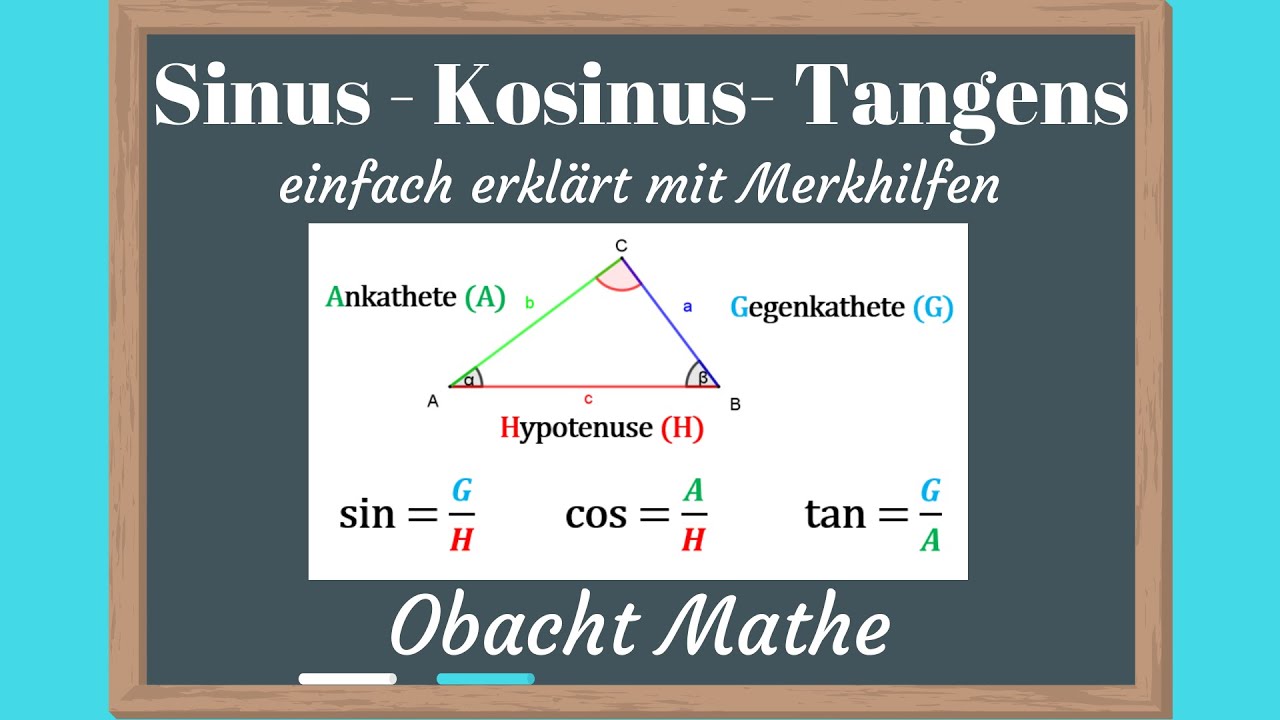
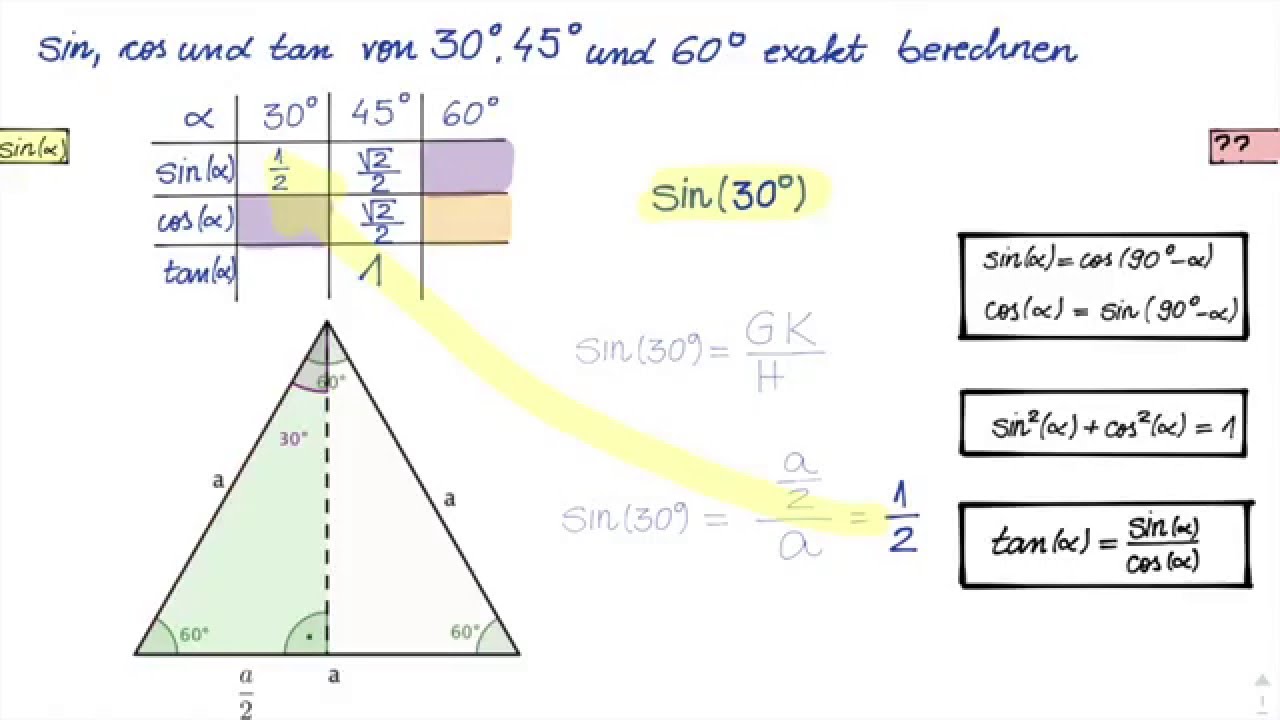
Maar hoe werken cosinus, sinus en tangens nu precies? Laten we een rechthoekige driehoek bekijken. De sinus van een hoek is gelijk aan de overstaande zijde gedeeld door de schuine zijde. De cosinus van een hoek is gelijk aan de aanliggende zijde gedeeld door de schuine zijde. En de tangens van een hoek is gelijk aan de overstaande zijde gedeeld door de aanliggende zijde. Deze verhoudingen, bekend als de 'SOH CAH TOA'-regel, vormen de basis voor het oplossen van trigonometrische problemen.
Cosinus, sinus en tangens zijn krachtige instrumenten die ons helpen de wereld om ons heen te begrijpen en te manipuleren. Of het nu gaat om het bouwen van bruggen, het voorspellen van de baan van een komeet of het creëren van adembenemende visuele effecten in films, deze trigonometrische functies spelen een cruciale rol.
Hoewel cosinus, sinus en tangens ongelooflijk nuttig zijn, is het belangrijk te onthouden dat hun nauwkeurigheid afhangt van de nauwkeurigheid van de gebruikte gegevens. Kleine meetfouten kunnen leiden tot grote discrepanties in de berekeningen, vooral bij het werken met grote afstanden of hoeken. Daarom is het essentieel om nauwkeurige metingen te gebruiken en de resultaten te verifiëren.
Kortom, cosinus, sinus en tangens zijn onmisbare hulpmiddelen in de wiskunde en vele andere wetenschappen. Hun vermogen om de relaties tussen hoeken en zijden van driehoeken te beschrijven, heeft geleid tot talloze ontdekkingen en innovaties door de geschiedenis heen. Terwijl we blijven zoeken naar kennis en de grenzen van ons begrip verleggen, zullen cosinus, sinus en tangens ongetwijfeld een centrale rol blijven spelen in onze reis.
cos sin und tan - Trees By Bike
cos sin und tan - Trees By Bike
cos sin und tan - Trees By Bike
cos sin und tan - Trees By Bike
cos sin und tan - Trees By Bike
cos sin und tan - Trees By Bike
cos sin und tan - Trees By Bike
cos sin und tan - Trees By Bike
cos sin und tan - Trees By Bike
cos sin und tan - Trees By Bike
cos sin und tan - Trees By Bike
cos sin und tan - Trees By Bike
cos sin und tan - Trees By Bike
cos sin und tan - Trees By Bike
cos sin und tan - Trees By Bike