Stel je voor: je bent bezig met een DIY-project en je moet de hoogte van een rechthoekig stuk hout berekenen. Of misschien ben je aan het bakken en wil je weten hoe hoog je bakvorm is. Hoe pak je dat aan? Het berekenen van de hoogte van een rechthoek is een essentiële wiskundige vaardigheid die in veel situaties van pas komt. In dit artikel duiken we in de wereld van rechthoeken en ontdekken we de verschillende manieren om hun hoogte te bepalen.
De hoogte van een rechthoek vinden is eigenlijk best wel simpel als je de juiste informatie hebt. We hebben het hier over basis geometrie, maar het is verrassend hoe vaak deze kennis van pas komt in het dagelijks leven. Denk aan het inrichten van je kamer, het plannen van een tuin, of zelfs het maken van een kunstwerk.
Om de hoogte te berekenen, heb je de oppervlakte en de breedte van de rechthoek nodig. De formule is simpel: hoogte = oppervlakte / breedte. Het is eigenlijk een soort puzzel waarbij je twee stukjes hebt (oppervlakte en breedte) en het derde stukje (hoogte) moet vinden.
Maar wat als je de oppervlakte niet hebt? Geen paniek! Er zijn andere manieren om de hoogte te berekenen. Als je bijvoorbeeld de diagonaal en de breedte kent, kun je de stelling van Pythagoras gebruiken. Het klinkt misschien ingewikkeld, maar het is eigenlijk best wel cool.
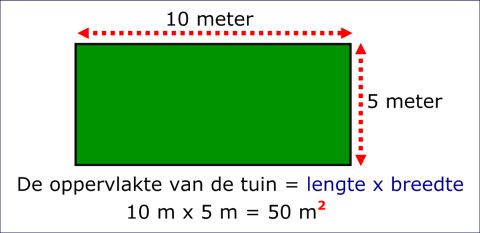
Laten we eens een praktisch voorbeeld bekijken. Stel je voor dat je een rechthoekige tuin hebt met een oppervlakte van 20 vierkante meter en een breedte van 4 meter. Om de hoogte te berekenen, deel je de oppervlakte (20) door de breedte (4). Het resultaat is 5 meter. Dus, de hoogte van je tuin is 5 meter. Makkelijk, toch?
De oorsprong van de geometrie, en dus ook het concept van de rechthoek en zijn eigenschappen, gaat terug tot de oude beschavingen. Egypte en Babylonië gebruikten meetkunde voor praktische doeleinden zoals landmeting en bouwwerken. De Grieken ontwikkelden de geometrie verder tot een formele wetenschap.
Een belangrijk probleem bij het berekenen van de hoogte is dat je de juiste gegevens nodig hebt. Zonder de oppervlakte of de breedte (of andere relevante informatie) kun je de hoogte niet berekenen. Het is dus cruciaal om de juiste metingen te verrichten.
Voorbeeld: Een rechthoek heeft een oppervlakte van 30 cm² en een breedte van 5 cm. De hoogte is dan 30 cm² / 5 cm = 6 cm.
Voordelen van het kennen van deze berekening:
1. Praktisch in het dagelijks leven: Van klussen tot het inpakken van cadeaus, het komt overal van pas.
2. Begrip van wiskundige concepten: Het helpt je om geometrie beter te begrijpen.
3. Probleemoplossende vaardigheden: Het traint je analytische denkvermogen.
Stap-voor-stap handleiding:
1. Bepaal de oppervlakte en de breedte van de rechthoek.
2. Deel de oppervlakte door de breedte.
3. Het resultaat is de hoogte van de rechthoek.
Voor- en nadelen
| Voordeel | Nadeel |
|---|---|
| Eenvoudige berekening | Vereist accurate metingen |
Beste praktijken:
1. Gebruik altijd de juiste eenheden.
2. Controleer je berekeningen.
3. Gebruik een rekenmachine voor nauwkeurigheid.
4. Maak een schets van de rechthoek.
5. Zorg voor nauwkeurige metingen.
Veelgestelde vragen:
1. Wat is de formule voor de hoogte van een rechthoek? Hoogte = oppervlakte / breedte.
2. Wat heb ik nodig om de hoogte te berekenen? De oppervlakte en de breedte.
3. Kan ik de hoogte berekenen zonder de oppervlakte? Ja, met de diagonaal en breedte via de stelling van Pythagoras.
4. Wat zijn de eenheden voor hoogte? Dezelfde eenheden als de breedte (cm, m, etc.).
5. Waar kan ik meer informatie vinden over rechthoeken? Online wiskunde websites en leerboeken.
6. Hoe controleer ik mijn berekening? Vermenigvuldig de berekende hoogte met de breedte; het resultaat moet de oppervlakte zijn.
7. Wat als ik de diagonaal ken? Je kunt de stelling van Pythagoras gebruiken.
8. Wat is de stelling van Pythagoras in relatie tot een rechthoek? a² + b² = c², waarbij a en b de zijden en c de diagonaal is.
Tips en trucs: Maak altijd een schets! Visualisatie helpt enorm bij het begrijpen van het probleem. Gebruik een liniaal voor nauwkeurige metingen. Oefening baart kunst, dus probeer verschillende voorbeelden.
Het berekenen van de hoogte van een rechthoek is een fundamentele vaardigheid die in diverse situaties van pas komt. Van alledaagse klusjes tot complexe wiskundige problemen, het begrijpen van deze eenvoudige formule opent deuren naar een beter begrip van geometrie en probleemoplossing. Door de stappen te volgen en de tips te onthouden, kun je met gemak de hoogte van elke rechthoek berekenen. Dus, de volgende keer dat je voor deze uitdaging staat, weet je precies wat je moet doen! Vergeet niet: oefening baart kunst, dus blijf oefenen en je zult een expert worden in het berekenen van de hoogte van een rechthoek. Dit is een vaardigheid die je je hele leven lang zult gebruiken, dus neem de tijd om het goed te leren. Het is een investering die zich zeker zal terugbetalen.
hoe bereken je de hoogte van een rechthoek - Trees By Bike
hoe bereken je de hoogte van een rechthoek - Trees By Bike
Transitievergoeding wanneer heeft de werknemer er recht op en hoe - Trees By Bike
Hoe Bereken Je De Oppervlakte Van Een Driehoek Simpele Uitleg En Formule - Trees By Bike
hoe bereken je de hoogte van een rechthoek - Trees By Bike
Hoe Bereken Je Gemiddeld Uit - Trees By Bike
Inhoudsmaten omrekenen van kubieke naar liters - Trees By Bike
Hoe Bereken Ik M2 Een Eenvoudige Gids - Trees By Bike
hoe bereken je de hoogte van een rechthoek - Trees By Bike
Bereken de hoogte van een piramide - Trees By Bike
Hoe Bereken Je De Oppervlakte Van Een Driehoek - Trees By Bike
hoe bereken je de hoogte van een rechthoek - Trees By Bike
Hoe Bereken Ik Een Vierkante Meter - Trees By Bike
Hoe bereken je een driehoek - Trees By Bike
Hoe bereken je de hoogte van een kegel als de hoek bekend is - Trees By Bike