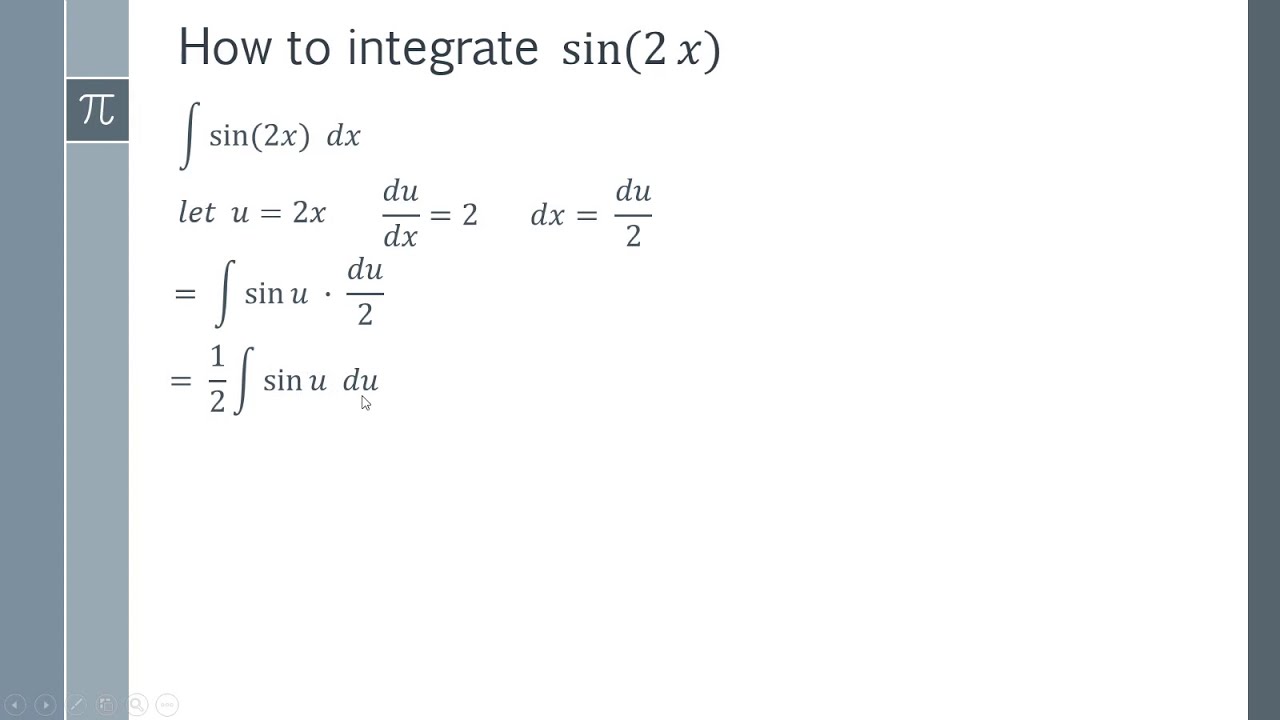De wereld van de wiskunde zit vol met elegante concepten en krachtige tools die ons helpen de complexiteit van de wereld om ons heen te begrijpen. Eén zo'n concept is integratie, een fundamenteel onderdeel van de calculus dat ons in staat stelt om oppervlaktes, volumes en veranderingssnelheden te berekenen. Binnen de wereld van de integratie is de integraal van sin²(x) dx een fascinerend geval met unieke eigenschappen en toepassingen.
Maar wat maakt deze integraal zo bijzonder? In tegenstelling tot de ogenschijnlijk eenvoudige integraal van sin(x) dx, die direct leidt tot -cos(x) + C, vereist de integraal van sin²(x) dx een iets meer doordachte aanpak. Het vereist een vleugje trigonometrische identiteit en een greep uit de gereedschapskist van integratietechnieken om een elegante oplossing te vinden.
De integraal van sin²(x) dx heeft wortels in diverse wetenschappelijke en technische domeinen. Van het analyseren van golfpatronen in de natuurkunde tot het modelleren van cyclische verschijnselen in de techniek, deze integraal duikt overal op waar trigonometrische functies een rol spelen.
Om de integraal van sin²(x) dx te ontcijferen, wenden we ons tot een essentiële trigonometrische identiteit: de dubbele-hoek formule. Deze formule stelt dat cos(2x) gelijk is aan 1 - 2sin²(x). Door deze formule te herschikken, kunnen we sin²(x) uitdrukken in termen van cos(2x), waardoor onze integraal transformeert in een meer handelbare vorm.
Met deze transformatie kunnen we de kracht van integratietechnieken aanwenden. Substitutie, een krachtig hulpmiddel in de calculus, stelt ons in staat om de integraal te vereenvoudigen en een elegante oplossing te vinden. Na integratie en substitutie komen we uit op de oplossing: (x/2) - (sin(2x)/4) + C.
De reis om de integraal van sin²(x) dx te begrijpen en op te lossen is een bewijs van de elegantie en kracht van calculus. Het is een concept dat ons uitdaagt om buiten de gebaande paden te denken, creativiteit te omarmen en de onderlinge verbondenheid van wiskundige ideeën te waarderen. Of je nu een student, een professional of gewoon een nieuwsgierige ziel bent, de wereld van de integratie heeft een schat aan kennis te bieden, wachtend om ontdekt te worden.
Voordelen van het begrijpen van de integraal van sin²(x) dx
Het begrijpen van de integraal van sin²(x) dx biedt verschillende voordelen:
- Verbeterd begrip van trigonometrie en calculus: Het beheersen van deze integraal verdiept je kennis van trigonometrische identiteiten en integratietechnieken.
- Toepassing in verschillende vakgebieden: De integraal van sin²(x) dx is essentieel in de natuurkunde, techniek en andere gebieden waar trigonometrische functies voorkomen.
- Verhoogd analytisch denkvermogen: Het oplossen van deze integraal vereist probleemoplossend vermogen en logisch redeneren, wat je analytische vaardigheden verbetert.
Veelgestelde vragen over de integraal van sin²(x) dx
Hier zijn enkele veelgestelde vragen over de integraal van sin²(x) dx:
- Wat is de integraal van sin²(x) dx?
De integraal van sin²(x) dx is (x/2) - (sin(2x)/4) + C, waarbij C een integratieconstante is.
- Welke trigonometrische identiteit wordt gebruikt bij het oplossen van deze integraal?
De dubbele-hoek formule voor cosinus, cos(2x) = 1 - 2sin²(x), wordt gebruikt om sin²(x) te herschrijven.
- Welke integratietechniek wordt meestal gebruikt om deze integraal op te lossen?
Substitutie is de meest gebruikte integratietechniek voor deze integraal.
- Waar wordt de integraal van sin²(x) dx in de praktijk toegepast?
Deze integraal wordt gebruikt bij het analyseren van golfpatronen, elektrische circuits, mechanische trillingen en andere fenomenen waarbij trigonometrische functies een rol spelen.
- Waarom is het belangrijk om de integratieconstante 'C' toe te voegen?
De integratieconstante 'C' vertegenwoordigt een willekeurige constante waarde die verloren gaat tijdens de differentiatie. Het toevoegen van 'C' zorgt voor een algemene oplossing voor de integraal.
- Zijn er andere manieren om de integraal van sin²(x) dx op te lossen?
Naast substitutie kan integratie door delen ook worden gebruikt, hoewel dit proces complexer kan zijn.
- Wat zijn enkele tips om integralen met trigonometrische functies op te lossen?
Enkele tips zijn: het beheersen van trigonometrische identiteiten, het herkennen van integratiepatronen en het oefenen met verschillende integratietechnieken.
- Waar kan ik meer informatie vinden over de integraal van sin²(x) dx en gerelateerde onderwerpen?
Online bronnen zoals Khan Academy, Wolfram Alpha en wiskundeboeken over calculus bieden uitgebreide informatie over dit onderwerp.
Conclusie
De integraal van sin²(x) dx is een prachtig voorbeeld van hoe calculus ons in staat stelt om complexe problemen op te lossen met behulp van elegante wiskundige hulpmiddelen. Door de kracht van trigonometrische identiteiten en integratietechnieken te benutten, kunnen we deze integraal oplossen en toepassen in diverse wetenschappelijke en technische disciplines. Het begrijpen van deze integraal en de toepassingen ervan opent de deur naar een dieper begrip van de wereld om ons heen, en benadrukt de schoonheid en relevantie van wiskunde in ons dagelijks leven. Of je nu een student, professional of gewoon een nieuwsgierige ziel bent, het verkennen van de wereld van calculus en trigonometrie biedt een lonende en boeiende intellectuele reis.
sin 2 x dx integration - Trees By Bike
sin 2 x dx integration - Trees By Bike
sin 2 x dx integration - Trees By Bike
Solved Find the indefinite integral. (Use C for the constant - Trees By Bike
sin 2 x dx integration - Trees By Bike
sin 2 x dx integration - Trees By Bike
sin 2 x dx integration - Trees By Bike
sin 2 x dx integration - Trees By Bike
sin 2 x dx integration - Trees By Bike
sin 2 x dx integration - Trees By Bike
sin 2 x dx integration - Trees By Bike
sin 2 x dx integration - Trees By Bike
sin 2 x dx integration - Trees By Bike
sin 2 x dx integration - Trees By Bike
sin 2 x dx integration - Trees By Bike