Ooit afgevraagd hoe die cijfertjes op je rekenmachine dansen als je deelt? Delen lijkt misschien een simpele rekensom, maar het is een fundamentele bouwsteen van de wiskunde. Van het eerlijk verdelen van snoepjes tot het berekenen van complexe formules, deling is overal aanwezig. Duik met ons in de fascinerende wereld van het delen van getallen en ontdek de geheimen achter deze essentiële rekenkundige operatie.
Getallen delen is meer dan alleen een sommetje op school. Het is een vaardigheid die je dagelijks gebruikt, vaak zonder erbij stil te staan. Denk aan het splitsen van de rekening in een restaurant, het berekenen van kortingen tijdens het shoppen of het verdelen van ingrediënten voor een recept. Begrijpen hoe deling werkt, geeft je meer controle over je financiën, helpt je bij het oplossen van dagelijkse problemen en vergroot je algemene rekenvaardigheid.
De geschiedenis van deling gaat ver terug. Al in de oudheid gebruikten beschavingen verschillende methoden om getallen te delen. Van Babylonische kleitabletten tot Egyptische hiërogliefen, de behoefte om te delen was altijd al aanwezig. Door de eeuwen heen zijn deze methoden verfijnd en gestandaardiseerd tot de technieken die we vandaag de dag gebruiken.
Het belang van deling kan niet worden overschat. Het vormt de basis voor vele andere wiskundige concepten, zoals breuken, percentages en verhoudingen. Zonder een goed begrip van deling is het moeilijk om verder te komen in de wiskunde en wetenschap. Het beheersen van deze vaardigheid opent deuren naar een wereld van kennis en mogelijkheden.
Een veelvoorkomend probleem bij het delen is het concept van restanten. Wat doe je met dat getal dat overblijft na de deling? Het begrijpen van restanten en hoe je ermee omgaat, is cruciaal voor het correct uitvoeren van delingen, vooral in praktische situaties. Denk bijvoorbeeld aan het verdelen van een aantal objecten over een groep mensen. De rest vertegenwoordigt het aantal objecten dat overblijft nadat iedereen een gelijk deel heeft ontvangen.
Delen is simpelweg het opsplitsen van een getal in gelijke delen. Het getal dat je deelt heet de deeltal, en het getal waardoor je deelt heet de deler. Het resultaat van de deling heet het quotiënt. Bijvoorbeeld, in de deling 12 : 3 = 4 is 12 de deeltal, 3 de deler en 4 het quotiënt.
Voorbeeld: Je hebt 15 koekjes en wilt ze gelijk verdelen over 5 vrienden. 15 : 5 = 3. Elke vriend krijgt 3 koekjes.
Voordelen van goed kunnen delen: 1. Beter begrip van wiskundige concepten. 2. Vermogen om dagelijkse problemen op te lossen. 3. Verhoogde zelfverzekerdheid in rekenvaardigheid.
Stap-voor-stap handleiding: 1. Schrijf de deeltal op. 2. Schrijf de deler op. 3. Voer de deling uit. 4. Schrijf het quotiënt op.
Voor- en Nadelen van Delen
Er zijn geen directe voor- of nadelen aan deling zelf, het is een neutrale wiskundige operatie. Echter, problemen kunnen ontstaan door verkeerd gebruik of misinterpretatie.
Vijf beste praktijken: 1. Oefen regelmatig. 2. Gebruik een rekenmachine voor complexe berekeningen. 3. Controleer je antwoord. 4. Leer de tafels van vermenigvuldiging. 5. Vraag om hulp als je het nodig hebt.
Vijf concrete voorbeelden: 1. 20 : 4 = 5. 2. 30 : 6 = 5. 3. 40 : 8 = 5. 4. 50 : 10 = 5. 5. 60 : 12 = 5.
FAQ: 1. Wat is deling? Antwoord: Het opsplitsen van een getal in gelijke delen. 2. Wat is een deler? Antwoord: Het getal waardoor je deelt. 3. Wat is een deeltal? Antwoord: Het getal dat je deelt. 4. Wat is een quotiënt? Antwoord: Het resultaat van de deling. 5. Wat is een rest? Antwoord: Het getal dat overblijft na de deling. 6. Hoe deel je met een rest? Antwoord: De rest wordt aangegeven naast het quotiënt. 7. Waar kan ik meer informatie vinden over deling? Antwoord: Online, in wiskundeboeken en op educatieve websites. 8. Hoe kan ik mijn delingsvaardigheden verbeteren? Antwoord: Door te oefenen en hulp te vragen wanneer nodig.
Tips en trucs: Leer de tafels van vermenigvuldiging. Gebruik een rekenmachine voor complexe berekeningen. Controleer altijd je antwoord.
Delen is een essentiële vaardigheid die ons helpt de wereld om ons heen te begrijpen. Van het splitsen van de rekening tot het uitvoeren van complexe wetenschappelijke berekeningen, deling speelt een cruciale rol in ons dagelijks leven. Door de basisprincipes te beheersen en te blijven oefenen, kunnen we onze rekenvaardigheden verbeteren en de magie van getallen ontsluiten. Dus, ga aan de slag, oefen met delingen en ontdek de eindeloze mogelijkheden die deze krachtige rekenkundige operatie te bieden heeft. Het beheersen van deling opent deuren naar een wereld van kennis en geeft je de tools om complexe problemen met vertrouwen aan te pakken. Blijf leren en ontdek de wonderen van de wiskunde!
Hoe Deel Je Een Breuk Tips En Tricks Voor Succes - Trees By Bike
Hoe Deel Je Een Breuk Tips En Tricks Voor Succes - Trees By Bike
Wat is het cijfer waard 2 - Trees By Bike
In deze video toont men je hoe je getallen leest en legt met losse - Trees By Bike
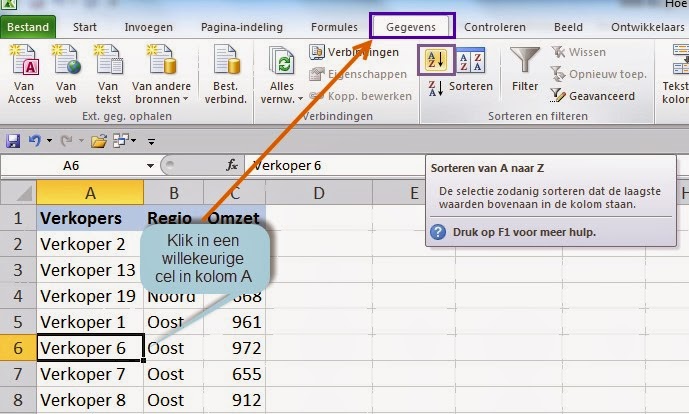
Sorteren van tekst met getallen - Trees By Bike
hoe deel je getallen - Trees By Bike
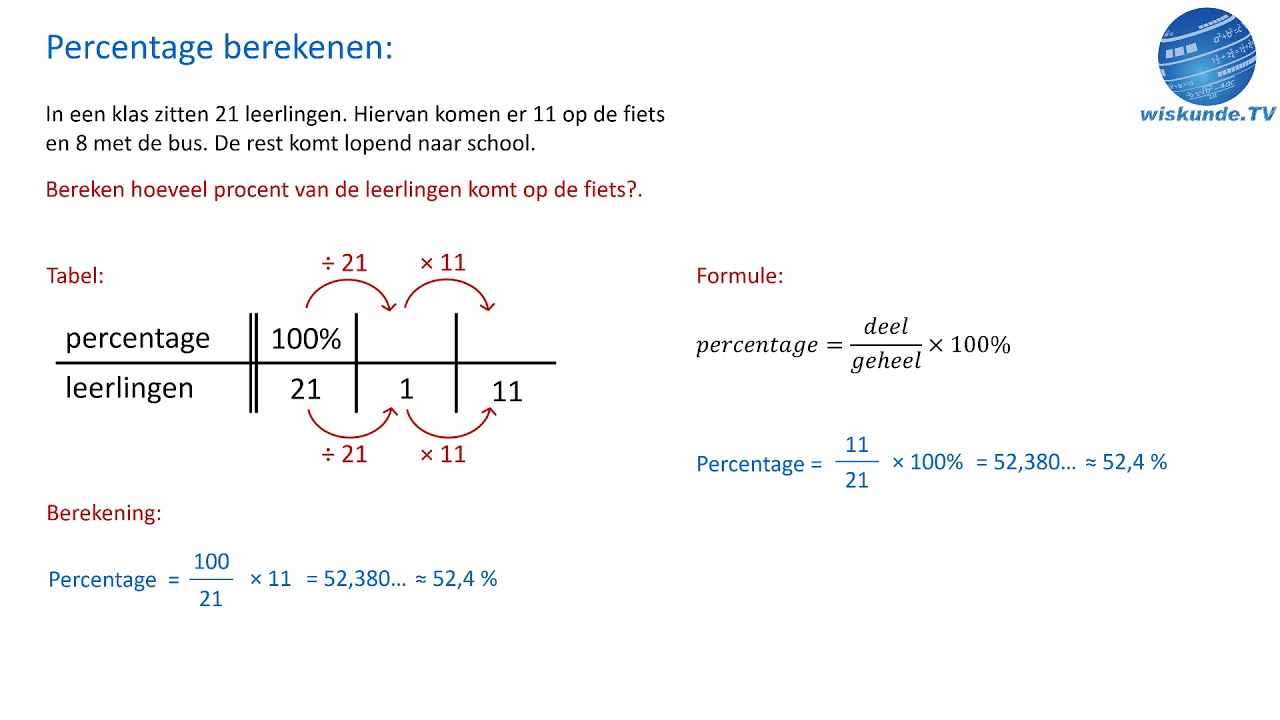
Hoe Bereken Je Een Percentage Van Een Geheel - Trees By Bike
Een breuk delen door een breuk middenbouw - Trees By Bike
hoe deel je getallen - Trees By Bike
Hoe Bereken Je Het Gemiddeld Eigen Vermogen - Trees By Bike
hoe deel je getallen - Trees By Bike
Een getal delen door een kommagetal groep7 - Trees By Bike
Rekenen grote deelsommen deel 1 - Trees By Bike
Schrijf het woord als getal - Trees By Bike
Samenvatting van Procenten uit Getal en Ruimte - Trees By Bike