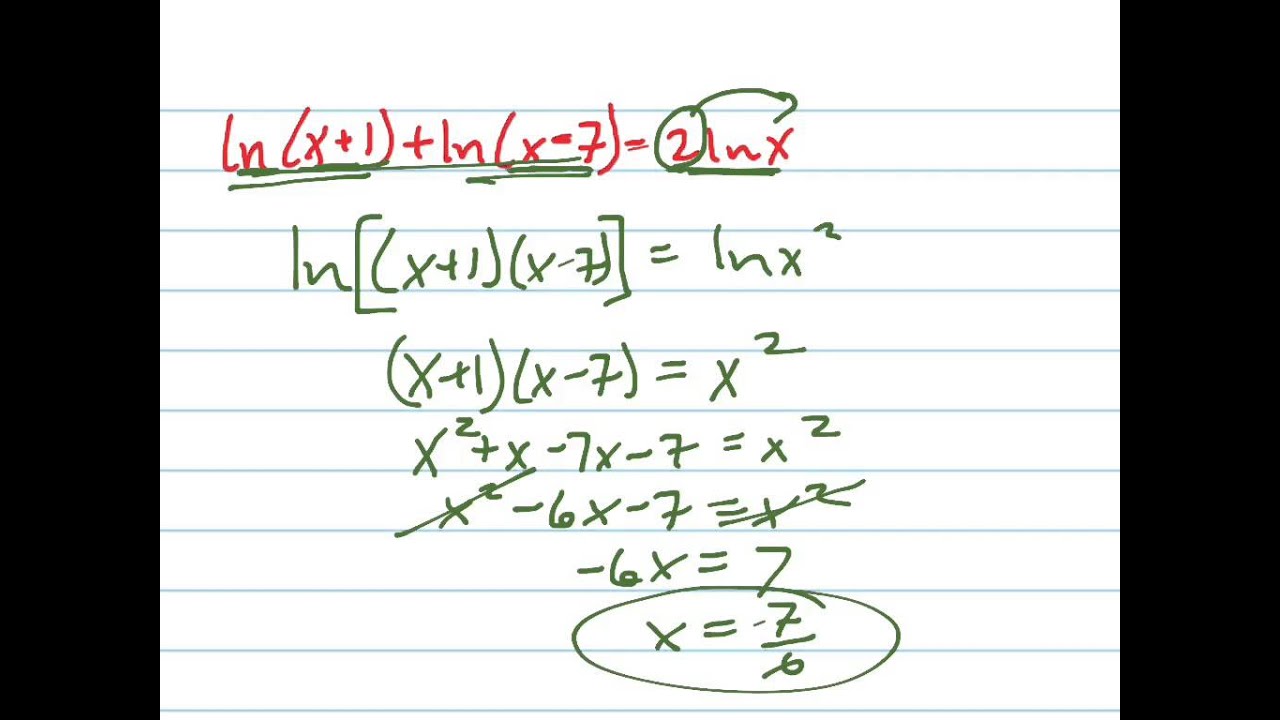De Magie van Logaritmen: Ontdek de Oplossing voor 2 ln x + 4 ln 2 = ln x

23 Aug 2024
nl
Emil

Wederom staren we naar een ogenschijnlijk complexe vergelijking, een wirwar van symbolen en getallen die ons uitdagen om de verborgen orde te ontrafelen. Vandaag wagen we ons in de fascinerende wereld van logaritmen, met als doel de oplossing te vinden voor de vergelijking 2 ln x + 4 ln 2 = ln x. Laat je niet afschrikken door de abstractie, want achter deze notatie schuilt een elegante logica die ons in staat stelt om complexe problemen op te lossen.

Logaritmen, vaak gezien als de tegenhanger van exponentiële functies, stellen ons in staat om te rekenen met machten en wortels op een geheel nieuwe manier. Ze bieden ons een krachtig hulpmiddel om te navigeren door de wereld van groei en verval, van de rente op een spaarrekening tot de halveringstijd van radioactief materiaal.

De geschiedenis van logaritmen gaat terug tot de 17e eeuw, met de Schot John Napier als pionier. Zijn doel was om complexe astronomische berekeningen te vereenvoudigen, en zijn uitvinding had een enorme impact op de ontwikkeling van de wiskunde, natuurkunde en astronomie. Vandaag de dag, in ons digitale tijdperk, zijn logaritmen alomtegenwoordig, van algoritmen voor zoekmachines tot datacompressie en signaalverwerking.

Maar laten we terugkeren naar onze uitdaging: het oplossen van de vergelijking 2 ln x + 4 ln 2 = ln x. Om dit te doen, moeten we ons vertrouwd maken met enkele basisregels van logaritmen. Eerst en vooral, de logaritme van een product is gelijk aan de som van de logaritmen van de factoren. Dit betekent dat ln(a*b) = ln a + ln b. Daarnaast geldt dat de logaritme van een macht gelijk is aan de exponent vermenigvuldigd met de logaritme van het grondtal. Dus ln(a^b) = b * ln a.

Gewapend met deze kennis kunnen we onze vergelijking vereenvoudigen. We beginnen met het herschrijven van 4 ln 2 als ln(2^4), wat gelijk is aan ln 16. Onze vergelijking wordt dan 2 ln x + ln 16 = ln x. Vervolgens brengen we alle termen met ln x naar de linkerkant van de vergelijking: 2 ln x - ln x + ln 16 = 0. Dit vereenvoudigen we tot ln x + ln 16 = 0. Nu kunnen we de regel ln(a*b) = ln a + ln b toepassen om ln(16x) = 0 te krijgen. Om de logaritme te verwijderen, gebruiken we de inverse functie, de exponentiële functie: e^(ln(16x)) = e^0. Dit geeft ons 16x = 1. Tenslotte delen we beide kanten door 16 om de oplossing te vinden: x = 1/16.

Het oplossen van deze vergelijking is niet alleen een kwestie van het toepassen van regels, maar ook van het begrijpen van de onderliggende principes. Door de eigenschappen van logaritmen te beheersen, kunnen we complexe vergelijkingen ontleden en vereenvoudigen, waardoor we elegante oplossingen vinden voor ogenschijnlijk onoverkomelijke problemen.

De reis door de wereld van logaritmen is een fascinerende. Het is een wereld waar abstracte concepten tot leven komen en waar wiskundige elegantie hand in hand gaat met praktische toepassingen. Dus, de volgende keer dat je een logaritme tegenkomt, wees dan niet bang. Zie het als een uitdaging, een kans om je analytische vaardigheden aan te scherpen en de verborgen schoonheid van wiskunde te ontdekken.