Stel je voor: een vorm, symmetrisch en toch dynamisch, met vijf gelijke zijden en vijf gelijke hoeken. Dat is de vijfhoek, een geometrische figuur die al eeuwenlang de mens fascineert. Van de stervormige varianten tot de regelmatige vijfhoeken die we terugvinden in architectuur en design, de vijfhoek is een vorm met een rijke geschiedenis en een verrassende veelzijdigheid.
Maar hoe teken je nu precies een vijfhoek? Welke methoden zijn er en welke gereedschappen heb je nodig? En wat maakt de vijfhoek zo bijzonder in de wiskunde en in onze belevingswereld?
In dit artikel nemen we je mee op ontdekkingsreis door de wereld van de vijfhoek. We duiken in de geschiedenis van deze vorm, ontrafelen de wiskundige eigenschappen en laten zien hoe je zelf, stap voor stap, een perfecte vijfhoek kunt tekenen.
Bereid je voor om verrast te worden door de schoonheid en de veelzijdigheid van de vijfhoek. We zullen zien dat deze ogenschijnlijk eenvoudige vorm een schat aan interessante eigenschappen en toepassingen herbergt. Van de Pentagon in Washington D.C. tot de vijfhoekige patronen in de natuur, de vijfhoek is overal om ons heen.
Dus, pak je kompas en liniaal erbij en laat je meenemen op deze fascinerende reis door de wereld van de geometrie!
Voor- en nadelen van het begrijpen van de vijfhoek
Hoewel de vijfhoek een abstracte geometrische vorm is, heeft het begrijpen ervan wel degelijk voordelen:
| Voordelen | Nadelen |
|---|---|
| Vergroot je ruimtelijk inzicht | Vereist enige wiskundige kennis |
| Opent de deur naar de wereld van geometrie | - |
| Kan nuttig zijn bij praktische toepassingen, zoals tekenen en ontwerpen | - |
Vijf beste praktijken voor het tekenen van een vijfhoek
Hier zijn vijf beproefde methoden om een perfecte vijfhoek te creëren:
- Met passer en liniaal: Deze klassieke methode is zeer nauwkeurig en relatief eenvoudig te leren.
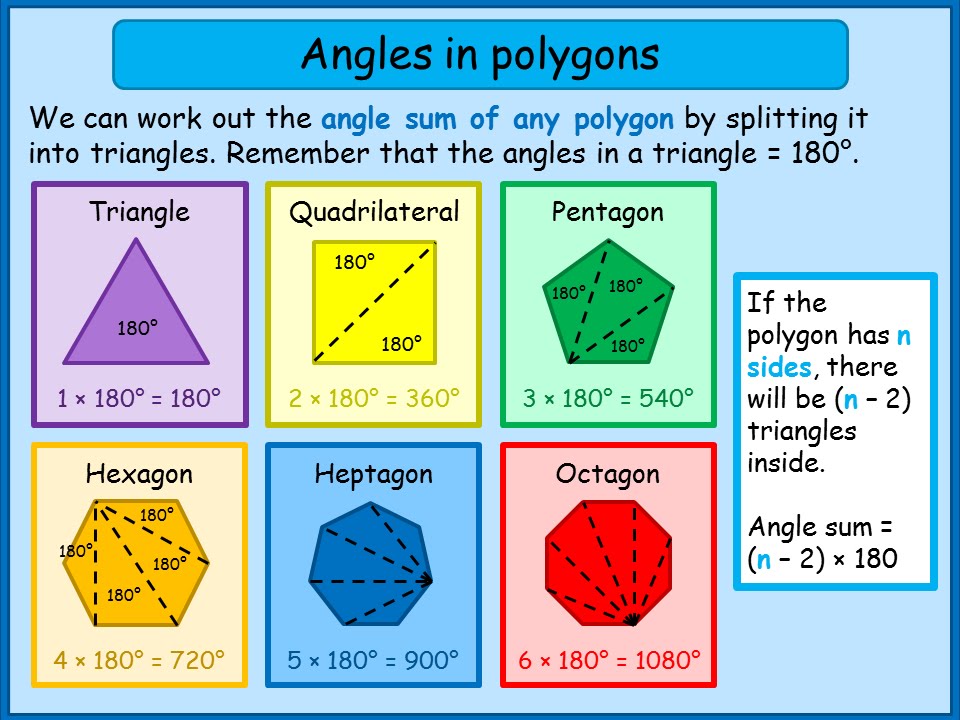
- Met een gradenboog en liniaal: Meet de hoeken van de vijfhoek (elk 108 graden) en teken de zijden met behulp van een liniaal.
- Door vouwen van papier: Een leuke en praktische manier om een regelmatige vijfhoek te maken zonder gereedschap.
- Met behulp van digitale tools: Ontwerpsoftware zoals Adobe Illustrator biedt precieze tools voor het tekenen van vijfhoeken.
- Met behulp van sjablonen: Handig voor snel en eenvoudig tekenen van identieke vijfhoeken.
Vijf concrete voorbeelden van vijfhoeken in de wereld om ons heen
- Het Pentagon: Het beroemde gebouw van het Amerikaanse ministerie van Defensie dankt zijn naam aan zijn vijfhoekige vorm.
- Stervrucht: Deze exotische vrucht heeft een opvallende stervormige doorsnede, die eigenlijk een vijfhoek is.
- Verkeersborden: Sommige verkeersborden, zoals het stopbord, hebben een vijfhoekige vorm om de zichtbaarheid te vergroten.
- Voetballen: De traditionele voetbal is opgebouwd uit vijfhoeken en zeshoeken.
- Kristallen: Sommige mineralen vormen kristallen met een vijfhoekige structuur, zoals pyriet.
Vijf veelgestelde vragen over de vijfhoek
Hier zijn enkele veelgestelde vragen en antwoorden over de vijfhoek:
- Vraag: Hoeveel graden heeft een hoek van een regelmatige vijfhoek?
Antwoord: Elke hoek van een regelmatige vijfhoek heeft een hoek van 108 graden. - Vraag: Wat is de formule voor de oppervlakte van een regelmatige vijfhoek?
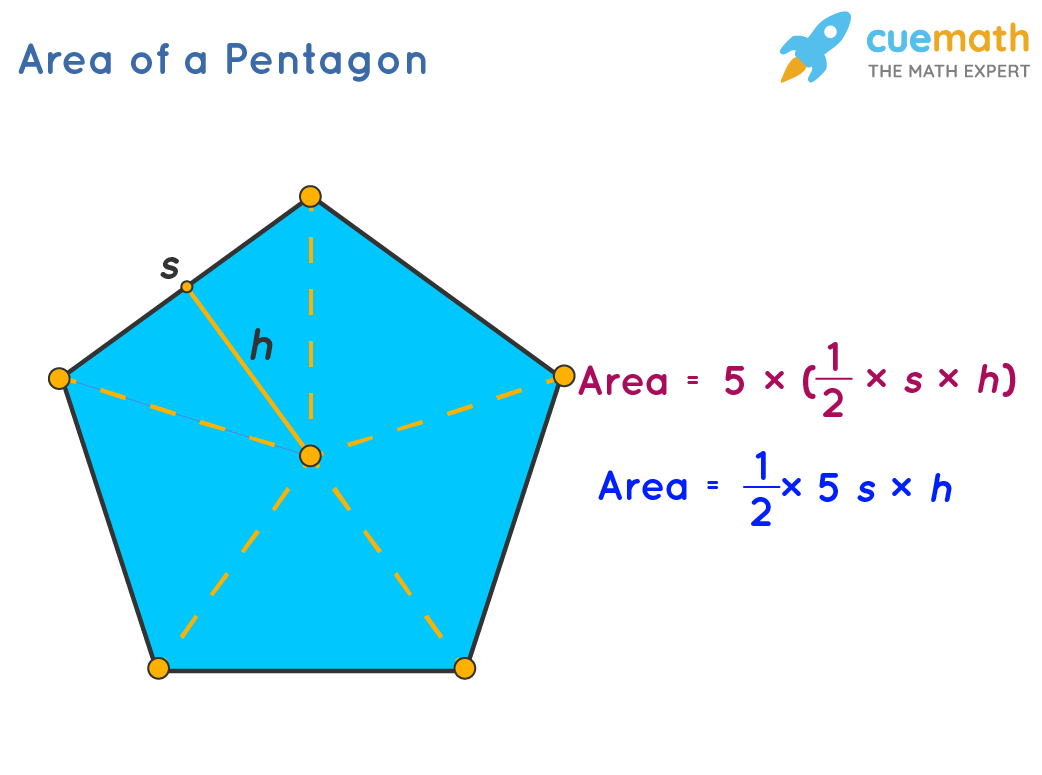
Antwoord: De oppervlakte (A) van een regelmatige vijfhoek wordt berekend met de formule A = (1/4)√(5(5+2√5)) * s², waarbij s de lengte van een zijde is. - Vraag: Wat is de Gulden Snede en heeft het iets te maken met de vijfhoek?
Antwoord: Ja, de Gulden Snede (ongeveer 1,618) is een wiskundige verhouding die terug te vinden is in de verhoudingen van een regelmatige vijfhoek. - Vraag: Waar kan ik meer informatie vinden over de vijfhoek?
Antwoord: Online bronnen zoals Wikipedia, wiskundewebsites en educatieve YouTube-kanalen bieden een schat aan informatie over de vijfhoek. - Vraag: Wat zijn enkele leuke activiteiten om meer te leren over de vijfhoek?
Antwoord: Probeer zelf een vijfhoek te tekenen met verschillende methoden, zoek naar voorbeelden van vijfhoeken in je omgeving of maak een kunstwerk geïnspireerd op deze fascinerende vorm.
Conclusie
De vijfhoek, een vorm die eenvoud en complexiteit combineert, heeft ons meegenomen op een boeiende reis door de wereld van de geometrie. We hebben de geschiedenis verkend, de wiskundige eigenschappen ontrafeld en praktische toepassingen ontdekt. Van het tekenen van een perfecte vijfhoek met passer en liniaal tot het herkennen van de vorm in architectuur en natuur, we hebben gezien dat de vijfhoek overal om ons heen aanwezig is. Of je nu een student bent die zich verdiept in de wiskunde, een kunstenaar die op zoek is naar inspiratie of gewoon nieuwsgierig bent naar de wereld om je heen, de vijfhoek heeft voor ieder wat wils. Dus, de volgende keer dat je een vijfhoek tegenkomt, neem dan even de tijd om de schoonheid en de complexiteit van deze fascinerende vorm te waarderen.
show me a shape of a pentagon - Trees By Bike
show me a shape of a pentagon - Trees By Bike
Maths Shapes For Kids - Trees By Bike
Measure Of Angles In Polygons - Trees By Bike
Vecteur Stock Types of regular polygons. Triangle, Quadrilateral - Trees By Bike
show me a shape of a pentagon - Trees By Bike
show me a shape of a pentagon - Trees By Bike
show me a shape of a pentagon - Trees By Bike
Complex 2D Geometric Shapes - Trees By Bike
show me a shape of a pentagon - Trees By Bike
show me a shape of a pentagon - Trees By Bike
New Material Stronger Than Diamond at Shawn Bryant blog - Trees By Bike
Creating And Subdividing Polygons - Trees By Bike
Road Signs Jeopardy Template - Trees By Bike
show me a shape of a pentagon - Trees By Bike