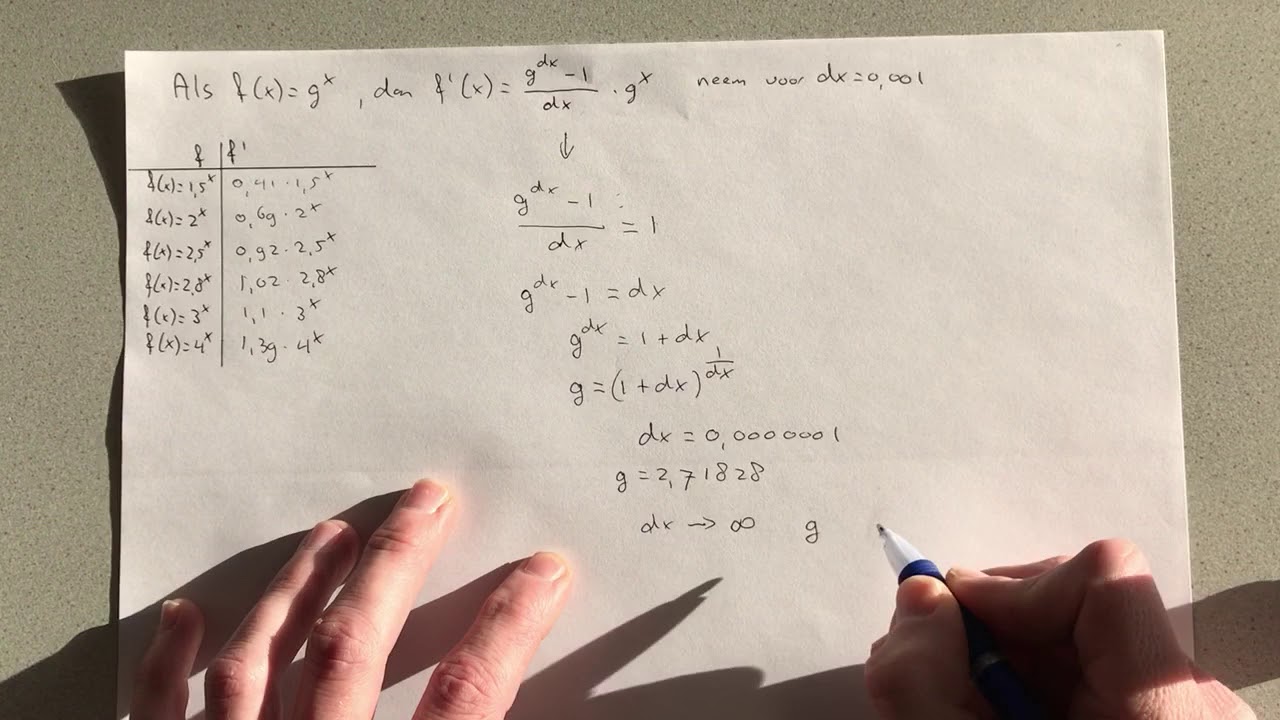De wiskundige constante 'e', ook wel het getal van Euler genoemd, is al eeuwenlang een bron van fascinatie voor wiskundigen. Met een waarde van ongeveer 2.71828, speelt 'e' een essentiële rol in diverse wetenschappelijke disciplines, waaronder natuurkunde, biologie en economie. Een van de meest voorkomende toepassingen van 'e' is in de functie 'e tot de macht x', die vaak wordt gebruikt om exponentiële groei en verval te modelleren.
Het begrijpen van 'e tot de macht x' gaat verder dan alleen het kunnen berekenen. Het gaat om het doorgronden van de inherente schoonheid en elegantie van deze functie, en de impact ervan op ons begrip van de wereld om ons heen.
In deze uitgebreide gids duiken we in de wereld van 'e tot de macht x'. We verkennen de geschiedenis van deze fascinerende functie, de oorsprong van de constante 'e', en de redenen waarom deze functie zo belangrijk is in verschillende toepassingen. Bereid je voor om ondergedompeld te worden in de wonderlijke wereld van exponentiële groei en verval, en ontdek de kracht van 'e tot de macht x'.
Van het modelleren van bacteriële groei tot het voorspellen van radioactief verval, 'e tot de macht x' speelt een cruciale rol in ons begrip van dynamische processen. Door de principes van deze functie te begrijpen, kunnen we de complexiteit van de wereld om ons heen beter interpreteren en analyseren.
Of je nu een student bent die worstelt met wiskunde, een professional die de kracht van exponentiële functies wil benutten, of gewoon nieuwsgierig bent naar de elegantie van wiskunde, deze gids biedt een toegankelijke en boeiende verkenning van 'e tot de macht x'.
Voordelen van het begrijpen van 'e tot de macht x'
Het beheersen van 'e tot de macht x' biedt tal van voordelen, waaronder:
| Voordeel | Uitleg |
|---|---|
| Modelleren van natuurlijke fenomenen | Van bevolkingsgroei tot radioactief verval, 'e tot de macht x' is essentieel voor het beschrijven van talloze natuurlijke processen. |
| Financiële berekeningen | Bij het berekenen van samengestelde rente en andere financiële modellen speelt 'e tot de macht x' een cruciale rol. |
| Problemen oplossen in diverse wetenschappelijke disciplines | Van natuurkunde tot biologie, 'e tot de macht x' is een onmisbaar instrument in de wetenschap. |
Veelgestelde vragen over 'e tot de macht x'
Wat is de afgeleide van e^x?
De afgeleide van e^x is, elegant genoeg, e^x zelf.
Wat is de integraal van e^x?
De integraal van e^x is, eveneens, e^x + C, waarbij C een integratieconstante is.
Wat is de waarde van e^0?
Elke getal tot de macht 0 is gelijk aan 1, dus e^0 = 1.
Hoe los ik vergelijkingen op met e^x?
Het oplossen van vergelijkingen met e^x kan complex zijn, maar vaak wordt de natuurlijke logaritme (ln) gebruikt om x te isoleren.
Wat zijn enkele toepassingen van e^x in het dagelijks leven?
Naast de eerder genoemde voorbeelden, wordt e^x gebruikt in gebieden als muziek, computergraphics en signaalverwerking.
'E tot de macht x' is meer dan alleen een wiskundige functie - het is een venster naar een wereld van exponentiële groei en verval, een sleutel tot het begrijpen van de dynamiek van onze natuurlijke wereld en een essentieel instrument in talloze wetenschappelijke disciplines. Door de principes van deze fascinerende functie te doorgronden, openen we de deur naar een dieper begrip van de wereld om ons heen.
e tot de macht x oplossen - Trees By Bike
e tot de macht x oplossen - Trees By Bike
Videoplatform :: Afgeleide: Differentiëren - Trees By Bike
e tot de macht x oplossen - Trees By Bike
Machten met negatief grondtal. Inzicht - Trees By Bike
e tot de macht x oplossen - Trees By Bike
e tot de macht x oplossen - Trees By Bike
e tot de macht x oplossen - Trees By Bike
e tot de macht x oplossen - Trees By Bike
Het Kwadraat Van 7 Plus 11: Rekenkundig Vraagstuk Opgelost - Trees By Bike
Klinge Bereit Notizbuch rekenen met machten regels Analytisch Die ganze - Trees By Bike
e tot de macht x oplossen - Trees By Bike
2020 bmw x1 catalog.pdf (5.89 MB) - Trees By Bike
e tot de macht x oplossen - Trees By Bike
e tot de macht x oplossen - Trees By Bike