Hoe bereken je graden? Een vraag die velen bezighoudt, van scholieren die worstelen met meetkunde tot professionals die complexe berekeningen uitvoeren. Deze gids biedt een diepgaande blik op de verschillende manieren om graden te berekenen, ongeacht de context.
Het bepalen van graden is essentieel in diverse vakgebieden, zoals wiskunde, natuurkunde, engineering en architectuur. Of het nu gaat om het berekenen van hoeken in een driehoek, de helling van een dak, of de baan van een satelliet, de juiste kennis van gradenberekening is cruciaal.
Van gradenbogen tot geavanceerde trigonometrische functies, er zijn diverse methoden om graden te berekenen. Deze gids behandelt zowel eenvoudige als complexe berekeningen, met heldere voorbeelden en praktische tips.
Deze gids biedt niet alleen een overzicht van de verschillende methoden, maar duikt ook dieper in de geschiedenis en het belang van gradenberekening. We verkennen de oorsprong van het graden-systeem en de impact ervan op wetenschap en technologie.
Of je nu een student bent die extra hulp nodig heeft bij huiswerk, een professional die zijn kennis wil opfrissen, of gewoon nieuwsgierig bent naar het concept van gradenberekening, deze gids biedt waardevolle inzichten en praktische tools.
Het concept van graden is ontstaan in de oude beschavingen van Mesopotamië en Egypte, waar men de noodzaak zag om hoeken en richtingen te meten. Het 360-gradensysteem, zoals we dat vandaag kennen, wordt vaak toegeschreven aan de Babyloniërs, vanwege hun gebruik van een zestigtallig (base-60) telsysteem.
Graden spelen een cruciale rol in de trigonometrie, de tak van wiskunde die zich bezighoudt met de relaties tussen hoeken en zijden van driehoeken. Met behulp van trigonometrische functies zoals sinus, cosinus en tangens kunnen we graden berekenen in verschillende geometrische figuren.
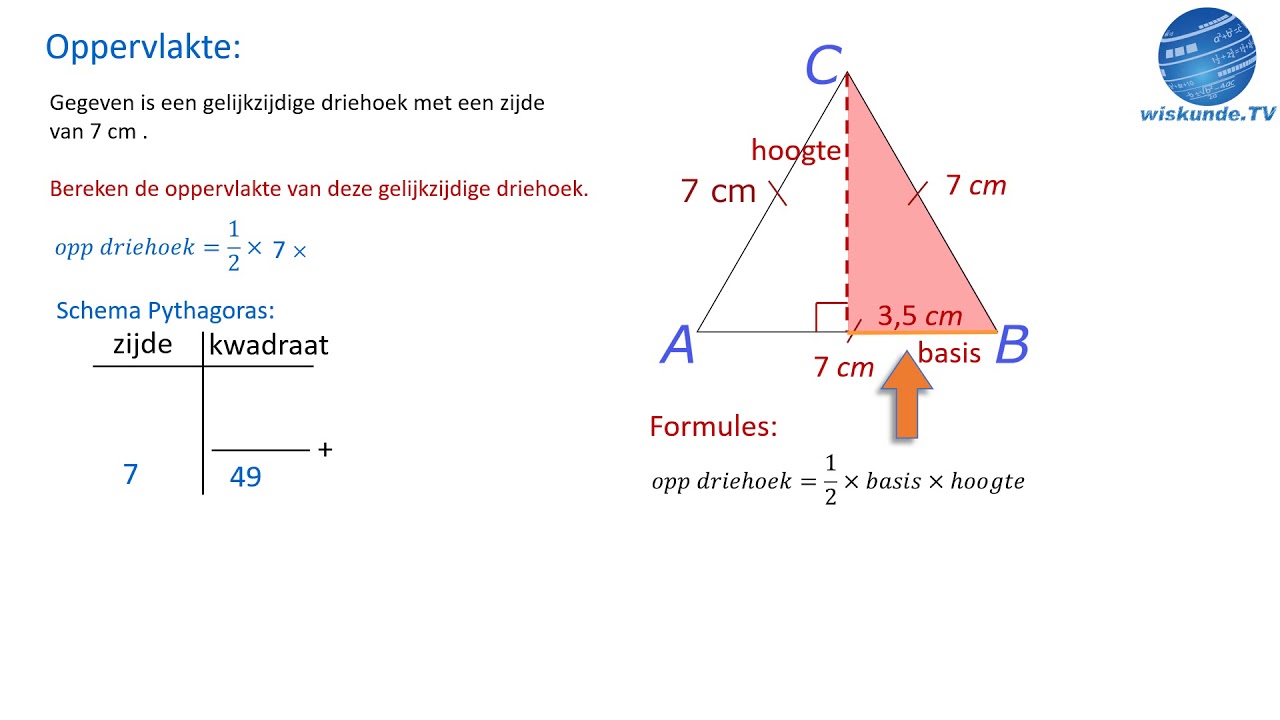
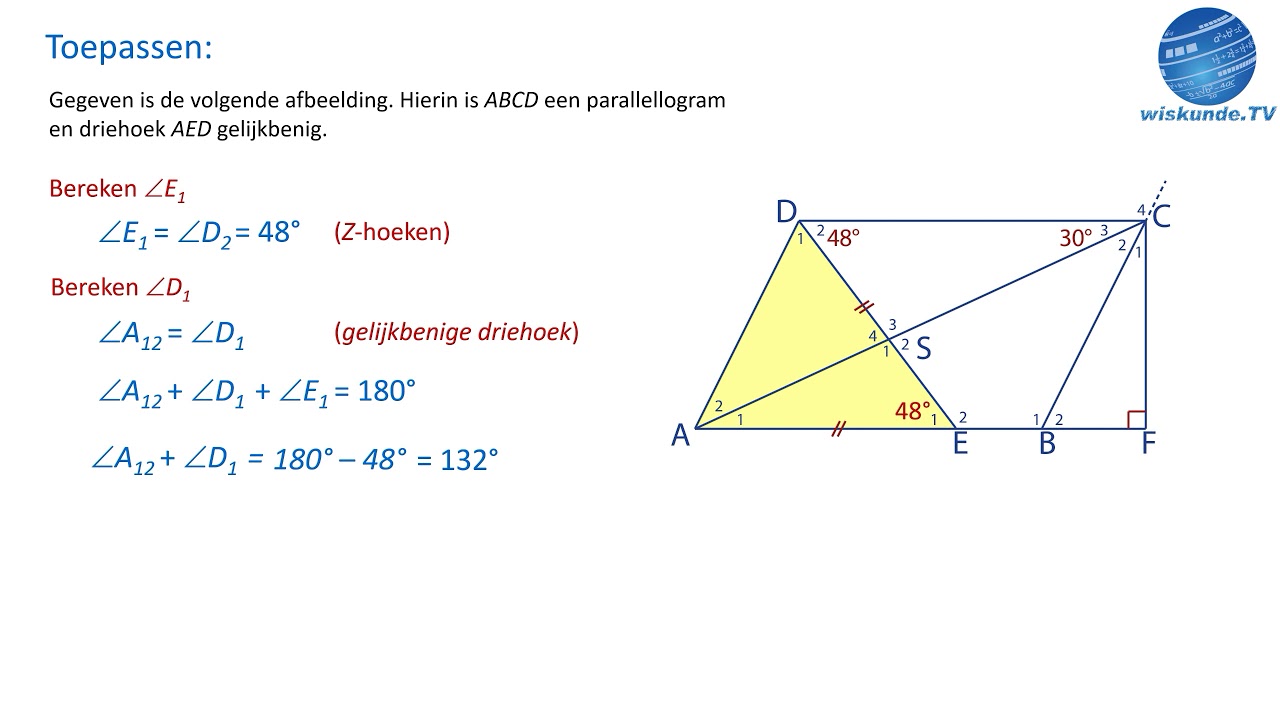
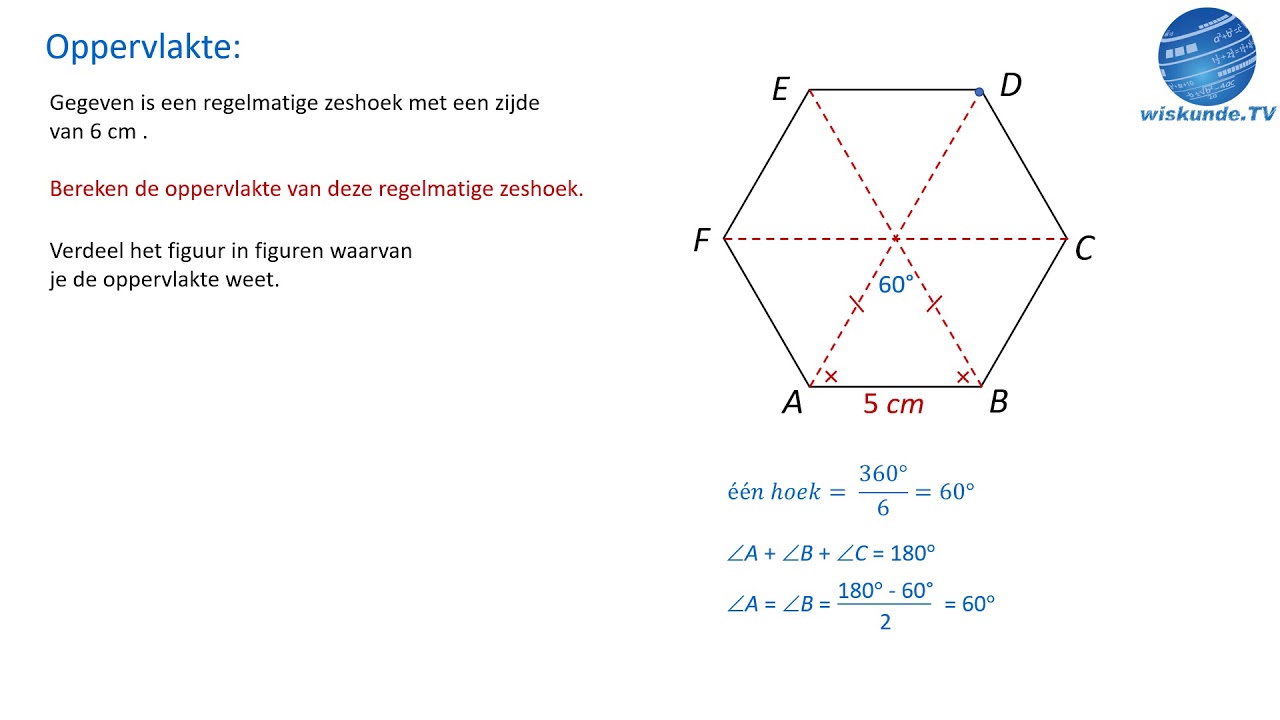
Een eenvoudig voorbeeld van gradenberekening is het bepalen van de hoeken in een driehoek. De som van de binnenhoeken van een driehoek is altijd 180 graden. Als we twee hoeken kennen, kunnen we de derde hoek berekenen door 180 graden te verminderen met de som van de twee bekende hoeken.
Voordelen van het begrijpen van gradenberekening zijn:
1. Nauwkeurige metingen in constructie en engineering.
2. Het oplossen van complexe geometrische problemen.
3. Beter begrip van navigatie en cartografie.
Een stap-voor-stap handleiding voor het berekenen van een onbekende hoek in een driehoek: 1. Tel de twee bekende hoeken bij elkaar op. 2. Trek de som van de bekende hoeken af van 180 graden. Het resultaat is de onbekende hoek.
Voor- en Nadelen van het Gradensysteem
Er zijn geen directe voor- en nadelen aan het gradensysteem zelf, maar eerder aan de context van het gebruik. De keuze voor graden of radialen (een alternatieve eenheid voor hoeken) hangt af van de specifieke toepassing.
Veelgestelde vragen:
1. Wat is een graad? Een graad is een eenheid voor het meten van hoeken.
2. Hoeveel graden zijn er in een cirkel? 360 graden.
3. Wat is de relatie tussen graden en radialen? 360 graden is gelijk aan 2π radialen.
4. Hoe bereken je de hoek van een rechthoekige driehoek? Gebruik de stelling van Pythagoras.
5. Wat is de som van de hoeken in een vierhoek? 360 graden.
6. Hoe bereken ik de hoek van een helling? Gebruik trigonometrie (tangens).
7. Wat zijn complementaire hoeken? Twee hoeken die samen 90 graden vormen.
8. Wat zijn supplementaire hoeken? Twee hoeken die samen 180 graden vormen.
Tip: Oefen met verschillende voorbeelden om je vaardigheden in gradenberekening te verbeteren.
Conclusie: Het berekenen van graden is een fundamentele vaardigheid met brede toepassingen in diverse disciplines. Van eenvoudige meetkundige berekeningen tot complexe engineering projecten, een goed begrip van graden is essentieel. Door de verschillende methoden en technieken te beheersen die in deze gids worden beschreven, kunnen zowel studenten als professionals hun vaardigheden verbeteren en succes behalen in hun respectievelijke vakgebieden. Het is belangrijk om te blijven oefenen met verschillende voorbeelden en de concepten toe te passen in real-world situaties om een diepgaand begrip te ontwikkelen en de volledige potentie van gradenberekening te benutten. Blijf leren en ontdek de fascinerende wereld van hoeken en graden!
hoe bereken je graden - Trees By Bike
hoe bereken je graden - Trees By Bike
Hoe Bereken Je Vierkante Meter - Trees By Bike
Hoe Bereken Je Gemiddeld Uit - Trees By Bike
Van Graden naar Radialen - Trees By Bike
What Is Cosinus And Sinus - Trees By Bike
Hoe Bereken Je Km Per Uur Een Eenvoudige Handleiding - Trees By Bike
Hoe Bereken Je De Graden Van Een Hoek Eenvoudige Uitleg - Trees By Bike
Hoe typ je graden celcius C - Trees By Bike
Hoe Bereken Je De Oppervlakte Van Een Rechthoek Een Simpele Gids - Trees By Bike
Hoe typ je het graden teken op je laptop - Trees By Bike
Hoe Bereken Ik Een Vierkante Meter - Trees By Bike
hoe bereken je graden - Trees By Bike
Inhoud van cilinder berekenen - Trees By Bike
hoe bereken je een hoek Berekenen hoek sinus met - Trees By Bike