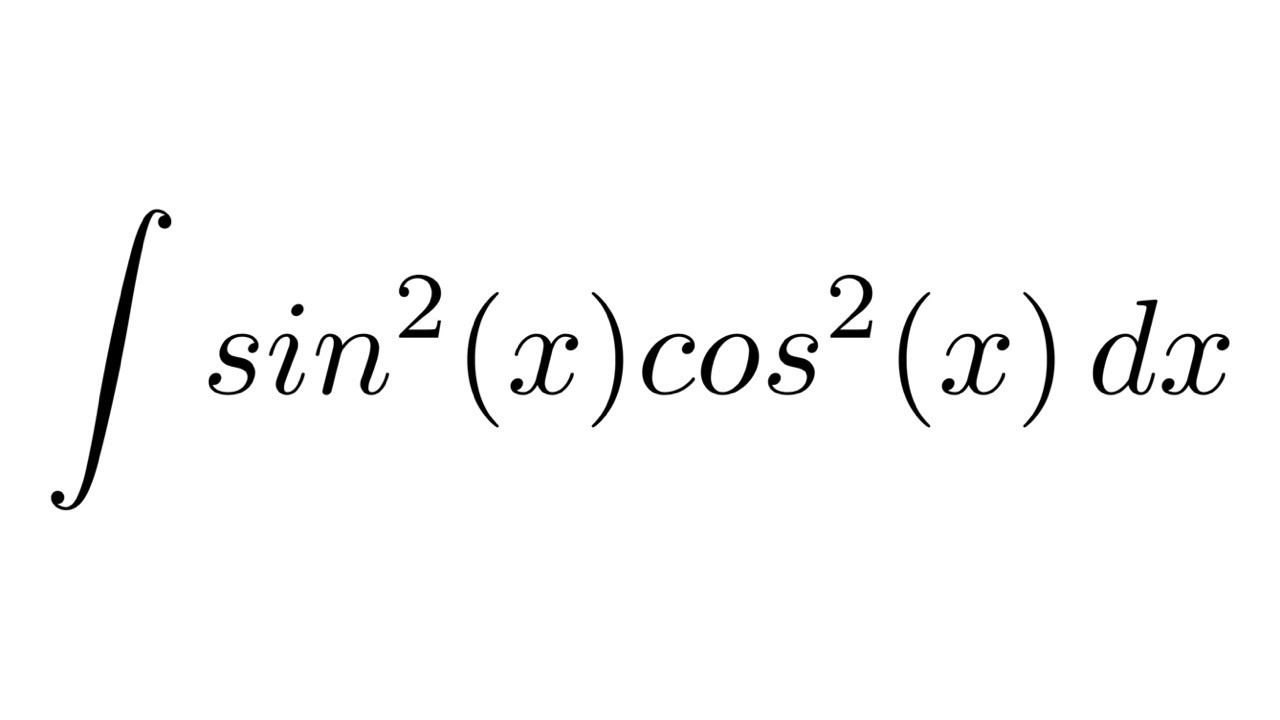De wereld van de wiskunde zit vol elegante vergelijkingen en expressies die, op het eerste gezicht, misschien complex lijken, maar bij nadere beschouwing een wereld van kennis en toepassingen ontsluiten. Eén zo'n expressie is de integraal van sin x cos x dx. Hoewel het er voor sommigen misschien uitziet als een wirwar van symbolen, heeft deze integraal een lange geschiedenis en een breed scala aan toepassingen in verschillende wetenschappelijke disciplines.
De integraal van sin x cos x dx vindt zijn oorsprong in de calculus, een belangrijk onderdeel van de wiskunde dat zich bezighoudt met verandering. Het concept van integratie, weergegeven door het ∫-symbool, is nauw verbonden met het vinden van oppervlakten, volumes en andere belangrijke grootheden. In het geval van sin x cos x dx, zoeken we naar de functie waarvan de afgeleide sin x cos x is.
Om de integraal van sin x cos x dx te berekenen, kunnen we gebruik maken van de substitutiemethode. Door u = sin x te stellen, wordt du = cos x dx. De integraal wordt dan ∫ u du, wat een eenvoudige integraal is die resulteert in u²/2 + C. Door u terug te substitueren, krijgen we de uiteindelijke oplossing: (sin²x)/2 + C, waarbij C de integratieconstante is.
De schoonheid van de integraal van sin x cos x dx ligt niet alleen in de elegante oplossing, maar ook in de talloze toepassingen. In de natuurkunde wordt deze integraal gebruikt om bijvoorbeeld de arbeid te berekenen die wordt verricht door een variabele kracht, of om de energie van een oscillerende veer te bepalen. In de elektrotechniek is de integraal van sin x cos x dx essentieel voor het analyseren van wisselstroomcircuits.
Hoewel de berekening van integralen soms complex kan lijken, zijn er hulpmiddelen beschikbaar die het proces kunnen vereenvoudigen. Tabellen met integralen, software zoals Wolfram Alpha en online calculators kunnen van onschatbare waarde zijn voor studenten en professionals.
Het begrijpen van integralen, zoals de integraal van sin x cos x dx, is essentieel voor iedereen die zich bezighoudt met wiskunde, natuurkunde, engineering of andere wetenschappelijke disciplines. Door de principes van integratie onder de knie te krijgen, openen zich deuren naar een dieper begrip van de wereld om ons heen.
Voor- en Nadelen van Integral Sin x Cos x dx
Hoewel er geen directe voor- of nadelen zijn aan een wiskundige expressie zoals de integraal van sin x cos x dx, kunnen we de voor- en nadelen bespreken van het begrijpen en kunnen toepassen van integralen in het algemeen:
| Voordelen | Nadelen |
|---|---|
| Krachtig hulpmiddel voor het oplossen van complexe problemen in verschillende wetenschappelijke disciplines. | Vereist een gedegen kennis van calculus en kan voor beginners uitdagend zijn. |
| Opent deuren naar een dieper begrip van de wereld om ons heen. | Kan tijdrovend zijn om te leren en te beheersen. |
| Essentieel voor carrières in STEM-gebieden (Science, Technology, Engineering, and Mathematics). | Niet altijd direct toepasbaar in alledaagse situaties. |
De integraal van sin x cos x dx, hoewel een specifiek voorbeeld, dient als een toegangspoort tot de bredere wereld van calculus en de kracht van wiskundige modellering. Het beheersen van dit concept, samen met andere fundamentele principes van calculus, opent deuren naar een dieper begrip van de wereld om ons heen en biedt een solide basis voor verdere verkenning in de wiskunde en wetenschap.
integral sin x cos x dx - Trees By Bike
integral sin x cos x dx - Trees By Bike
integral sin x cos x dx - Trees By Bike
integral sin x cos x dx - Trees By Bike
integral sin x cos x dx - Trees By Bike
integral sin x cos x dx - Trees By Bike
integral sin x cos x dx - Trees By Bike
integral sin x cos x dx - Trees By Bike
integral sin x cos x dx - Trees By Bike
integral sin x cos x dx - Trees By Bike
integral sin x cos x dx - Trees By Bike
integral sin x cos x dx - Trees By Bike
integral sin x cos x dx - Trees By Bike
integral sin x cos x dx - Trees By Bike
integral sin x cos x dx - Trees By Bike