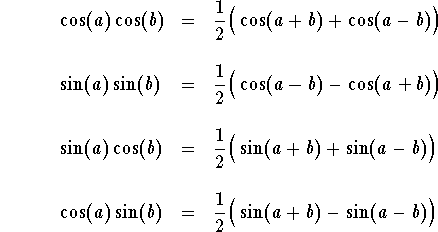Ontdek de kracht van de 2 sin a cos b formule in de trigonometrie

11 Oct 2024
nl
Emil

Stel je voor: je bent een ontdekkingsreiziger die navigeert door de oceaan, een ingenieur die de akoestiek van een concertzaal optimaliseert of een programmeur die realistische graphics creëert. Wat hebben deze scenario's met elkaar gemeen? Ze vertrouwen allemaal op de elegante kracht van trigonometrie, en in het bijzonder, de formule 2 sin a cos b.

De formule 2 sin a cos b, ook wel bekend als de dubbele-hoek formule voor sinus, is een essentieel hulpmiddel in de wiskunde en haar toepassingen. Het verbindt de sinus en cosinus van twee hoeken, a en b, met de sinus van hun som. Hoewel het op het eerste gezicht misschien abstract lijkt, heeft deze formule een breed scala aan toepassingen in de echte wereld.

De geschiedenis van de formule gaat terug tot de oude Grieken, die de basis legden voor de trigonometrie. Ze gebruikten deze principes voor navigatie, astronomie en architectuur. De formule 2 sin a cos b is een bewijs van hun genialiteit en de blijvende impact van hun ontdekkingen.

Een van de belangrijkste problemen die deze formule aanpakt, is de noodzaak om trigonometrische functies te vereenvoudigen en te manipuleren. Door de sinus van een som van hoeken uit te drukken in termen van sinus en cosinus van de individuele hoeken, opent de formule deuren naar het oplossen van complexe vergelijkingen en het bewijzen van trigonometrische identiteiten.

De formule 2 sin a cos b is veel meer dan een wiskundige curiositeit. Het is een onmisbaar instrument in verschillende disciplines, waaronder:

Natuurkunde: van het beschrijven van de beweging van golven tot het analyseren van elektrische circuits, de formule speelt een cruciale rol in het modelleren en begrijpen van fysische verschijnselen.
Engineering: het ontwerp van bruggen, gebouwen en andere structuren vereist een grondige kennis van krachten en belastingen, die vaak worden berekend met behulp van trigonometrische formules zoals 2 sin a cos b.
Computerwetenschappen: van het creëren van realistische graphics tot het ontwikkelen van algoritmen voor kunstmatige intelligentie, de formule vindt toepassingen in verschillende gebieden van de informatica.

De schoonheid van de formule 2 sin a cos b ligt in haar eenvoud en brede toepasbaarheid. Het is een bewijs van de kracht van de wiskunde om de wereld om ons heen te beschrijven en te verklaren.

Voor- en nadelen van de 2 sin a cos b formule

Voordelen	Nadelen
Vereenvoudigt trigonometrische uitdrukkingen	Kan complex zijn om toe te passen in sommige gevallen
Helpt bij het oplossen van trigonometrische vergelijkingen	Vereist een goed begrip van trigonometrische identiteiten
Heeft brede toepassingen in verschillende vakgebieden	Kan leiden tot onnauwkeurige resultaten als het niet correct wordt toegepast

Of je nu een student bent die worstelt met trigonometrie, een professional die deze concepten in de praktijk toepast of gewoon nieuwsgierig bent naar de wiskunde die onze wereld vormgeeft, het begrijpen van de formule 2 sin a cos b opent de deur naar een wereld van mogelijkheden.