Ontdek de Kracht van Sinus, Cosinus en Tangens

26 Jun 2024
nl
Emil

Stel je voor: je staat aan de voet van een gigantische boom en je wilt weten hoe hoog hij is. Of je bent een architect die de perfecte hoek voor een dak moet berekenen. In beide gevallen komen sinus, cosinus en tangens, vaak afgekort als sin, cos en tan, te hulp! Deze drie trigonometrische functies vormen de basis voor het begrijpen van relaties tussen hoeken en zijden in rechthoekige driehoeken.

Maar hoe werken ze precies? Laten we beginnen met een rechthoekige driehoek. We kiezen een hoek anders dan de rechte hoek, bijvoorbeeld hoek A. De zijde tegenover hoek A noemen we de 'overstaande zijde'. De zijde tegenover de rechte hoek is de 'schuine zijde', en de overgebleven zijde is de 'aanliggende zijde'. Nu komen sin, cos en tan in beeld:

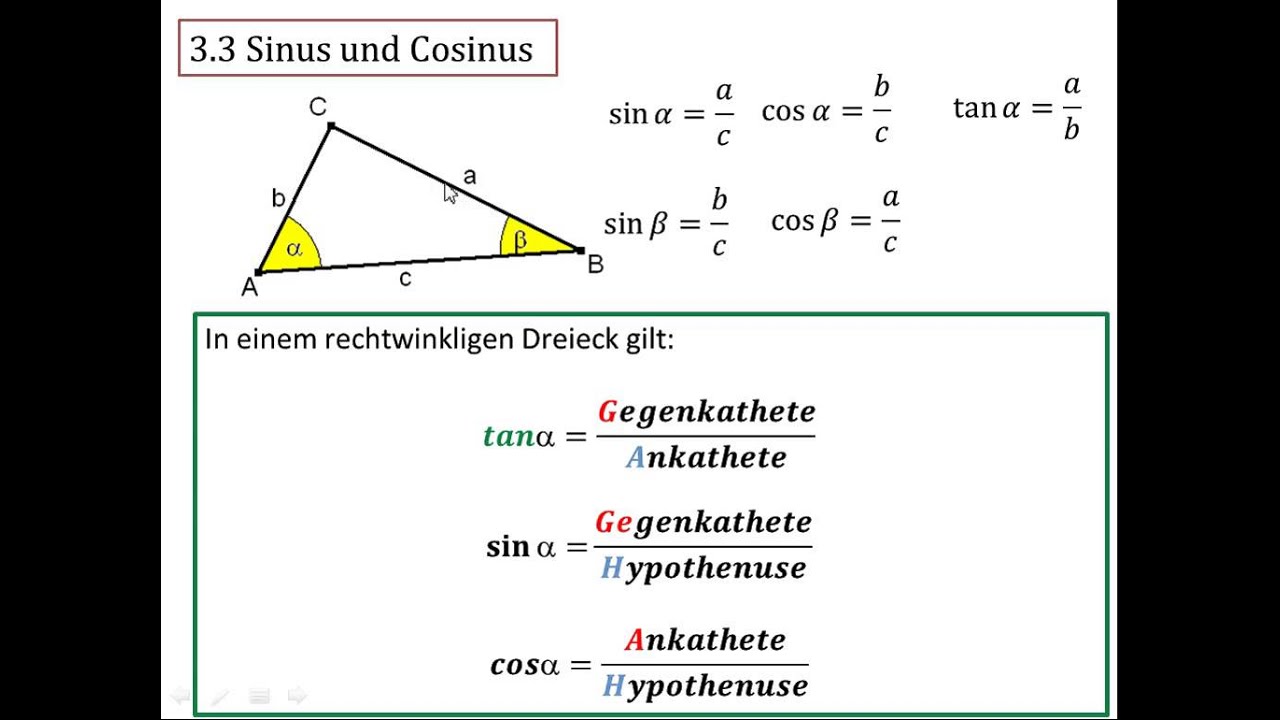
Sinus (sin): De sinus van hoek A is de verhouding tussen de lengte van de overstaande zijde en de lengte van de schuine zijde. Dus: sin A = overstaande zijde / schuine zijde.

Cosinus (cos): De cosinus van hoek A is de verhouding tussen de lengte van de aanliggende zijde en de lengte van de schuine zijde. Dus: cos A = aanliggende zijde / schuine zijde.

Tangens (tan): De tangens van hoek A is de verhouding tussen de lengte van de overstaande zijde en de lengte van de aanliggende zijde. Dus: tan A = overstaande zijde / aanliggende zijde.

Met behulp van deze formules, die je misschien nog kent uit de wiskundeles, kunnen we ontbrekende zijden of hoeken in een rechthoekige driehoek berekenen. Dit heeft talloze toepassingen in de praktijk, van navigatie en landmeting tot natuurkunde en engineering.

Denk bijvoorbeeld aan de bouw van een brug. Ingenieurs gebruiken trigonometrie om de exacte lengte en hoek van de verschillende onderdelen te berekenen, zodat de brug stevig en stabiel is. Zelfs in de medische wereld speelt trigonometrie een rol. Bij het maken van echo's worden geluidsgolven gebruikt om beelden te creëren, en trigonometrie helpt bij het bepalen van de hoek van de golven voor optimale resultaten.

Voor- en nadelen van het gebruik van Sin, Cos en Tan

Hoewel sin, cos en tan krachtige hulpmiddelen zijn, is het belangrijk om hun voor- en nadelen te begrijpen:

Voordelen	Nadelen
Nauwkeurige berekening van hoeken en zijden	Alleen toepasbaar op rechthoekige driehoeken
Breed scala aan toepassingen in verschillende vakgebieden	Vereist kennis van trigonometrische formules
Essentieel hulpmiddel voor wetenschap, techniek en meer	Kan complex zijn voor beginners

Praktische tips voor Sin, Cos en Tan

Hier zijn enkele praktische tips om sin, cos en tan effectief te gebruiken:

Onthoud de definities: Zorg ervoor dat je de definities van sinus, cosinus en tangens goed kent. Dit vormt de basis voor alle berekeningen.
Teken een schets: Teken altijd een schets van de rechthoekige driehoek en label de zijden en hoeken. Dit helpt bij het visualiseren van het probleem.
Kies de juiste formule: Bepaal welke formule (sin, cos of tan) je nodig hebt op basis van de gegeven informatie en wat je wilt berekenen.
Gebruik een rekenmachine: Gebruik een wetenschappelijke rekenmachine om de waarden van sin, cos en tan te berekenen. Zorg ervoor dat je de rekenmachine instelt op de juiste eenheid (graden of radialen).
Controleer je antwoord: Controleer altijd je antwoord door te controleren of het logisch is in de context van het probleem.

Conclusie

Sinus, cosinus en tangens zijn onmisbare hulpmiddelen voor iedereen die te maken heeft met hoeken en zijden in rechthoekige driehoeken. Van het berekenen van de hoogte van een boom tot het ontwerpen van complexe constructies, deze trigonometrische functies spelen een essentiële rol in diverse vakgebieden. Door de definities te begrijpen, te oefenen met voorbeelden en gebruik te maken van de praktische tips, kun je de kracht van sin, cos en tan benutten en een breed scala aan problemen oplossen. Dus ga aan de slag, ontdek de wereld van trigonometrie en laat je verrassen door de eindeloze mogelijkheden!