Stel je voor: je bent bezig met een DIY-project en je moet de diagonaal van een rechthoekig stuk hout berekenen. Of je bent aan het tuinieren en je wilt de optimale afstand voor je planten bepalen. In beide gevallen komt de kennis van rechthoekszijden berekenen goed van pas. Het is een essentiële wiskundige vaardigheid die je in talloze situaties kunt gebruiken.
Maar hoe pak je dat nu precies aan, het berekenen van die mysterieuze rechthoekszijde? Gelukkig is er een eeuwenoude formule die ons te hulp schiet: de stelling van Pythagoras. Deze stelling legt een elegante relatie bloot tussen de lengtes van de zijden van een rechthoekige driehoek.
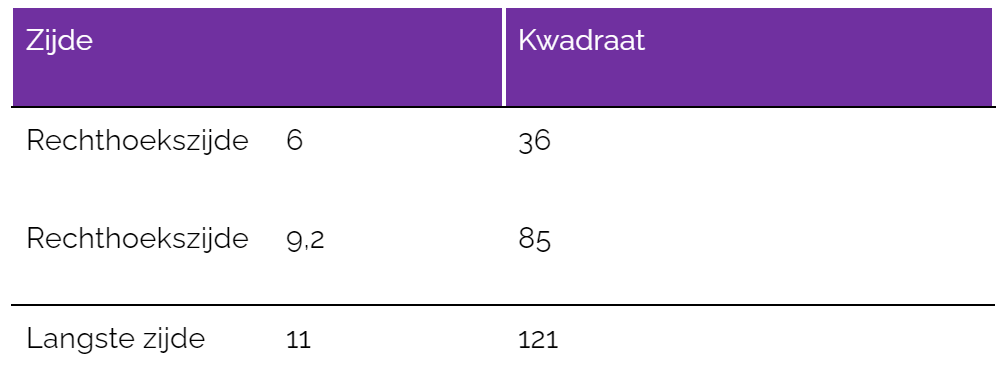
De stelling van Pythagoras stelt dat in een rechthoekige driehoek het kwadraat van de lengte van de schuine zijde (de hypotenusa) gelijk is aan de som van de kwadraten van de lengtes van de twee rechthoekszijden. In formulevorm: a² + b² = c², waarbij a en b de rechthoekszijden zijn en c de hypotenusa.
Wil je de lengte van een rechthoekszijde berekenen, dan herschrijf je de formule. Stel, je kent de lengte van de hypotenusa (c) en één rechthoekszijde (a), dan vind je de lengte van de andere rechthoekszijde (b) met de formule: b = √(c² - a²). Simpel, toch?
De stelling van Pythagoras is al eeuwenoud en wordt toegeschreven aan de Griekse wiskundige Pythagoras. Het is een fundamenteel concept in de meetkunde en heeft talloze toepassingen in de wetenschap, techniek en het dagelijks leven. Problemen die je met de stelling kunt oplossen variëren van het berekenen van afstanden tot het bepalen van de stabiliteit van constructies.
Voorbeeld: Je hebt een rechthoekige driehoek met een hypotenusa van 5 cm en een rechthoekszijde van 3 cm. De lengte van de andere rechthoekszijde bereken je als volgt: b = √(5² - 3²) = √(25 - 9) = √16 = 4 cm.
Voordelen van het beheersen van de stelling van Pythagoras:
1. Praktische toepasbaarheid: Van navigatie tot constructie, de stelling is overal bruikbaar.
2. Probleemoplossend vermogen: Je kunt complexe geometrische problemen oplossen.
3. Dieper begrip van wiskunde: Het legt de basis voor meer geavanceerde wiskundige concepten.
Stap-voor-stap handleiding:
1. Identificeer de rechthoekige driehoek.
2. Bepaal welke zijden bekend zijn (hypotenusa en/of rechthoekszijde).
3. Pas de juiste formule toe (a² + b² = c² of de afgeleide formules).
4. Bereken de onbekende zijde.
Aanbevelingen: Khan Academy biedt uitstekende online lessen over de stelling van Pythagoras.
Voor- en Nadelen
| Voordeel | Nadeel |
|---|---|
| Breed toepasbaar | Vereist accurate metingen |
Beste Praktijken:
1. Maak een schets van de driehoek.
2. Label de zijden correct.
3. Gebruik een rekenmachine voor nauwkeurige berekeningen.
4. Controleer je antwoord.
5. Oefen met verschillende voorbeelden.
Voorbeelden: (Herhaling van eerder voorbeeld + 4 extra, gebaseerd op verschillende combinaties van bekende zijden)
Uitdagingen en Oplossingen: (Voorbeelden van situaties waarin de stelling van Pythagoras moeilijk toe te passen is, zoals bij niet-perfecte rechthoekige driehoeken, en hoe deze te benaderen)
Veelgestelde Vragen: (Minimaal 8 vragen en antwoorden over de stelling van Pythagoras en het berekenen van rechthoekszijden)
Tips en Trucs: Onthoud de formule met een ezelsbruggetje.
Kortom, het berekenen van een rechthoekszijde met behulp van de stelling van Pythagoras is een krachtige tool met talloze toepassingen. Door de formule te begrijpen en te oefenen met verschillende voorbeelden, kun je deze vaardigheid effectief inzetten in diverse situaties. Of je nu bezig bent met een bouwproject, een wiskundig vraagstuk of gewoon je algemene kennis wilt vergroten, de stelling van Pythagoras is een waardevol instrument. Duik in de wereld van de meetkunde en ontdek de magie van rechthoekszijden berekenen! Deze kennis zal je ongetwijfeld van pas komen in je toekomstige ondernemingen, of het nu gaat om het ontwerpen van je droomhuis, het navigeren door de wildernis of het simpelweg oplossen van een wiskundig raadsel. De stelling van Pythagoras is meer dan alleen een formule; het is een toegangspoort tot een dieper begrip van de wereld om ons heen.
hoe bereken je een rechthoekszijde - Trees By Bike
Hoe Bereken Je Een Huurprijs - Trees By Bike
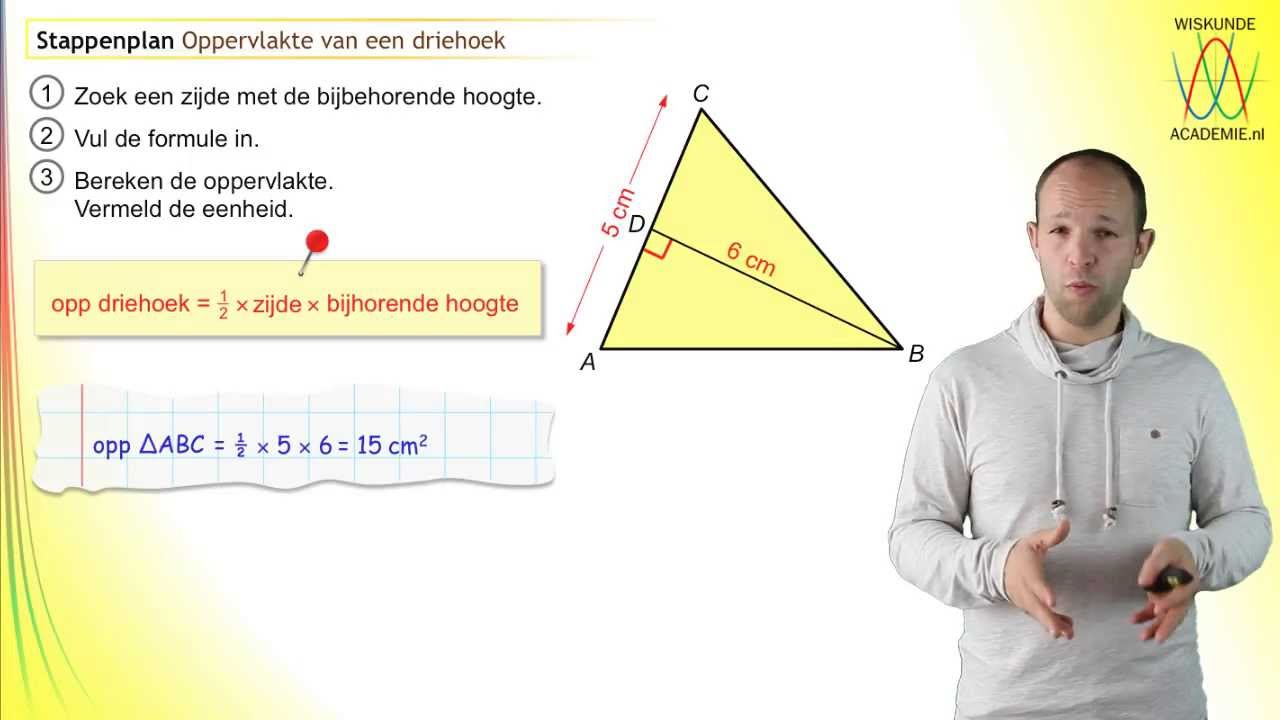
De oppervlakte van een driehoek oefenen - Trees By Bike
Hoe Bereken Je De Oppervlakte Van Een Cirkel Form - Trees By Bike
Hoe bereken je een driehoek - Trees By Bike
Hoe Bereken Je Een Vierkante Meter - Trees By Bike
Richtingscoëfficiënt berekenen oefenen - Trees By Bike
hoe bereken je een rechthoekszijde - Trees By Bike
hoe bereken je een rechthoekszijde - Trees By Bike
hoe bereken je een rechthoekszijde - Trees By Bike
Hoe Bereken Ik Een Vierkante Meter - Trees By Bike
Hoe Bereken Je De Oppervlakte Van Een Driehoek - Trees By Bike
Hoe Bereken Je Een Hoek Van Een Driehoek Een Eenvoudige Uitleg - Trees By Bike
Hoe Bereken Je De Inhoud Van Een Cilinder - Trees By Bike
LED lamp omrekenen Handige Tool Bekijk direct - Trees By Bike