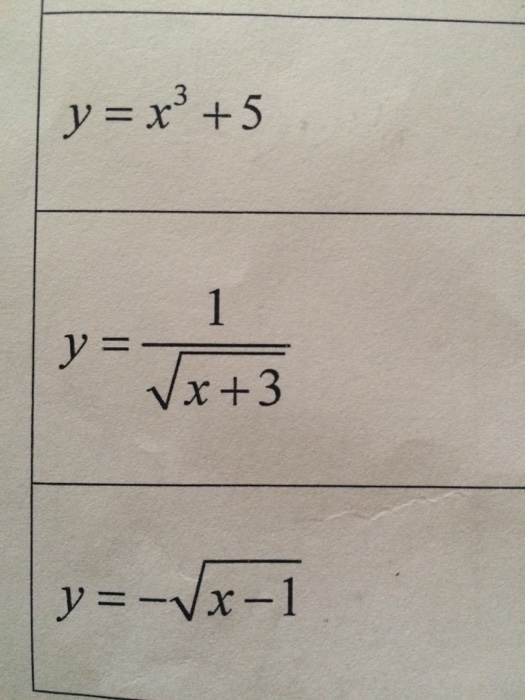Ontrafel de mysteries van x en y

19 Jul 2024
nl
Emil

find the value of x and y if x + 3 5 5 y

De zoektocht naar onbekende variabelen, zoals x en y, vormt de kern van vele wiskundige problemen. Stel je voor: x + 355y. Wat zijn x en y? Deze vraag, ogenschijnlijk simpel, opent de deur naar een fascinerende wereld van algebraïsche vergelijkingen en onthult de kracht van wiskundig redeneren.

Het vinden van de waarden van x en y in een vergelijking als x + 355y vereist meer informatie. We hebben te maken met één vergelijking met twee onbekenden, wat betekent dat er oneindig veel oplossingen mogelijk zijn. Om x en y eenduidig te bepalen, hebben we een tweede, onafhankelijke vergelijking nodig. Denk aan een schatkaart: één aanwijzing is zelden genoeg om de schat te vinden.

Laten we de vergelijking x + 355y eens nader bekijken. Zonder een tweede vergelijking kunnen we alleen de relatie tussen x en y beschrijven. We kunnen bijvoorbeeld x uitdrukken in termen van y: x = -355y. Dit betekent dat voor elke waarde die we aan y toekennen, we een corresponderende waarde voor x kunnen berekenen. Kies y = 1, dan is x = -355. Kies y = 2, dan is x = -710, enzovoort.

De geschiedenis van het oplossen van vergelijkingen met meerdere onbekenden gaat terug tot de oudheid. Babylonische kleitabletten tonen aan dat men al duizenden jaren geleden methoden ontwikkelde om dergelijke problemen aan te pakken. De ontwikkeling van de algebra, met name door Arabische wiskundigen, heeft geleid tot de systematische aanpak die we vandaag de dag gebruiken.

Het belang van het kunnen oplossen van vergelijkingen met meerdere onbekenden reikt ver buiten de wiskundeles. In de natuurkunde, economie, informatica en vele andere disciplines worden dergelijke vergelijkingen gebruikt om complexe relaties te modelleren en te analyseren. Van het berekenen van de baan van een satelliet tot het voorspellen van economische trends, de vaardigheid om x en y te vinden is essentieel.

Stel, we hebben een tweede vergelijking: 2x + y = 10. Nu kunnen we de waarden van x en y bepalen. Door substitutie of eliminatie kunnen we de twee vergelijkingen combineren om de onbekenden te isoleren en hun waarden te vinden.

Een simpel voorbeeld: als x + y = 5 en x - y = 1, dan kunnen we de twee vergelijkingen optellen om 2x = 6 te krijgen, dus x = 3. Door x = 3 te substitueren in de eerste vergelijking, vinden we y = 2.

Veelgestelde vragen:

1. Wat als ik maar één vergelijking heb? Dan zijn er oneindig veel oplossingen.

2. Hoe weet ik welke methode ik moet gebruiken? Zowel substitutie als eliminatie werken, kies de methode die het makkelijkst lijkt.

3. Kan ik grafieken gebruiken om de oplossing te vinden? Ja, het snijpunt van de grafieken van de twee vergelijkingen geeft de oplossing.

4. Wat als de vergelijkingen geen oplossing hebben? Dan zijn de lijnen parallel.

5. Wat als de vergelijkingen oneindig veel oplossingen hebben? Dan zijn de lijnen identiek.

6. Zijn er online tools die kunnen helpen? Ja, er zijn veel online rekenmachines en solvers beschikbaar.

7. Hoe kan ik mijn vaardigheden verbeteren? Oefening baart kunst! Probeer verschillende problemen op te lossen.

8. Waar kan ik meer informatie vinden? Zoek online naar "oplossen van stelsels vergelijkingen".

Tips: Oefen met verschillende soorten vergelijkingen. Controleer altijd je antwoord door de gevonden waarden terug te substitueren in de oorspronkelijke vergelijkingen.

De zoektocht naar x en y, hoe abstract ook, staat symbool voor de menselijke drang om de wereld om ons heen te begrijpen. Vanuit de fundamenten van de algebra tot de complexiteit van moderne wetenschap en technologie, het oplossen van vergelijkingen met meerdere onbekenden speelt een cruciale rol. Door te oefenen en te experimenteren met verschillende methoden, kunnen we de vaardigheid ontwikkelen om deze wiskundige puzzels op te lossen en de verborgen waarden van x en y te ontrafelen. Duik in de wereld van algebra en ontdek de schoonheid en de kracht van wiskundig redeneren. De reis naar de oplossing is net zo belangrijk als de oplossing zelf.