Stel je voor: je staat aan de voet van een majestueuze boom, de kruin reikt tot in de hemel. Hoe hoog zou deze boom zijn, vraag je je af. Of misschien ben je aan het zeilen op de eindeloze oceaan, enkel met de sterren als gids. Hoe vind je je weg over de golven, zonder te verdwalen in de uitgestrektheid? Verrassend genoeg schuilt het antwoord op beide vragen in de wondere wereld van de driehoeksmeetkunde, met name in de magische krachten van sinus, cosinus en tangens. Deze wiskundige functies, vaak afgekort tot sin, cos en tan, onthullen de geheimen van rechte driehoeken en bieden ons de sleutels tot het oplossen van talloze problemen in ons dagelijks leven.
Maar laten we eerst even terug in de tijd reizen. De wortels van de driehoeksmeetkunde reiken ver terug tot in de oudheid, waar beschavingen zoals de Babyloniërs en Egyptenaren de basis legden voor deze fascinerende tak van de wiskunde. Zij gebruikten driehoeksberekeningen voor praktische toepassingen, zoals het bepalen van landgrenzen na de overstromingen van de Nijl of het construeren van imposante piramides die de tand des tijds hebben doorstaan. De Griekse wiskundige Hipparchus van Nicea wordt vaak beschouwd als de vader van de driehoeksmeetkunde, vanwege zijn systematische studie van hoeken en de ontwikkeling van de eerste trigonometrische tabellen.
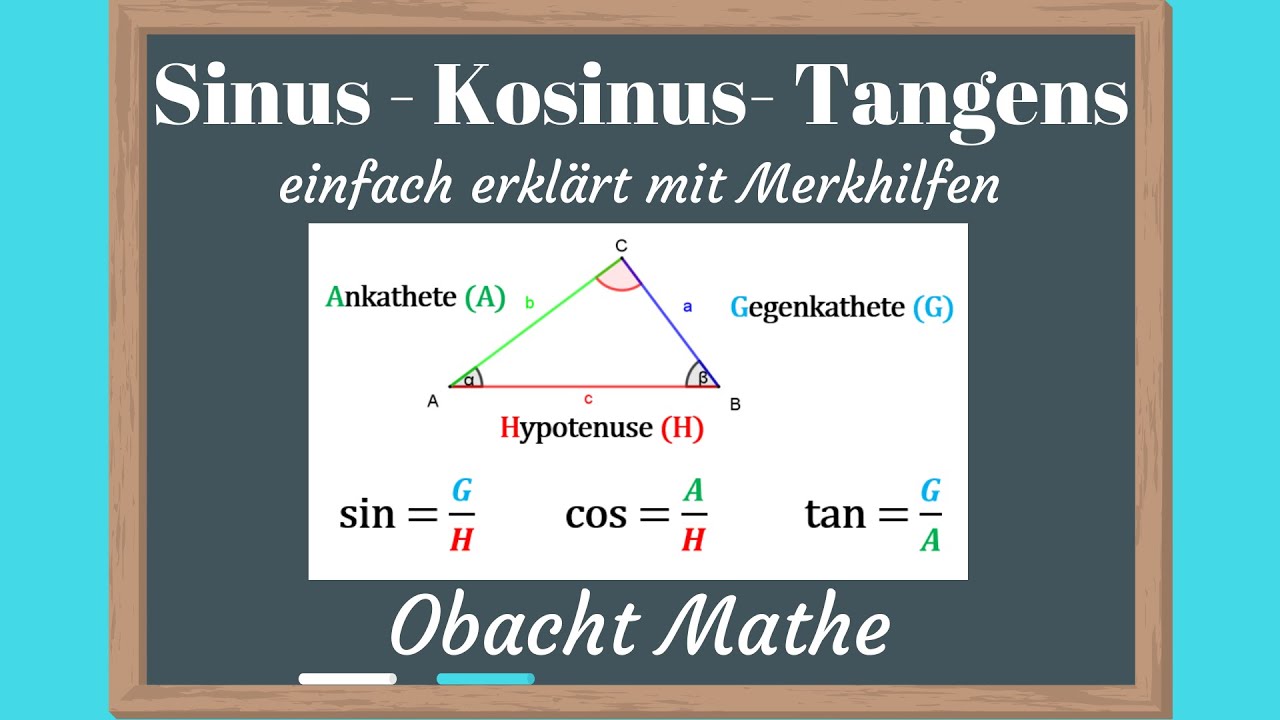
Sinus, cosinus en tangens zijn de hoekstenen van de driehoeksmeetkunde. Ze beschrijven de verhoudingen tussen de zijden van een rechte driehoek, gegeven een specifieke hoek. Simpel gezegd, de sinus van een hoek is de verhouding tussen de overstaande zijde en de schuine zijde, de cosinus is de verhouding tussen de aanliggende zijde en de schuine zijde, en de tangens is de verhouding tussen de overstaande zijde en de aanliggende zijde. Door deze verhoudingen te begrijpen en toe te passen, kunnen we ontbrekende zijden en hoeken in rechte driehoeken berekenen en daarmee een scala aan praktische problemen oplossen.
De kracht van sinus, cosinus en tangens reikt veel verder dan de klaslokalen en schoolboeken. Deze wiskundige functies vinden brede toepassing in verschillende vakgebieden, zoals bouwkunde, natuurkunde, astronomie, muziek en zelfs kunst. Architecten gebruiken ze om de stabiliteit van gebouwen te garanderen, natuurkundigen passen ze toe om de baan van projectielen te voorspellen, en astronomen gebruiken ze om de afstand tot sterren te meten. Zelfs in de muziek spelen sinusgolven een cruciale rol bij het creëren van harmonieuze klanken.
Het beheersen van sinus, cosinus en tangens opent een wereld van mogelijkheden. Het stelt ons in staat om complexe problemen te vereenvoudigen, nauwkeurige berekeningen uit te voeren en een dieper inzicht te krijgen in de wereld om ons heen. Of je nu een student bent die worstelt met wiskunde, een professional die zijn vaardigheden wil uitbreiden, of gewoon iemand die nieuwsgierig is naar de wonderen van de wiskunde, de reis door de wereld van de driehoeksmeetkunde is er een vol verrassingen en voldoening.
anwendungsaufgaben sin cos tan - Trees By Bike
anwendungsaufgaben sin cos tan - Trees By Bike
anwendungsaufgaben sin cos tan - Trees By Bike
anwendungsaufgaben sin cos tan - Trees By Bike
anwendungsaufgaben sin cos tan - Trees By Bike
Sinus Cosinus Tangens Formeln - Trees By Bike
anwendungsaufgaben sin cos tan - Trees By Bike
Sin30=? sin45=? sin60=? sin90=? sin180=? sin30=? cos30=? Cos45=? Cos60 - Trees By Bike
anwendungsaufgaben sin cos tan - Trees By Bike
Định lý hàm cosin trong tam giác và bài tập vận dụng hay nhất - Trees By Bike
Trigonometrie Erklärung mit Formeln und Beispielen - Trees By Bike
anwendungsaufgaben sin cos tan - Trees By Bike
anwendungsaufgaben sin cos tan - Trees By Bike
anwendungsaufgaben sin cos tan - Trees By Bike
anwendungsaufgaben sin cos tan - Trees By Bike