Ooit afgevraagd hoeveel liter water er in je favoriete vaas past? Of hoeveel aarde je nodig hebt voor die nieuwe bloempot? Het berekenen van inhoud, ook wel volume genoemd, is een essentiële vaardigheid die ons dagelijks leven verrijkt, van koken tot klussen. Duik met ons in de fascinerende wereld van volumeberekening en ontdek hoe je met simpele formules complexe vraagstukken kunt oplossen.
Inhoud berekenen is meer dan alleen een wiskundige oefening. Het is een praktische tool die ons helpt de wereld om ons heen te begrijpen en te manipuleren. Stel je voor dat je een zwembad vult: zonder kennis van volumeberekening zou je eindeloos water kunnen blijven toevoegen! Of denk aan het bakken van een taart: de juiste hoeveelheden ingrediënten zijn cruciaal voor een perfect resultaat. In feite gebruiken we de principes van volumeberekening constant, vaak zonder erbij stil te staan.
De geschiedenis van volumeberekening gaat ver terug. Al in de oudheid worstelden wiskundigen met het bepalen van de inhoud van verschillende vormen. Van de piramides van Egypte tot de amforen van Griekenland, de behoefte om inhoud te meten was alomtegenwoordig. Archimedes, een briljante Griekse wetenschapper, maakte baanbrekende ontdekkingen op dit gebied, waaronder de beroemde wet van Archimedes die de opwaartse kracht op een voorwerp in een vloeistof beschrijft.
Het belang van inhoud berekenen reikt verder dan dagelijkse toepassingen. In de wetenschap, techniek en architectuur speelt volumeberekening een cruciale rol. Denk aan het ontwerpen van een vliegtuig, het bouwen van een brug of het ontwikkelen van nieuwe medicijnen. Zonder een grondig begrip van volume en hoe dit te berekenen, zouden deze complexe projecten onmogelijk zijn.
Het berekenen van inhoud kan echter ook uitdagingen met zich meebrengen, vooral bij onregelmatige vormen. Gelukkig bestaan er verschillende methoden en formules om deze problemen te overwinnen. Van eenvoudige formules voor kubussen en balken tot meer complexe integraalrekening voor onregelmatige vormen, er is altijd een geschikte aanpak te vinden.
Voor een kubus bereken je de inhoud door lengte x breedte x hoogte. Voor een bol is de formule (4/3)πr³, waarbij r de straal is. Een cilinder? πr²h, waarbij h de hoogte is. Eenvoudig, toch?
Drie voordelen van het beheersen van inhoud berekenen zijn: 1. Nauwkeurige metingen voor kook- en bakrecepten. 2. Efficiënt inpakken en verhuizen door de juiste doosgroottes te kiezen. 3. Kostenbesparing door de juiste hoeveelheid materiaal te kopen voor DIY-projecten.
Een actieplan: 1. Identificeer de vorm. 2. Kies de juiste formule. 3. Voer de metingen in. 4. Bereken de inhoud.
Voor- en Nadelen van Inhoud Berekenen
| Voordeel | Nadeel |
|---|---|
| Nauwkeurige metingen | Complexe formules voor onregelmatige vormen |
Vijf beste praktijken: 1. Gebruik de juiste eenheden. 2. Controleer je metingen. 3. Gebruik een rekenmachine. 4. Rond af op het juiste aantal significante cijfers. 5. Oefen regelmatig.
Vijf voorbeelden: 1. Inhoud van een zwembad. 2. Inhoud van een theekopje. 3. Inhoud van een schoenendoos. 4. Inhoud van een ballon. 5. Inhoud van een aquarium.
Vijf uitdagingen en oplossingen: 1. Onregelmatige vormen: gebruik benaderingsmethoden. 2. Complexe formules: gebruik een rekenmachine of software. 3. Onnauwkeurige metingen: meet zorgvuldig. 4. Verkeerde eenheden: converteer naar de juiste eenheden. 5. Gebrek aan oefening: oefen regelmatig.
FAQ: 1. Wat is inhoud? 2. Hoe bereken je de inhoud van een kubus? 3. Wat is de formule voor de inhoud van een bol? 4. Hoe meet je de straal van een cirkel? 5. Wat zijn de eenheden voor inhoud? 6. Hoe converteer je tussen verschillende eenheden? 7. Waar kan ik meer informatie vinden over inhoud berekenen? 8. Wat zijn enkele veelvoorkomende fouten bij het berekenen van inhoud?
Tips en trucs: Gebruik een meetlint voor nauwkeurige metingen. Oefen met verschillende vormen. Visualiseer de vorm in 3D.
Kortom, het berekenen van inhoud is een essentiële vaardigheid die ons in staat stelt de wereld om ons heen te begrijpen en te beïnvloeden. Van het bakken van een taart tot het ontwerpen van een wolkenkrabber, de toepassingen zijn eindeloos. Hoewel het soms uitdagend kan zijn, bieden de beschikbare formules en methoden ons de tools om elk volumeprobleem aan te pakken. Door te oefenen en te experimenteren, kunnen we de magie van inhoud berekenen ontsluiten en onze kennis toepassen in talloze situaties. Dus, de volgende keer dat je je afvraagt hoeveel er in die pot past, grijp dan naar je meetlint en reken het uit! Je zult versteld staan van de kracht van deze eenvoudige, maar essentiële vaardigheid.
Hoe Bereken Je Het Gemiddeld Eigen Vermogen - Trees By Bike
hoe reken je inhoud uit - Trees By Bike
Nieuwe formule zo reken je uit hoe oud je hond is in mensenjaren - Trees By Bike
hoe reken je inhoud uit - Trees By Bike
Werkblad Hoeveel is het samen 2 - Trees By Bike
hoe reken je inhoud uit - Trees By Bike
hoe reken je inhoud uit - Trees By Bike
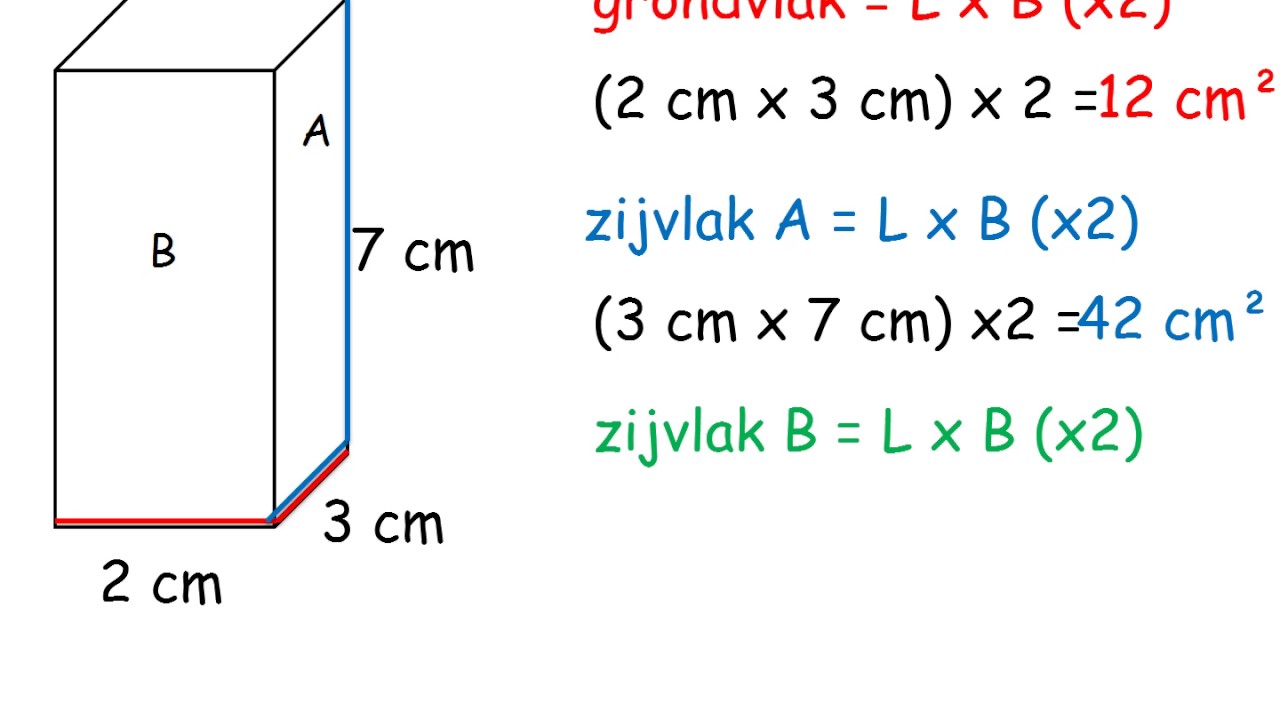
Inhoud balk en kubus - Trees By Bike
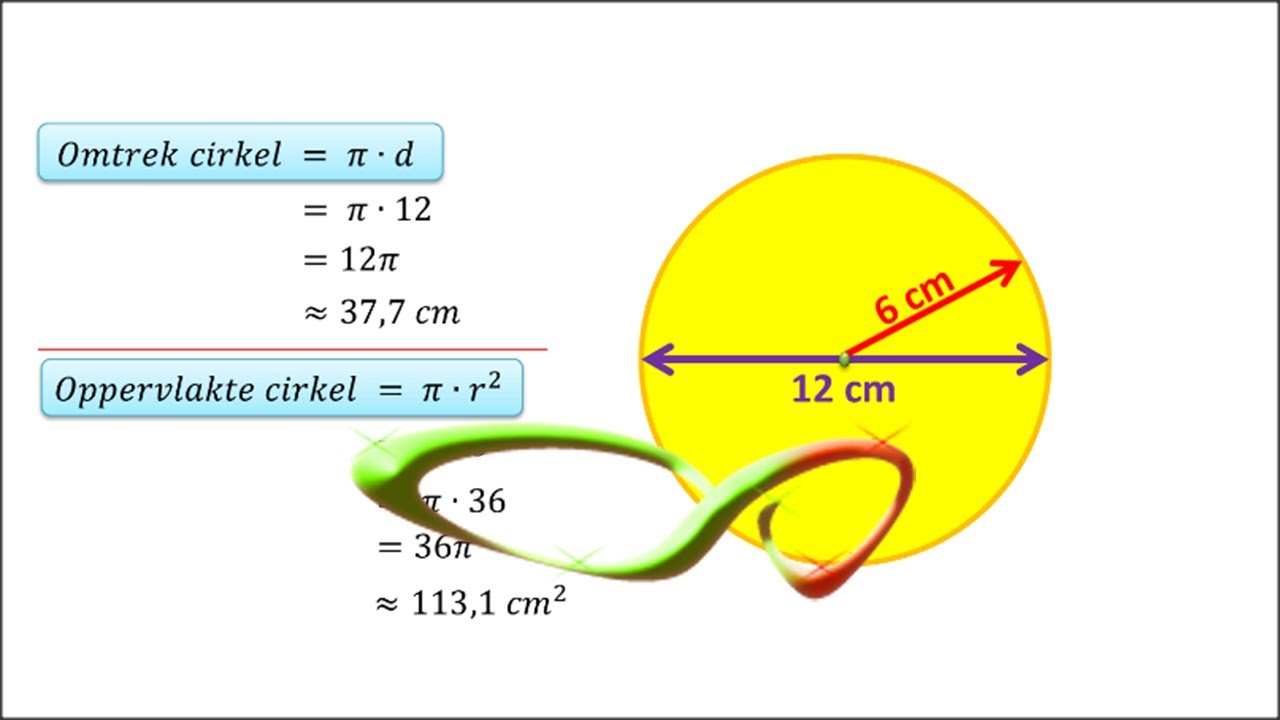
Scholierencom Videoplatform Omtrek en oppervlakte van een cirkel - Trees By Bike
Hoe Reken Je M3 Uit Eenvoudige Tips Voor Berekeningen - Trees By Bike
Kapitän Erschöpfung Lindern meter naar kubieke meter Lieber Besetzen - Trees By Bike
hoe reken je inhoud uit - Trees By Bike
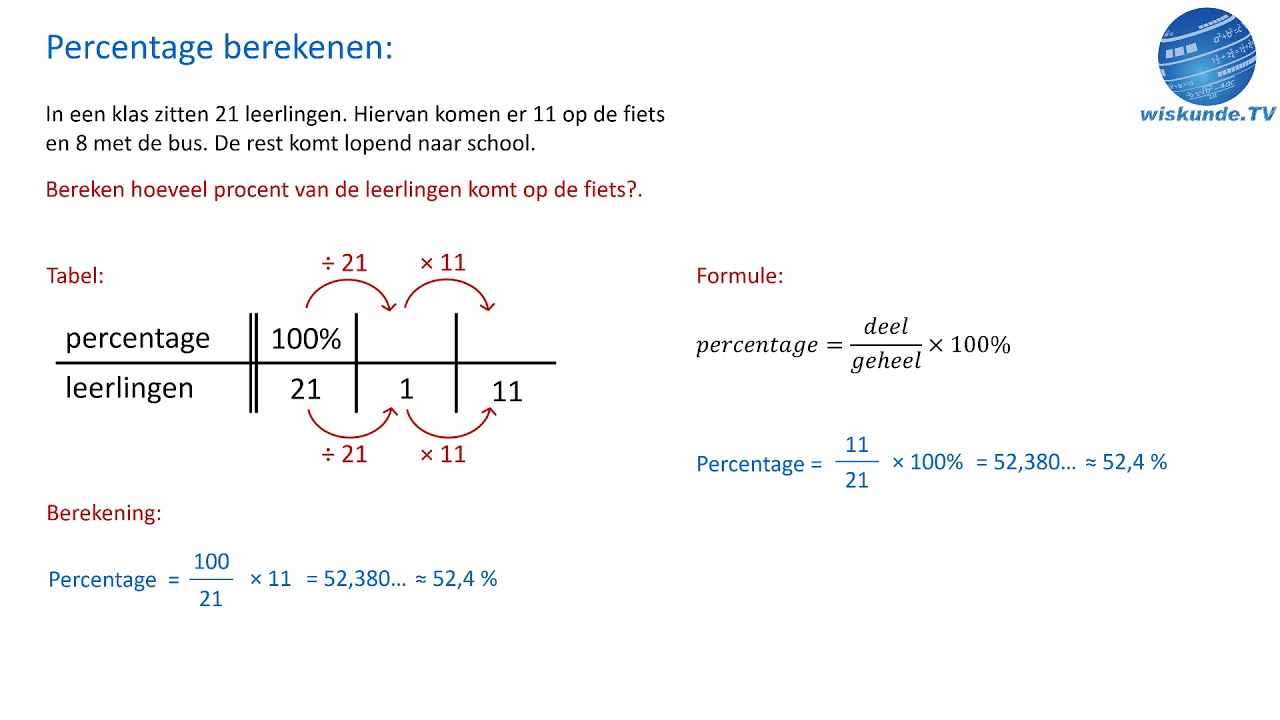
Hoe reken je procenten uit - Trees By Bike
Hier ziet u een voorbeeld hoe het beste verhaaltjes sommen moeten - Trees By Bike
Omtrek en oppervlakte van vlakke figuren Formules - Trees By Bike