Cracking Geometry's Code: The 3 Undefined Terms You Need to Know

09 May 2024
us
Emil

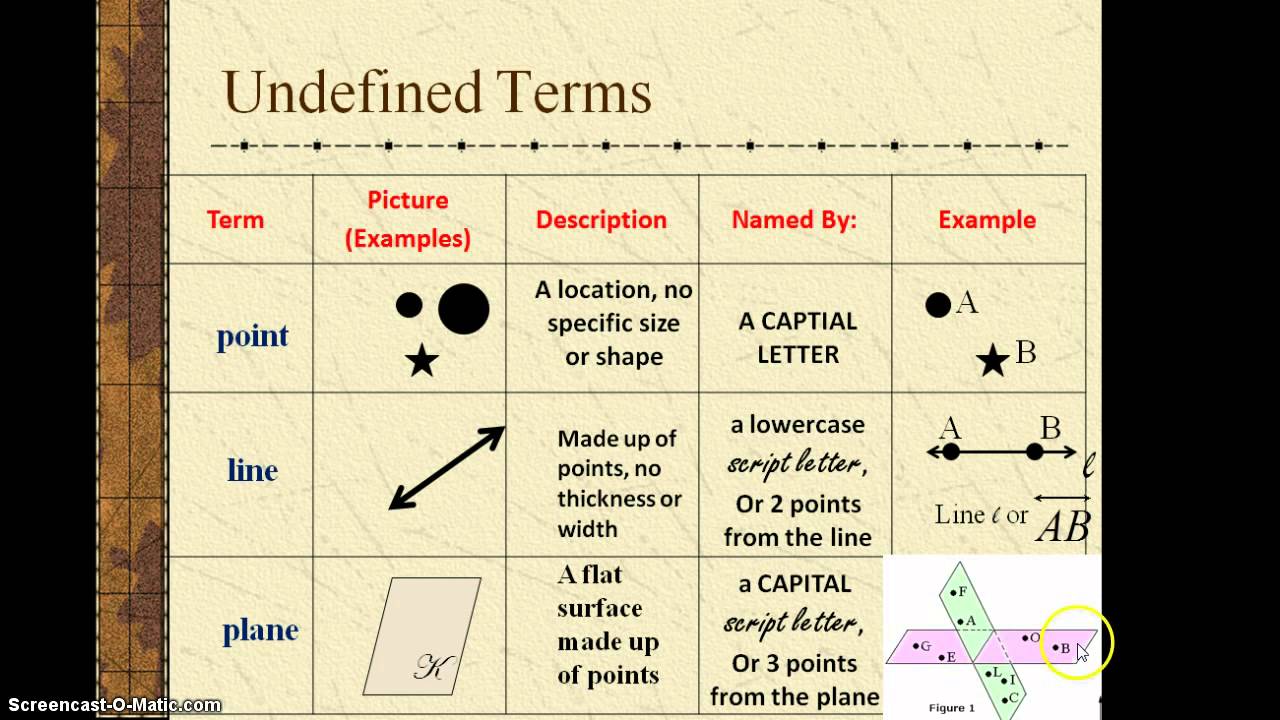
Have you ever wondered how mathematicians build complex geometric structures? Like a magnificent skyscraper that rises from a simple foundation, the entire edifice of geometry rests upon three fundamental concepts. These are not complex formulas or intricate theorems, but rather, intriguingly, undefined terms: the point, the line, and the plane.

These terms might seem deceptively simple, almost self-evident. After all, we intuitively grasp what a point, a line, or a plane represents. We see dots, lines, and flat surfaces every day. Yet, attempting to define them precisely, using only words, proves to be a surprisingly difficult task. This is where the fascinating interplay of intuition and rigorous logic comes into play in geometry.

The challenge in defining these basic elements arises from the need to avoid circularity. Any definition we provide for one of these terms would inevitably rely on other terms that themselves require definition. For instance, how would you define a line without mentioning points, or a plane without referring to lines or points? It becomes a linguistic merry-go-round.

To escape this circularity, mathematicians have ingeniously chosen to leave these three fundamental concepts undefined. Instead of getting bogged down in verbal definitions, they focus on establishing relationships between these terms through axioms or postulates. These axioms serve as the bedrock upon which the entire structure of geometric theorems and proofs is built.

While we may not be able to pin down these terms with precise verbal definitions, we can certainly understand them intuitively and describe their properties. A point, for example, can be thought of as a location in space, having no size or dimension. A line can be visualized as a straight path that extends infinitely in both directions, possessing only length but no width or height. A plane, then, extends infinitely in two dimensions, like an infinitely large, perfectly flat sheet of paper.

This approach of starting with undefined terms might seem counterintuitive at first, but it highlights a fundamental aspect of mathematics: the reliance on clear, unambiguous concepts as building blocks for more complex ideas. The undefined terms in geometry form the foundation upon which a vast and intricate mathematical framework is constructed. By carefully defining the relationships between these basic elements, mathematicians have developed a powerful tool for understanding and describing the world around us.

Advantages and Disadvantages of Using Undefined Terms in Geometry

Advantages	Disadvantages
Provides a clear and unambiguous foundation for geometry.	Can be counterintuitive for learners at first.
Avoids circular definitions and logical inconsistencies.	Requires reliance on axioms and postulates, which themselves may be abstract.
Allows for the development of a rigorous and logically sound system of geometry.	May make it challenging to connect abstract geometric concepts to real-world applications initially.

Common Questions and Answers about the Undefined Terms in Geometry

1. Why are these terms left undefined?

Leaving them undefined prevents circular definitions and provides a solid, unambiguous foundation for geometry.

2. Can we think of points, lines, and planes as real-world objects?

While we use real-world examples to visualize them, points, lines, and planes are abstract concepts. They are tools for modeling and understanding the world but don't perfectly represent physical objects.

3. How are the undefined terms used to define other geometric concepts?

Other geometric terms, like angles, shapes, and solids, are defined using the relationships and properties established between points, lines, and planes through axioms and postulates.

4. What is an example of an axiom related to these terms?

One famous axiom is "Two points determine a unique line." This simple statement establishes a fundamental relationship between points and lines.

5. What is the significance of undefined terms in mathematics beyond geometry?

The idea of using undefined terms to build a system of logic extends to other areas of mathematics. It highlights how mathematicians create rigorous systems by carefully defining relationships between fundamental concepts.

6. Are there other geometries where these terms are defined?

In some non-Euclidean geometries, the concepts of lines and planes might have different properties or interpretations than in the standard Euclidean geometry we learn in school.

7. How do these undefined terms help in problem-solving?

By understanding the properties and relationships between points, lines, and planes, we can use geometric reasoning to solve problems related to spatial relationships, measurements, and constructions.

8. What is the historical context of using undefined terms in geometry?

Euclid's "Elements," written over 2000 years ago, is one of the earliest examples of a mathematical system built on undefined terms and axioms. This approach has been influential in shaping the development of mathematics throughout history.

Understanding the undefined terms in geometry is not just an academic exercise; it is about grasping the fundamental building blocks of a system that helps us describe and analyze the world around us. These seemingly simple concepts, with their carefully defined relationships, underpin a vast and powerful field of mathematics that has applications in art, architecture, engineering, and countless other areas. So, the next time you see a dot on a page, a straight line drawn on a map, or a flat surface, remember that you are witnessing the manifestations of the fundamental, yet undefined, building blocks of geometry.