Ever wondered how AC circuits manage to function with those quirky components like inductors? It's a world of oscillating currents and voltages, a dance of electrons that's far more complex than the steady direct current realm. At the heart of understanding this intricate dance lies the concept of the inductor's phasor representation.
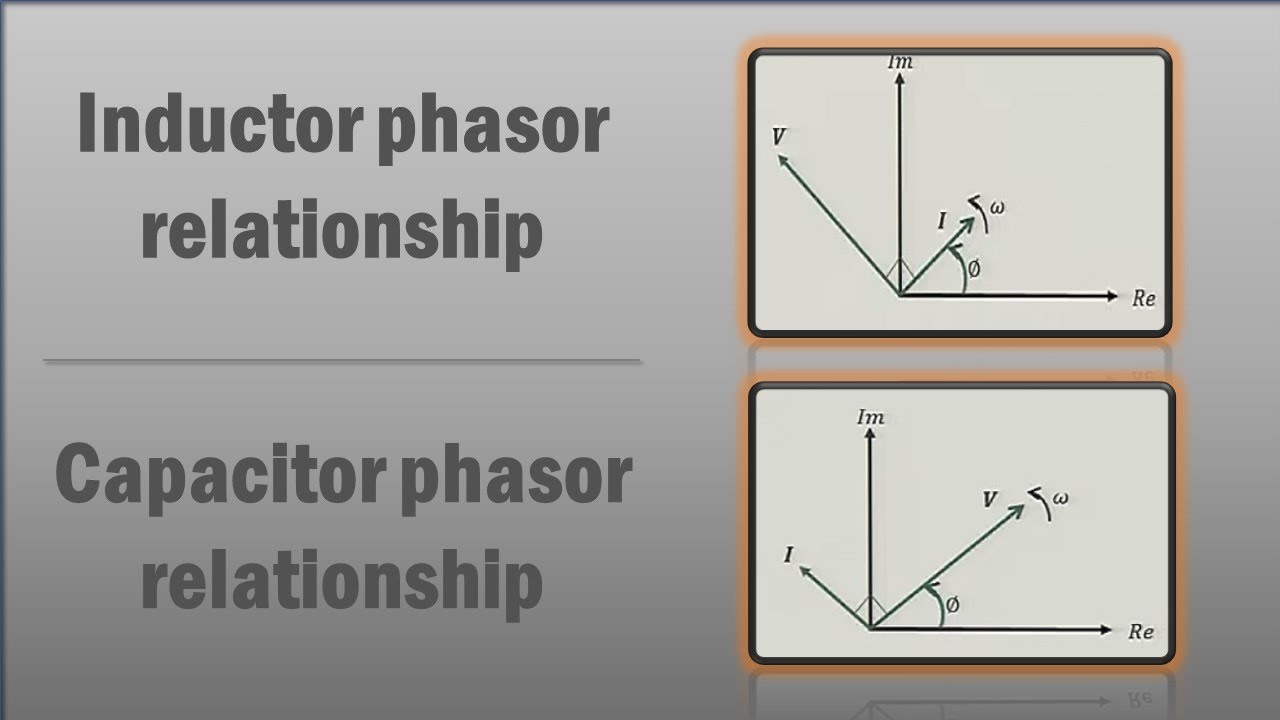
Imagine trying to analyze a circuit where the voltage and current are constantly changing direction. Sounds like a nightmare, right? That's where phasors come to the rescue. They're like mathematical superheroes, transforming these oscillating signals into static vectors, making analysis much simpler. The phasor of an inductor is a key to unlocking the secrets of its behavior in AC circuits.
An inductor, essentially a coil of wire, stores energy in its magnetic field when current flows through it. This stored energy then resists changes in the current, making the inductor behave differently in AC circuits compared to DC circuits. In a DC circuit, an inductor eventually acts like a short circuit once the magnetic field is established. But in an AC circuit, the constantly changing current means the magnetic field is also constantly changing, leading to a continuous opposition to the current flow. This opposition is represented by inductive reactance.
The phasor representation of an inductor helps us visualize this opposition. The inductor phasor is drawn 90 degrees ahead of the current phasor. This 90-degree phase shift reflects the fact that the voltage across the inductor leads the current through it. The magnitude of the inductor phasor represents the inductive reactance, which depends on the frequency of the AC signal and the inductance of the coil. Understanding the inductor's phasor is fundamental to analyzing any AC circuit containing an inductor.
Historically, the concept of phasors emerged as a tool to simplify AC circuit analysis. Before phasors, engineers relied on complex differential equations to describe the behavior of AC circuits. Phasors provided a much more intuitive and manageable way to deal with these oscillating signals. The ability to represent sinusoidal quantities as vectors greatly simplified the process of calculating circuit parameters like impedance and current.
The importance of understanding the phasor representation of an inductor cannot be overstated. It’s essential for designing and analyzing a wide range of circuits, from simple filters to complex power systems. Misunderstanding or neglecting the inductor's phasor behavior can lead to incorrect circuit designs, unexpected performance, or even component failure.
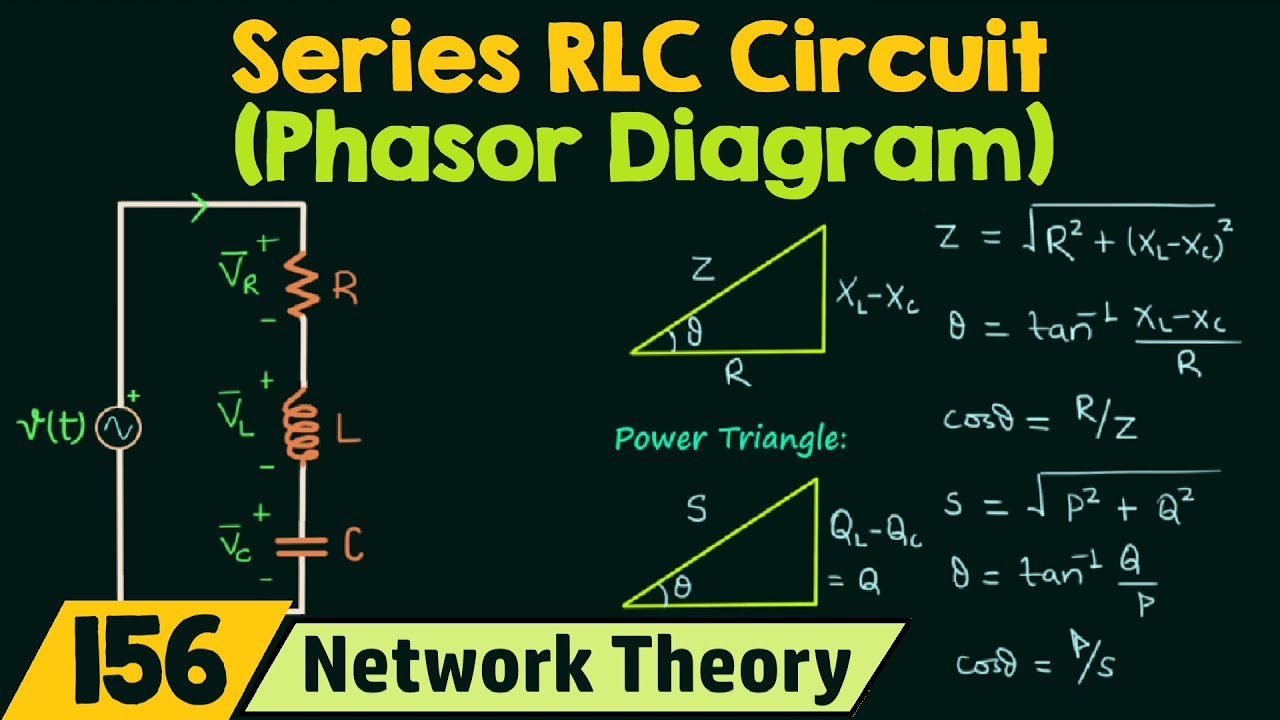
For instance, in resonance circuits, the interplay between inductive and capacitive reactance is crucial. The phasor diagram helps visualize how these reactances cancel each other out at the resonant frequency. This principle is fundamental in applications like radio tuning, where selecting a specific frequency is essential.
A practical example of inductor phasor utilization is in power factor correction. Industrial loads often have a lagging power factor due to inductive components like motors. This leads to inefficient power transmission. By adding capacitors, which have a leading power factor, the overall power factor can be improved, bringing it closer to unity. Phasor diagrams are used to calculate the required capacitance for effective power factor correction.
Advantages and Disadvantages of using Phasor Representation for Inductors
| Advantages | Disadvantages |
|---|---|
| Simplifies AC circuit analysis | Only applicable to sinusoidal signals |
| Provides a visual representation of circuit behavior | Can be initially challenging to grasp |
| Facilitates calculations of impedance and current | Doesn't directly represent transient behavior |
While phasor diagrams don't show transient behavior, they offer crucial insights into the steady-state AC behavior of inductors, simplifying a complex topic considerably. Without the concept of the inductor's phasor, designing and analyzing AC circuits would be significantly more challenging.
One of the biggest challenges with inductive circuits is dealing with inductive spikes, which can damage components. Understanding the phasor representation and how inductors react to sudden changes in current is key to mitigating these risks. Utilizing techniques like snubber circuits can help suppress these voltage spikes.
Frequently Asked Questions about inductors and phasors:
1. What is a phasor? (A: A complex number representing a sinusoidal function.)
2. What is inductive reactance? (A: The opposition to current flow in an inductor in an AC circuit.)
3. How does the inductor phasor relate to current? (A: It leads the current phasor by 90 degrees.)
4. Why do we use phasors? (A: To simplify AC circuit analysis.)
5. What is the importance of inductor phasor in power factor correction? (A: It helps determine the required capacitance for correction.)
6. How does frequency affect the inductor phasor? (A: Higher frequency leads to higher inductive reactance and a larger phasor magnitude.)
7. What are some common applications of inductors in AC circuits? (A: Filters, transformers, motors.)
8. How can I visualize the relationship between voltage and current in an inductive circuit using phasors? (A: Draw the voltage phasor 90 degrees ahead of the current phasor.)
In conclusion, understanding the inductor's phasor representation is essential for anyone working with AC circuits. From simplifying complex calculations to enabling the design of crucial electronic systems, the phasor concept empowers us to tame the wild oscillations of alternating current and harness the unique properties of inductors. By grasping the fundamentals of phasors and their relationship to inductors, we unlock the potential to design innovative circuits and systems that shape our modern world. Continue exploring the fascinating world of AC circuit analysis and the power of phasors. There are numerous resources available online, including educational websites, tutorials, and simulation tools. Your journey into the world of electronics starts here! Delve deeper, experiment, and discover the endless possibilities that await.
For a purely inductive ac circuit show that the current lags the - Trees By Bike
inductor of a phasor - Trees By Bike
What is a phasor diagram - Trees By Bike
Equivalent Circuit Diagram Of Induction Motor - Trees By Bike
Phasor Diagram Of Inductor And Capacitor - Trees By Bike
What Is The Symbol For Inductive Reactance at Graham Odell blog - Trees By Bike
Phasor Diagram For Inductive Circuit - Trees By Bike
How To Draw Phasor Diagram at How To Draw - Trees By Bike
Pure Inductive Circuit Phasor Diagram - Trees By Bike
An Inductor L And Resistance R Are Connected In Series at Carolyn - Trees By Bike
Phasor Diagram For Inductive Circuit - Trees By Bike
Phasor Diagram For Inductive Circuit - Trees By Bike
AC supply to pure inductor theory phasor waveforms - Trees By Bike
Phasor Diagram Of Inductor In Ac Circuit - Trees By Bike
Ac Circuit Phasor Diagram Impedance - Trees By Bike