The Unshakeable Foundations: What Are Undefined Terms in Geometry?

01 Aug 2024
us
Emil

Imagine trying to build a house without first laying a strong foundation. Chaos would ensue, right? The walls might tilt, the roof could cave in – the whole structure would be compromised. In the realm of geometry, we encounter a similar situation. Before we can delve into the world of angles, lines, and shapes, we need a solid groundwork. This is where undefined terms come in, acting as the invisible bedrock upon which the entire edifice of geometric reasoning is built.

But how can something be undefined yet fundamental? It seems paradoxical. In our quest to make sense of the world, we strive for clear-cut definitions. Yet, some concepts are so basic, so elemental, that any attempt to define them would require using other terms that themselves rely on the very concept we’re trying to define. It becomes a circular chase, a linguistic merry-go-round. And that’s where the beauty of undefined terms lies.

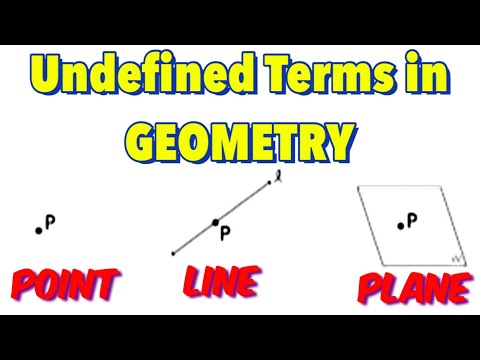
These terms, while lacking strict definitions, are imbued with intuitive understanding. We accept them as self-evident truths, as the building blocks upon which we construct more complex geometric ideas. Think of a point, a location in space with no size or dimension. We can’t really define it, yet we instinctively grasp the concept. The same goes for a line, extending infinitely in both directions, or a plane, a flat surface stretching endlessly in all directions.

These undefined terms, namely point, line, and plane, form the bedrock of Euclidean geometry, the system developed by the Greek mathematician Euclid in the 3rd century BC. Euclid’s genius lay in recognizing that starting with these simple, undefined notions, he could logically deduce a vast array of geometric theorems and relationships.

The undefined terms, far from being weaknesses, are the very strength of geometry. Their lack of rigid definitions allows for flexibility and broad applicability. They provide a common starting point, a universal language that transcends cultural and linguistic barriers. A point is a point, whether you’re in ancient Greece, modern-day Tokyo, or a galaxy far, far away.

Advantages and Disadvantages of Undefined Terms in Geometry

Advantages	Disadvantages
Provide a foundation for defining other geometric terms.	Can lead to ambiguity if not used carefully.
Allow for flexibility in interpreting and applying geometric concepts.	Can make it challenging to prove certain geometric theorems rigorously.
Facilitate communication and understanding across cultures and languages.

Common Questions and Answers About Undefined Terms in Geometry

1. Why are undefined terms necessary in geometry?

Undefined terms are necessary to avoid circular definitions and provide a common starting point for building geometric concepts.

2. What are some other examples of undefined terms in mathematics?

In set theory, the concept of a "set" itself is undefined. In logic, "true" and "false" are considered undefined primitives.

3. Can undefined terms be visualized?

While we can use diagrams and representations to aid our understanding, it's important to remember that these are just representations. The undefined terms themselves are abstract concepts.

4. Do undefined terms have any real-world applications?

Even though they are abstract, undefined terms form the basis for the geometry used in fields like architecture, engineering, computer graphics, and physics.

5. Are undefined terms the same across all geometries?

Different geometries, like non-Euclidean geometries, may have slightly different undefined terms or interpretations of these terms.

6. How do undefined terms impact our daily lives?

From the layout of cities to the design of everyday objects, the principles of geometry, rooted in undefined terms, shape our world in countless ways.

7. Can we ever fully define undefined terms?

It's unlikely. The beauty and power of these terms lie in their simplicity and the foundation they provide for building a complex and elegant system of geometric reasoning.

8. How can I better understand undefined terms in geometry?

Explore geometry textbooks, online resources, or engage with math enthusiasts to deepen your understanding of these fundamental concepts.

In the grand tapestry of mathematics, undefined terms are the threads, seemingly simple yet essential, that hold everything together. They remind us that even in our quest for precise definitions, some concepts are best understood through intuition and their relationship to other ideas. Just like a house needs a strong foundation to stand the test of time, so too does geometry rely on its undefined terms to support the weight of its profound theorems and elegant proofs. These terms, in their undefined glory, underpin the very fabric of our spatial reasoning and shape our understanding of the world around us. So, the next time you ponder a geometric problem, take a moment to appreciate the silent power of those undefined terms—the unsung heroes of the geometric world.