Have you ever wondered how to make sense of a bunch of numbers? Maybe you're looking at your monthly expenses, tracking your running times, or trying to understand your grades. One powerful tool for making sense of data is the average, sometimes called the mean. Don't let the mathematical term scare you – it's a simple concept that can be incredibly useful in everyday life.
In its simplest form, an average tells you the central tendency of a set of numbers. Imagine you have a group of friends, and you want to know the average height of the group. By adding up everyone's height and then dividing by the number of people, you get the average height. This single number gives you a general idea of how tall the group is overall.
The concept of the average has been used for centuries, dating back to ancient civilizations who used it for tasks like dividing land and tracking harvests. Today, averages are everywhere, from calculating sports statistics to analyzing financial markets. They help us understand trends, make comparisons, and draw meaningful conclusions from data.
One of the main issues with averages is that they can be influenced by outliers, which are extreme values that are significantly higher or lower than the other values in the data set. For example, if you're calculating the average income of a group of people, and one person in the group earns significantly more than everyone else, that person's income will skew the average upwards, making it seem like the average income is higher than it actually is for most people in the group.
To calculate the average, or mean, of a set of numbers, you simply add up all the numbers in the set and then divide by the total number of values in the set. For example, let's say you want to find the average of the following numbers: 5, 10, 15, and 20. First, add up all the numbers: 5 + 10 + 15 + 20 = 50. Then, divide the sum (50) by the total number of values (4): 50 / 4 = 12.5. Therefore, the average of the numbers 5, 10, 15, and 20 is 12.5.
Advantages and Disadvantages of Using Averages
| Advantages | Disadvantages |
|---|---|
| Simple to calculate and understand | Can be affected by outliers (extreme values) |
| Provides a single representative value for a data set | May not accurately represent the typical value in skewed distributions |
| Useful for making comparisons between different data sets | Does not provide information about the spread or variability of the data |
While averages are useful, it's important to remember that they only tell part of the story. Looking at the range of values, the distribution of the data, and other statistical measures can provide a more complete understanding of the information you're analyzing.
In conclusion, understanding averages is essential for navigating a world filled with data. Whether you're deciphering statistics in the news, making informed decisions in your personal life, or excelling in your academic pursuits, the ability to calculate and interpret averages is a valuable skill that empowers you to make sense of the world around you.
Solved: 20. The diagram shows the distance - Trees By Bike
Jawapan Formula A+ Geografi Tingkatan 3 - Trees By Bike
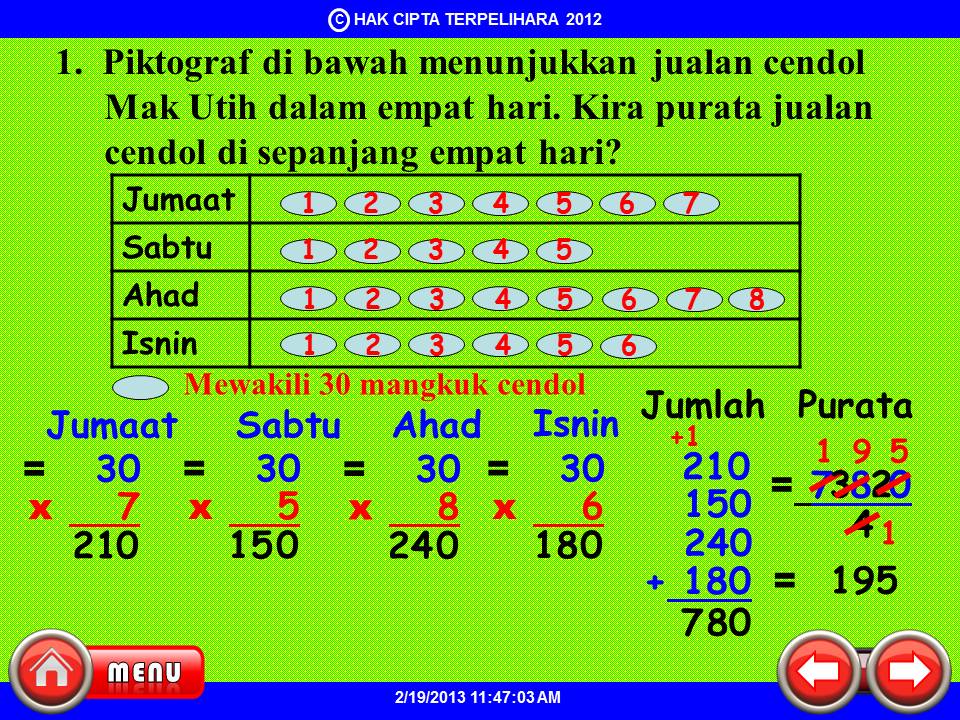
cara kira purata min - Trees By Bike
Mean, Median, dan Modus Data Kelompok Beserta Soal dan Pembahasannya - Trees By Bike
cara kira purata min - Trees By Bike
cara kira purata min - Trees By Bike
cara kira purata min - Trees By Bike
cara kira purata min - Trees By Bike
cara kira purata min - Trees By Bike
cara kira purata min - Trees By Bike
cara kira purata min - Trees By Bike