Ever stared at a complex AC circuit and felt a wave of confusion wash over you? Resistors, capacitors, inductors... all buzzing with sinusoidal voltages and currents, shifting and changing over time. It's like trying to juggle jellyfish. Thankfully, there's a powerful tool that simplifies AC circuit analysis: phasor domain calculations. This is your gateway to understanding the magic behind those oscillating voltages and currents.
Imagine trying to describe the swirling motion of a Ferris wheel by tracking each individual cabin’s up-and-down movement over time. Tedious, right? Phasors offer a similar simplification for AC circuits. Instead of grappling with time-varying sinusoidal functions, we represent voltages and currents as rotating vectors, called phasors, making analysis much more manageable.
Calculating phasor domain voltages is essential for electrical engineers, anyone working with electronics, or even DIY enthusiasts dabbling with AC circuits. It unlocks the ability to predict and control the behavior of these circuits, paving the way for designing everything from power systems to intricate electronic devices. Without phasors, the world of AC circuits would remain a bewildering maze of oscillating signals.
The concept of phasors arose from the need to simplify the mathematical analysis of AC circuits. Early electrical engineers wrestled with complex differential equations to understand these circuits. Charles Proteus Steinmetz, a brilliant mathematician and electrical engineer, pioneered the use of phasors in the late 19th century. This innovation revolutionized AC circuit analysis, transforming a complex problem into a more manageable one.
One of the main issues addressed by phasor domain calculations is the difficulty of performing arithmetic operations on sinusoidal functions. Adding or subtracting sinusoids with different phases is a tedious trigonometric exercise. Phasors transform these trigonometric operations into simpler vector operations, significantly streamlining the analysis process.
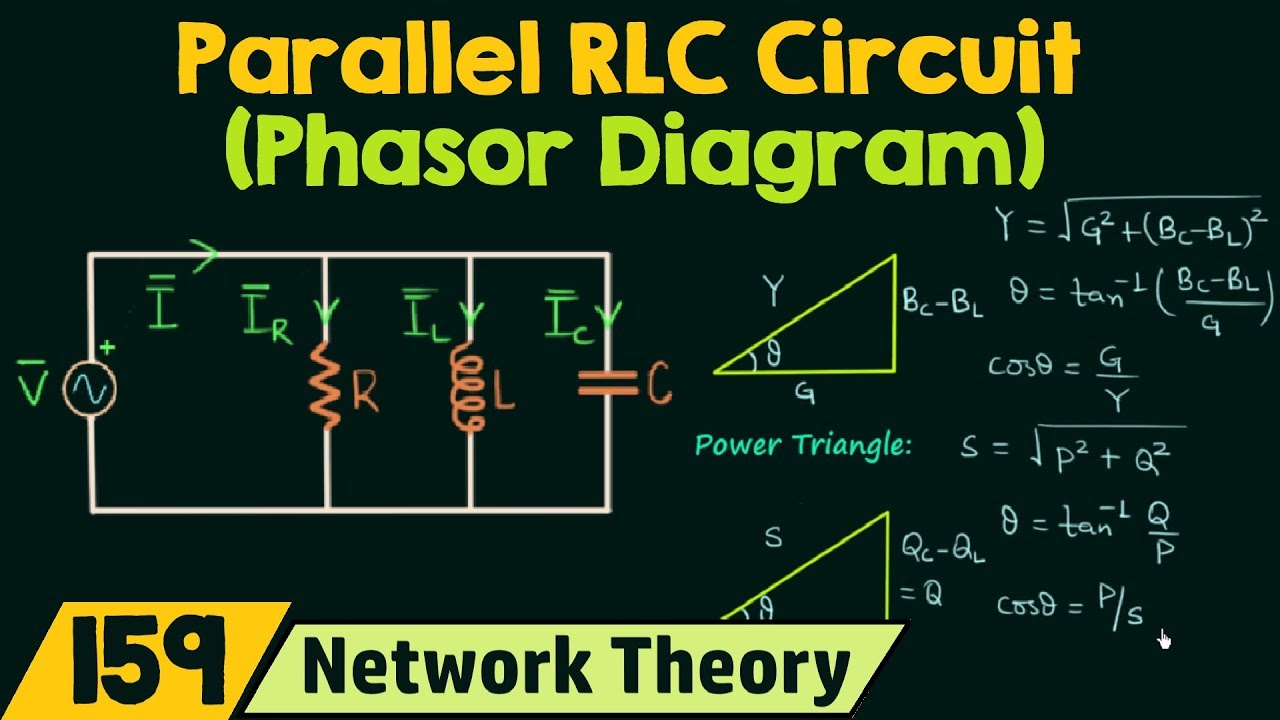
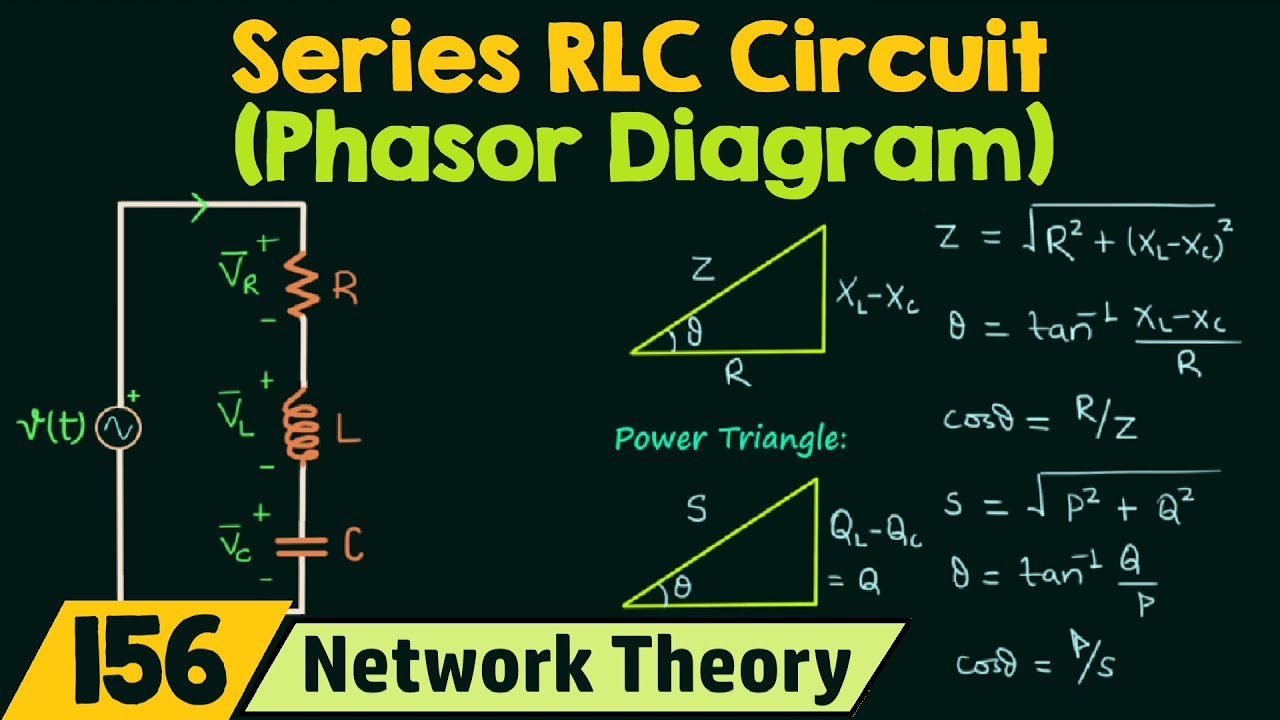
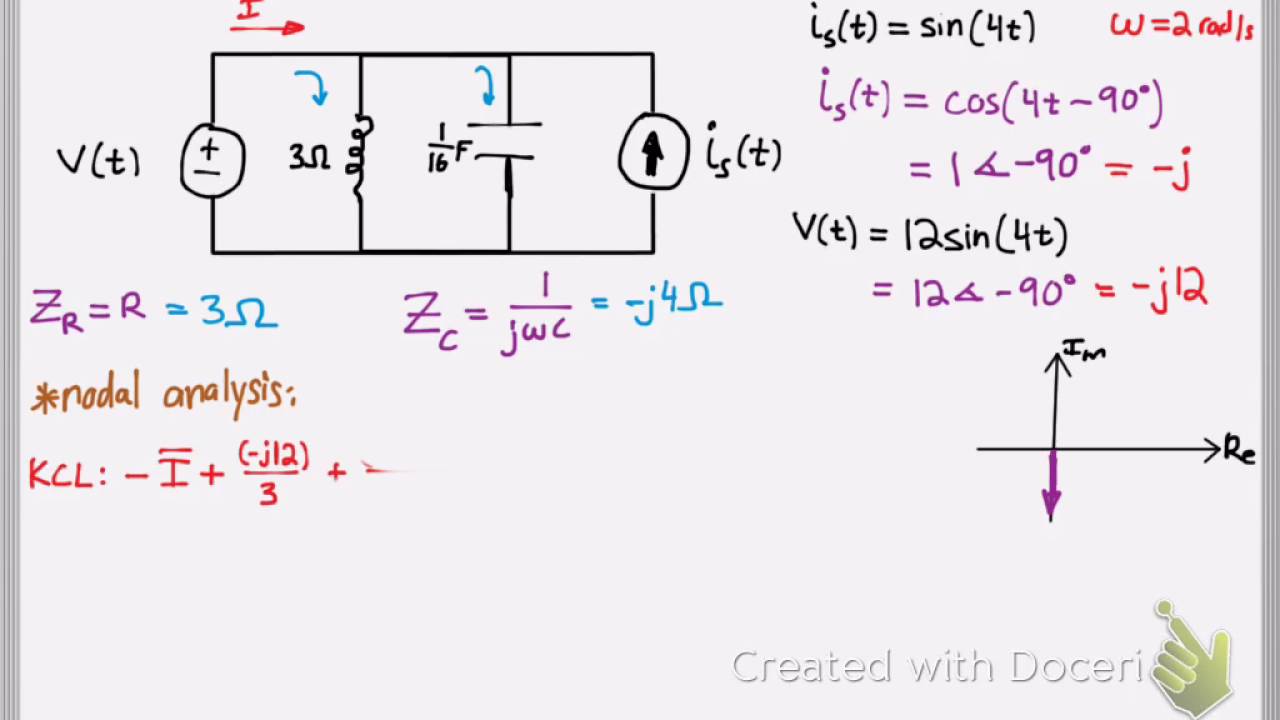
A phasor is a complex number representing the magnitude and phase of a sinusoidal voltage or current. It’s like a snapshot of the rotating vector at a specific point in time. For instance, a voltage v(t) = Vm*cos(ωt + θ) can be represented by the phasor V = Vm∠θ, where Vm is the magnitude and θ is the phase angle.
Benefits of phasor domain calculations include simplified circuit analysis, easier impedance calculations, and facilitation of power calculations in AC circuits. For example, finding the total voltage across two series components involves simply adding the respective phasor voltages.
To calculate phasor domain voltages, convert sinusoidal voltages into phasor form. Then, use phasor algebra (addition, subtraction, multiplication, division) to perform circuit analysis. Finally, convert the results back to the time domain if needed.
Advantages and Disadvantages of Phasor Domain Calculations
| Advantages | Disadvantages |
|---|---|
| Simplified analysis of AC circuits | Not applicable to non-sinusoidal waveforms |
| Easier impedance calculations | Requires understanding of complex numbers |
| Facilitates power calculations | Initial conversion to phasor domain can be time-consuming for complex circuits |
Best Practices:
1. Always ensure consistent units.
2. Double-check phase angles.
3. Use appropriate software tools for complex circuits.
4. Understand the underlying concepts of phasor representation.
5. Practice with various circuit examples.
FAQ:
1. What is a phasor? (A: A complex number representing a sinusoidal quantity.)
2. Why use phasors? (A: To simplify AC circuit analysis.)
3. How do you convert to phasor domain? (A: Use the magnitude and phase angle of the sinusoid.)
4. How do you convert back to time domain? (A: Use the inverse phasor transformation.)
5. What is impedance in phasor domain? (A: A complex number representing the opposition to current flow.)
6. How do you calculate power in phasor domain? (A: Use the phasor voltage and current.)
7. What are the limitations of phasor analysis? (A: Primarily applicable to sinusoidal steady-state conditions.)
8. Where can I find more resources on phasors? (A: Textbooks on circuit analysis, online tutorials, and educational software.)
In conclusion, mastering phasor domain voltage calculations is like gaining a superpower in the world of AC circuits. It simplifies analysis, enables efficient calculations, and unlocks a deeper understanding of how these circuits behave. By embracing this powerful tool, you can confidently navigate the intricate world of alternating currents and unlock the potential of electronic design and analysis. Start exploring the world of phasors today, and you'll find that the once-daunting realm of AC circuits becomes much clearer and more manageable. Remember to practice with different examples and utilize available resources to solidify your understanding. This knowledge will prove invaluable in your electrical engineering journey, empowering you to design and analyze complex circuits with confidence.
Solved Draw the frequency domain circuit and calculate the - Trees By Bike
Solved Convert The Phasor V 5 J3 To Time Domain Expre - Trees By Bike
Onda sinusoidal de muestra duplicado - Trees By Bike
Solved Derive and calculate voltages in the phasor domain - Trees By Bike
Solved The Phasor Learning Goal To use the phasor transform - Trees By Bike
Introduction to Electrical Engineering Notes - Trees By Bike
how to calculate phasor domain voltages - Trees By Bike
Inductive Circuit Phasor Diagram - Trees By Bike
Phasor Diagram 3 Phase Ac Circuit - Trees By Bike
How To Calculate Phase Angle In Rlc Circuit at Misty Holt blog - Trees By Bike
SOLVED 28 Calculate the voltages V and V2 for the circuits in Fig 15 - Trees By Bike
Ac Source In Circuit Diagram - Trees By Bike
SOLVED Consider the three - Trees By Bike
how to calculate phasor domain voltages - Trees By Bike
SOLVED Where f 50Hz Draw the circuit in Simulink 100 ohm 50 uF - Trees By Bike