Ever wondered how electrical engineers make sense of the swirling currents and fluctuating voltages in alternating current (AC) circuits? The answer lies in a clever graphical tool: the voltage and current phasor diagram. These diagrams transform complex sinusoidal waveforms into static vectors, making circuit analysis significantly easier.
Imagine trying to add or subtract constantly changing values. It's a bit like trying to nail jelly to a wall. Phasor diagrams provide a stable framework, allowing engineers to visualize and manipulate these oscillating quantities. They represent AC voltages and currents as rotating vectors, 'frozen' at a specific instant in time, offering a snapshot of the circuit's behavior.
The concept of representing sinusoidal quantities as vectors originated from the work of Charles Proteus Steinmetz, a pioneering electrical engineer, in the late 19th century. His insights paved the way for simplified AC circuit analysis, contributing significantly to the development of power systems we rely on today. Without phasor diagrams, understanding and designing complex AC circuits would be substantially more difficult.
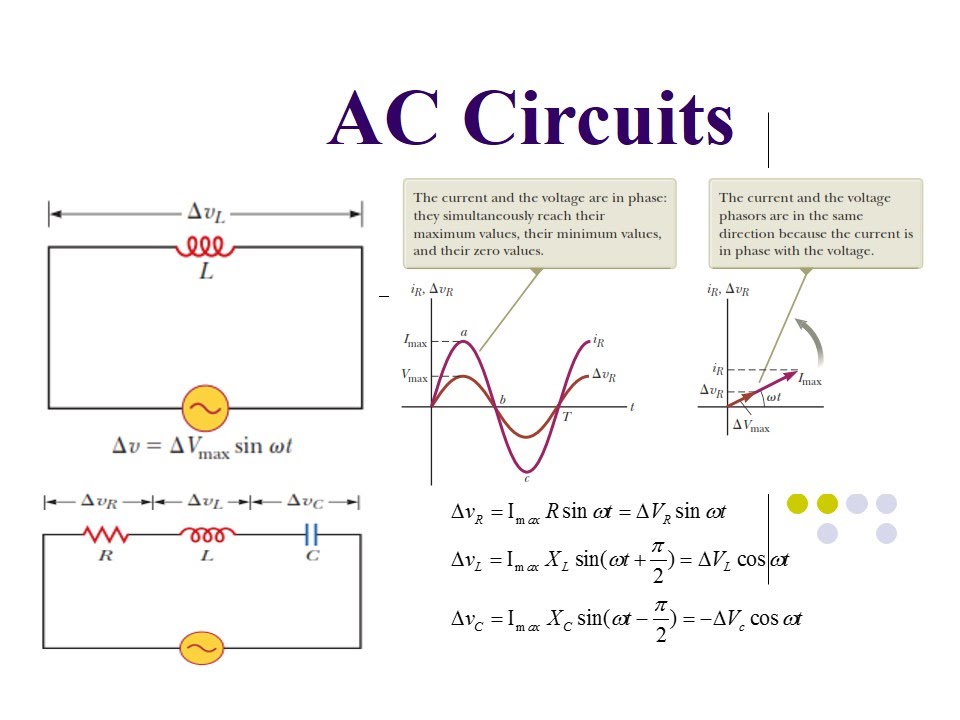
A key challenge in AC circuits lies in the phase difference between voltage and current. Unlike DC circuits where voltage and current rise and fall together, AC circuits can exhibit a time lag or lead between these two quantities. Phasor diagrams elegantly capture this phase relationship, providing a visual representation of how voltage and current are synchronized (or not) in a circuit.
Understanding voltage and current relationships is fundamental to analyzing circuit behavior. Phasor diagrams allow us to see how changes in one influence the other, providing insights into the overall circuit performance. This understanding is essential for designing and optimizing electrical systems, from simple household circuits to complex power grids.
A phasor diagram portrays AC voltage and current as vectors, whose length corresponds to the magnitude and whose angle signifies the phase. The horizontal axis typically represents the real part, while the vertical axis represents the imaginary part. This graphical representation enables us to easily perform mathematical operations like addition and subtraction on AC quantities.
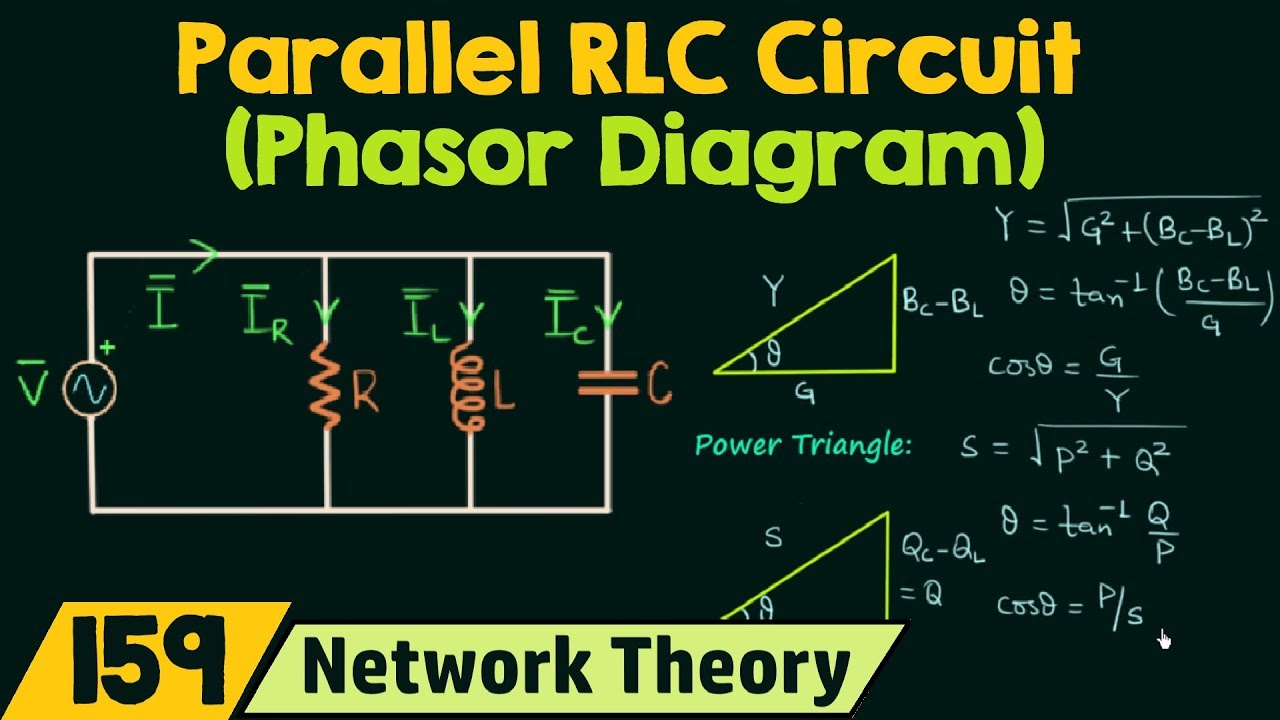
A simple example is a resistor in an AC circuit. The voltage and current phasors are aligned along the same axis, indicating zero phase difference. However, in a capacitor, the current phasor leads the voltage phasor by 90 degrees, while in an inductor, the current phasor lags the voltage phasor by 90 degrees.
Three key benefits of using phasor diagrams are: Simplified Calculations: They transform complex trigonometric calculations into simpler vector operations. Visual Representation: They provide an intuitive visual representation of phase relationships and magnitudes. Improved Circuit Understanding: They facilitate deeper understanding of circuit behavior and response to different frequencies.
To construct a phasor diagram, identify the magnitudes and phase angles of the voltage and current for each component. Draw the voltage phasor as a reference, then draw the current phasor with the correct phase angle relative to the voltage phasor. For example, in a series RL circuit, the current phasor will lag the voltage phasor by an angle between 0 and 90 degrees.
Advantages and Disadvantages of Phasor Diagrams
| Advantages | Disadvantages |
|---|---|
| Simplified AC circuit analysis | Limited to sinusoidal waveforms |
| Clear visualization of phase relationships | Can become complex for very large circuits |
| Facilitates understanding of circuit behavior | Requires basic understanding of vector algebra |
Five best practices for using phasor diagrams include: always choose a reference phasor, maintain consistent scales for magnitude, accurately represent phase angles, label all phasors clearly, and use different colors or line styles to distinguish between voltage and current phasors.
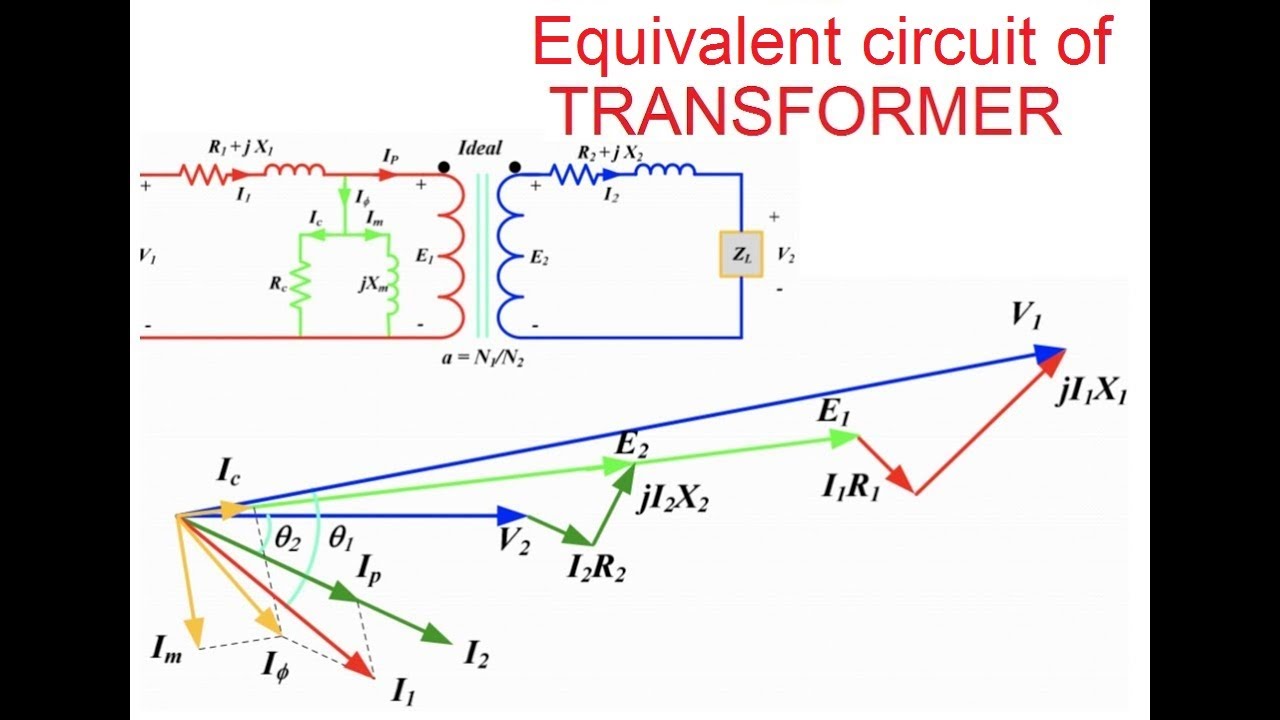
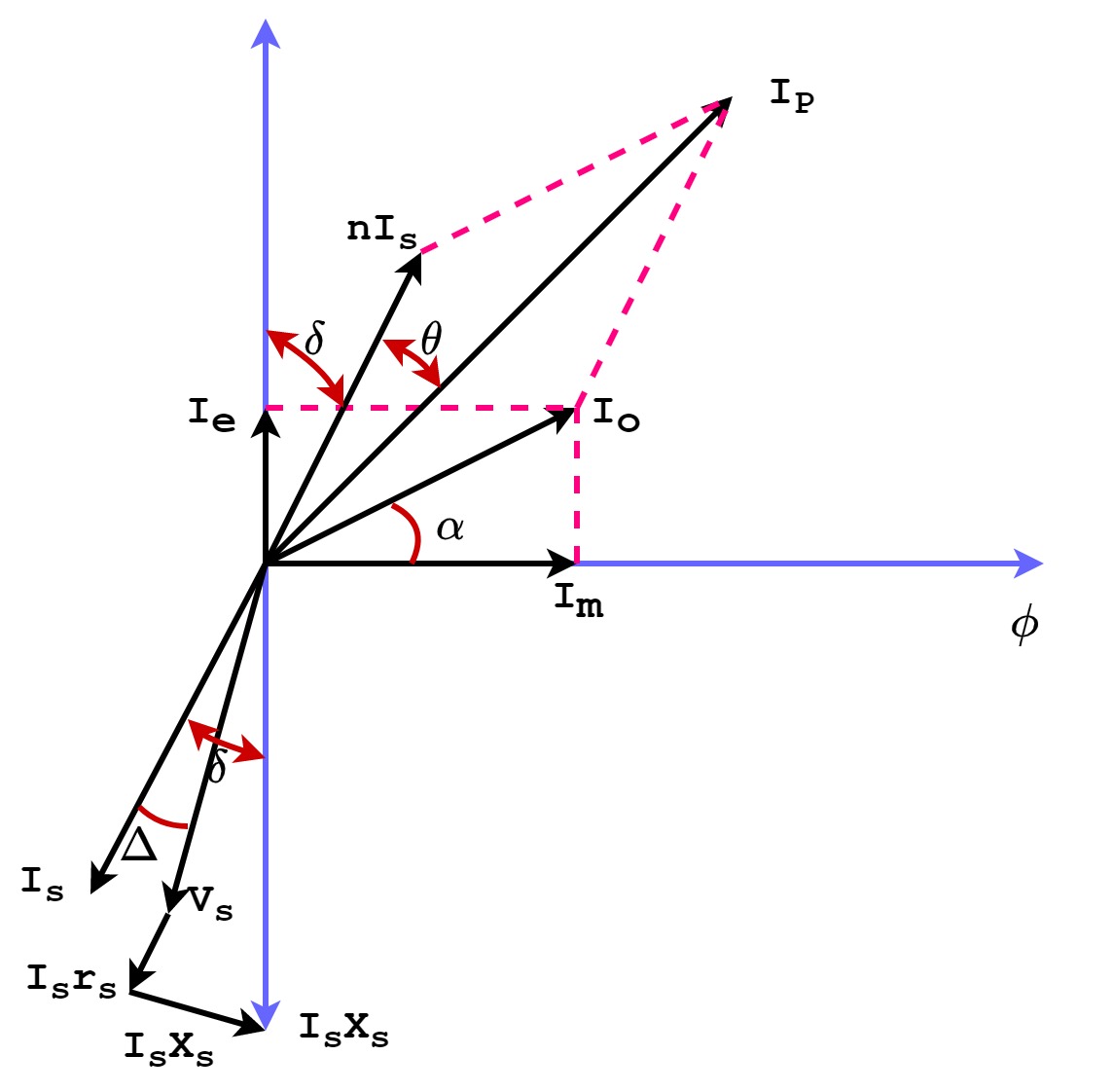
Some real-world examples of phasor diagram application include: power system analysis, motor control design, filter design, transformer analysis, and impedance matching in communication systems.
One challenge in using phasor diagrams is dealing with complex impedances. The solution is to represent impedance as a phasor with magnitude and angle. Another challenge is understanding the concept of rotating phasors. The solution is to use interactive simulations or animations to visualize the rotating vectors.
Frequently asked questions about phasor diagrams include: What is a phasor? What is the difference between a phasor and a vector? How do you draw a phasor diagram? What are the applications of phasor diagrams? How do you calculate impedance using phasor diagrams? What is the significance of phase angle in a phasor diagram? How are phasor diagrams used in power systems? How do you analyze resonant circuits using phasor diagrams?
A tip for using phasor diagrams is to always double-check the phase angles and magnitudes to ensure accuracy.
In conclusion, voltage and current phasor diagrams are indispensable tools for anyone working with AC circuits. They offer a powerful visual representation of complex relationships, simplifying analysis and design. By understanding the principles behind phasor diagrams and learning how to construct and interpret them, you unlock a deeper comprehension of AC circuit behavior. This knowledge is crucial for a wide range of applications, from designing efficient power systems to optimizing electronic devices. Explore resources online, in textbooks, and through interactive software to further enhance your understanding and mastery of phasor diagrams. Their effective utilization empowers you to tackle even the most intricate AC circuit challenges with confidence and clarity. Embracing phasor diagrams as a key analytical tool will undoubtedly strengthen your abilities in electrical engineering and related fields.
Phasor Diagram Pure Capacitive Circuit - Trees By Bike
Ac Circuit Phasor Diagram Impedance - Trees By Bike
What Voltage Does The Us Use - Trees By Bike
Phasor Diagram For Inductive Circuit - Trees By Bike
Delta Three Phase System - Trees By Bike
Draw Phasor Diagram Rlc Circuit - Trees By Bike
Phasor Diagram Of Capacitor In Ac Circuit - Trees By Bike
Equivalent Circuit Of A Single Phase Transformer - Trees By Bike
Voltage And Current Phasor Diagram - Trees By Bike
Phasor Diagram Of Rlc Series Circuit - Trees By Bike
How To Draw A Phasor Diagram For 3 - Trees By Bike
Phasor Diagram Of Pure Resistive Circuit - Trees By Bike
Inductive Circuit Phasor Diagram - Trees By Bike
Phasor Diagram Rlc Circuit At Resonance - Trees By Bike
Phasor diagram of line side voltage and current with balanced - Trees By Bike