Unlocking Geometry's Secrets: The Power of Points, Lines, and Planes

14 Apr 2024
us
Emil

[Telugu] Write three undefined terms of geometry.

Have you ever wondered how mathematicians build complex geometric structures? Like a majestic skyscraper that rises from a simple foundation, the entirety of geometry rests upon three fundamental building blocks: points, lines, and planes. These concepts, known as the "three undefined terms of geometry," might seem deceptively simple at first glance. After all, we interact with representations of them in our everyday lives. But delve a little deeper, and you'll discover a world of fascinating concepts and implications.

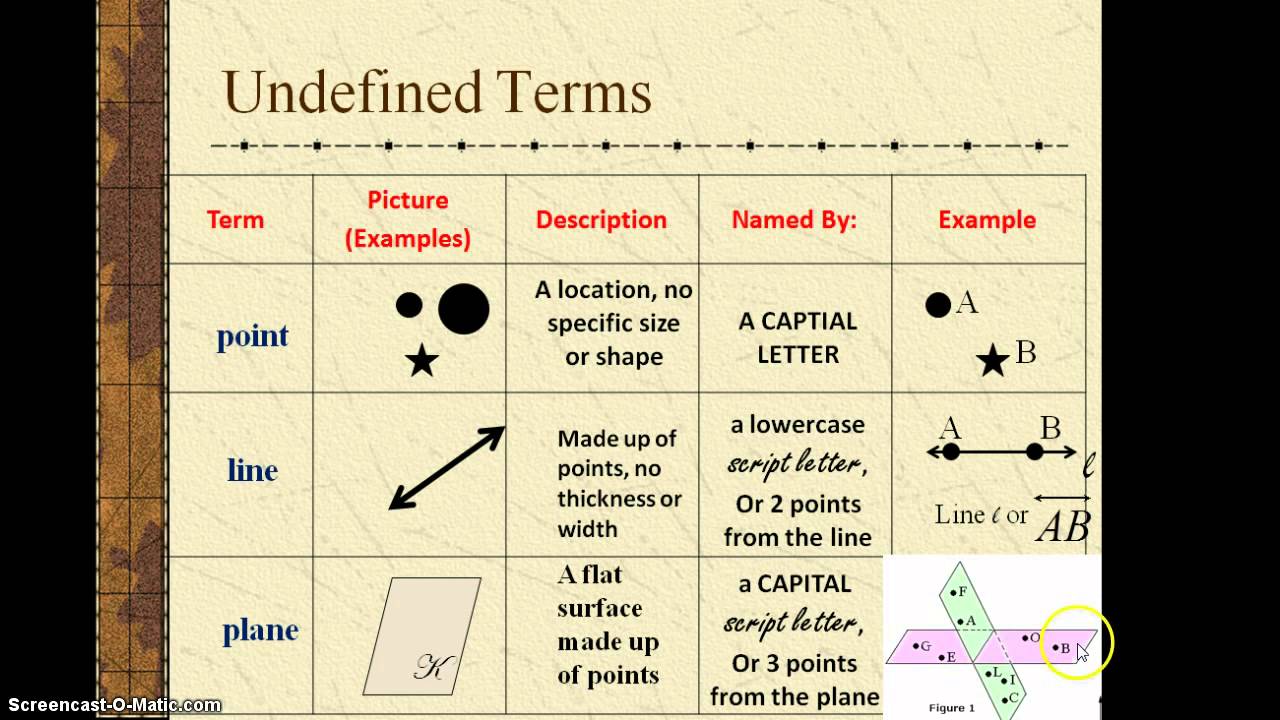
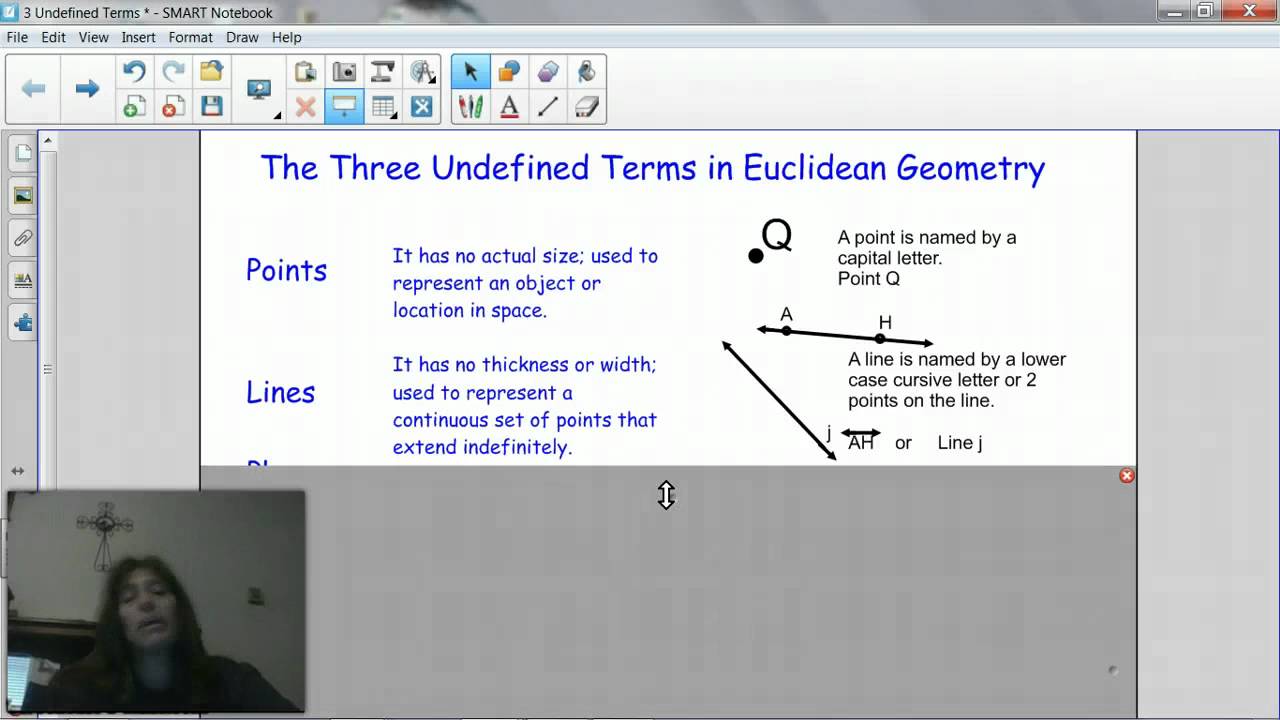
Imagine trying to describe a point. You might say it's a dot on a page or a tiny speck of dust. But can you truly define it without using other terms that themselves require definition? A point, in its purest geometric sense, is simply a location in space. It has no size, shape, or dimension – it just *is*.

Similarly, a line in geometry isn't just the straight mark you draw with a ruler. It's an infinitely extending path in one dimension, passing through an infinite number of points. It has length but no width or height.

Finally, we have the plane: a flat, two-dimensional surface that extends infinitely in all directions. Think of a tabletop that never ends, and you're getting close to the concept of a geometric plane.

These three undefined terms – point, line, and plane – form the bedrock upon which all other geometric definitions and theorems are built. They are the fundamental assumptions, the axioms upon which the entire system of Euclidean geometry is constructed.

You might wonder, why are these terms left undefined? Why not give them concrete definitions? The answer lies in the pursuit of a consistent and logical system. If we try to define a point, we'll inevitably use other terms that themselves require definition. This leads to a circular loop of definitions, ultimately resting upon some undefined terms. To avoid this, mathematicians chose these fundamental concepts as their starting point, accepting their intuitive nature without formal definition.

The importance of points, lines, and planes extends far beyond the realm of theoretical geometry. They form the basis for understanding shapes, distances, angles, and every other geometric concept. Architects use them to design buildings, engineers to build bridges, and artists to create perspective in their drawings. Our understanding of the physical world, from the smallest atom to the vast expanse of space, relies on these fundamental geometric concepts.

While points, lines, and planes might seem abstract, their implications are very real. They demonstrate the power of simple, elegant ideas to unlock complex systems. By starting with these undefined terms, geometry builds a powerful and consistent framework for understanding the world around us.

So, the next time you encounter a seemingly simple geometric shape, remember the invisible foundation upon which it stands—the intriguing world of points, lines, and planes, the undefined terms that make it all possible.